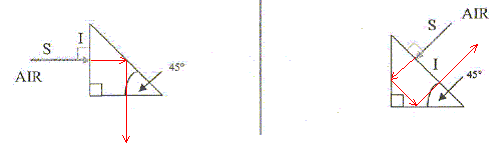réflexion et réfraction lycée En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .
optique : historique (mots croisés) voir le match : l'essentiel du cours
	calcul d'une durée en nanoseconde
Combien de temps met la lumière pour parvenir de votre livre à votre oeil ( d=25 cm) ? corrigé distance = 0,25 m vitesse de la lumière dans l'air 3 108 ms-1. durée = 0,25 / 3 108 = 8,3 10-10 s 1 nanoseconde (ns)= 10-9 s 0,83 ns
2	année lumière : distance parcourue par la lumière en 1 an
Quelle est la valeur d'une année lumière ? corrigé durée : 365*24*3600 = 3,15 107 s vitesse de la lumière dans le vide 3 108 ms-1. distance parcourue : 3,15 107 *3 108 9,46 1015 m
3	fréquence et longueur d'onde
Quelle est la fréquence d'une radiation lumineuse de longueur d'onde l=600nm ? corrigé longueur d'onde 600 10-9 m =6 10-7 m vitesse de la lumière dans le vide 3 108 ms-1. fréquence : 3 108 / 6 10-7 5 1014 Hz
4	réflexion réfraction
Dessiner le rayon réfléchi et le rayon réfracté et calculer les angles de réflexion et de réfraction corrigé angle d'incidence = angle de réflexion =30° nair sin 30 = n eau * sin i2 sin i2 = 1*0,5 / 1,33 i2 = 19,5°
5	angle limite
L'indice d'un verre est est 1,5 . Quel est la valeur de l'angle limite pour la réfraction verre-air ? corrigé Lors du passage de l'air dans le verre, le rayon réfracté existe toujours. Par contre lors du passage du verre dans l'air il existe un angle limite d'incidence au dela duquel le rayon réfracté n'existe pas: il y a réflexion totale. sin( angle limite) = 1/1,5=0,666 41,8°. Tracer la marche du rayon lumineux jusqu'à la sortie du prisme d'indice n=1,50, plongé dans l'air dans les deux cas de figure. D'une part, un faisceau perpendiculaire à la surface séparant deux milieux transparents, n'est pas dévié. D'autre part, le faisceau réfracté existe si l'angle d'incidence est inférieure à imax tel que sin imax = 1/n2 ; sin imax = 1/1,50 =0,667 soit imax =42°. Or l'angle d'incidence vaut 45°, valeur supérieure à imax : il y a réflexion totale.
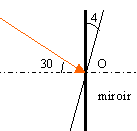
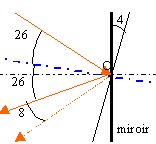
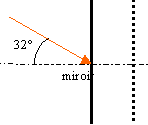
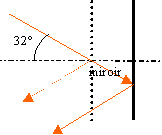
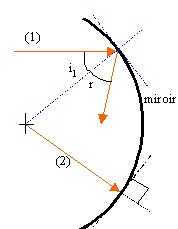
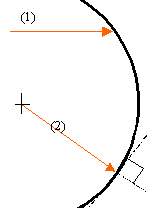
6 rotation d'un miroir On fait tourner le miroir d'un angle a=4° autour d'un axe passant par O. De quel angle le rayon réfléchi a t-il tourné ? corrigé le nouvel angle d'incidence vaut 26° ainsi que le nouvel angle de réflexion 7 translation d'un miroir On déplace le miroir de 5 cm parallèlement à lui même. Dessiner le nouveau rayon réfléchi. A t-il tourné ? corrigé 8 miroir sphérique construire les rayons réfléchi correspondant aux deux rayons incidents. (2) passe par le centre de la sphère. corrigé au point de tangence rayon et tangente sont perpendiculaires. rayon(2) perpendiculaire à la surface du miroir(angle d'incidence i1=0) le rayon réfléchi est confondu avec le rayon incident. 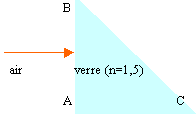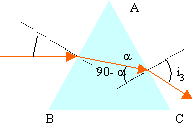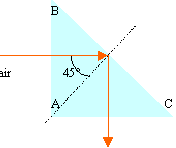rayon(1): les angles i1 et r sont égaux 9 la section du prisme est un triangle rectangle isocèle dessiner la marche ultérieure du rayon incident corrigé faces AB et AC: le rayon est perpendiculaire à la face donc pas de déviation face BC : l'angle d'incidence est supérieur à l'angle limite (41,8° pour verre-air) donc réflexion totale. 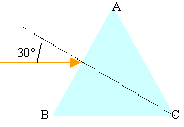10 la section du prisme est un triangle équilatéral L'indice de réfraction du prisme est 1,5. Dessiner les rayons obtenus par réfraction sur les 2 faces AB et AC et calculer l'angle du rayon émergent avec la normale à la face AC. 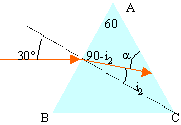corrigé sin(30)=1,5 sin(i2) d'où i2= 19,5° et a=49,5° 1,5 sin(90-49,5)= sin(i3) d'où i3= 77° 11 Un rayon monochromatique arrive sur une vitre faite de verre d'indice n=1,5 et d'une épaisseur e =5 mm. L'angle d'incidence est i =30°. Calculer l'angle de réfraction du rayon dans le verre puis tracer ce rayon. Calculer l'angle d'incidence de ce rayon sur le dioptre verre/air. Avec quel angle de réfraction le rayon émerge t il de la vitre ? Tracer ce rayon émergent. Comparer la direction du rayon qui arrive sur la vitre et celle de celui qui en sort. Cela dépend il de la valeur de l'indice n ? Le rayon lumineux incident est de couleur blanche. Comment seront les rayons des différentes couleurs à la sortie de la vitre ? Comparer l'effet d'un prisme et l'effet d'une vitre sur la lumière blanche. 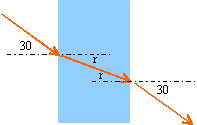corrigé 1 sin 30 = 1,5 sin r sin r = 0,333 d'où r = 19,47° puis dioptre verre air : angle d'incidence 19,47 ° (angle alterne interne) 1,5 sin 19,47 = 1 sin i' i' = 30° le rayon incident et le rayon émergeant ont des directions parallèles quel que soit l'indice n donc pas de dispersion de la lumière blanche par la vitre. par contre dans un prisme il y a dispersion de la lumière blanche, car la longueur d'onde de la lumière dépend de l'indice n. Le prisme est un milieu dispersif. 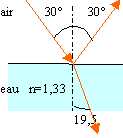12 Un disque opaque de diametre D =10cm flotte, immobile, à la surface de l'eau d'un cristallisoir. La hauteur d'eau est H=20cm. L'indice de l'eau est n=1,33. Un oeil est placé en O à la vertical du centre du disque et à une distance h=10cm au dessus de celui-ci. Quelle est la forme de la partie du fond du cristallisoir qui sera masquée par le disque ? Calculer l'angle de réfraction r de ce rayon dans l'air; en déduire l'angle d'indice i dans l'eau. Calculer le diamètre de la partie du fond invisible à partir du point O. 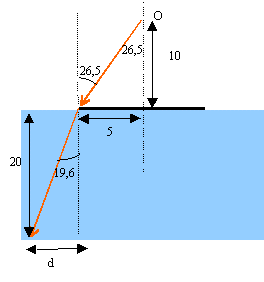corrigé tan r = 5/ 10 =0,5 d'où r =26,5° loi de Descartes concernant la réfraction : 1 sin 26,5 = 1,33 sin i sin i = 0,336 et i = 19,6 ° rayon du cercle sur le fond du cristallisoir : tan 19,6 = d / 20 d'où d = 0,356 *20 = 7,13 cm puis 5 + 7,13 =12,1 cm. 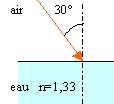On réalise un montage comportant 2 miroirs plans formant un dièdre d'angle 45°. On fait alors tomber un rayon sous incidence a sur le montage. Calculer l'angle de déviation entre le rayon incident et le rayon émergent. 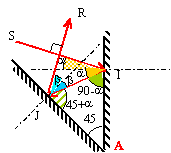en I l'angle d'incidence a est égal à l'angle de réflexion. Dans le triangle AIJ , l'angle( JI ; JA) vaut : 180-45-(90-a) = 45 + a. l'angle d'incidence en J sur le second miroir est b soit 45-a. en J l'angle d'incidence 45-a est égal à l'angle de réflexion. Le premier miroir introduit une déviation égale à 2 a Le second miroir introduit une déviation égale à 2*(45-a) = 90-2a soit une déviation totale de 90°.   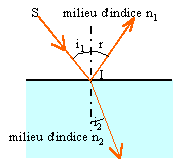Lorsque la lumière traverse la surface séparant deux milieux transparents, elle subit un changement de direction. Comment appelle-t-on ce phénomène ? Citer deux milieux transparents. On dirige un faisceau lumineux monochromatique issu d'un laser vers la surface plane d'un demi-cylindre en Plexiglas. On mesure les angles i1 et i2 appelés respectivement angle d'incidence et angle de réfraction. Définir le terme monochromatique. Faire un schéma en faisant apparaître les angles i1 et i2. On souhaite montrer que la loi qui donne l'angle de réfraction i2 en fonction de i1 est donnée par la relation suivante : n1.sin i1=n2.sin i2 (1). En faisant varier l'angle d'incidence i1, on obtient le tableau 1 : i1 0 10 20 30 40 50 60 70 i2 0 7 13 20 25 30 35 38 sin i1 sin i2 - Quel est le nom de cette loi ? (elle porte le même nom que le physicien qui l'a découverte). - Quel est le nom des constantes n1 et n2 qui apparaissent dans l'expression (1) ? - Dans notre cas d'étude, n1=1. Quel est le milieu 1 ? Comment se simplifie l'expression (1) ? - Compléter le tableau 1. Construire la courbe sin i1=f(sin i2). On placera sin i1 en ordonnée (verticale), sin i2 en abscisse (horizontale) puis on prendra la même échelle sur les 2 axes : 1 cm pour 0,1. En déduire, à l'aide du graphique, le coefficient directeur puis l'équation de la droite obtenue. Que vaut n2 ? Déterminer graphiquement l'angle de réfraction i2 pour un angle d'incidence i1=35°. La lumière se propage dans le Plexiglas à la vitesse v. - Quelle relation peut-on écrire entre n2 et v ? - Calculer v. On donne la vitesse de propagation de la lumière dans le vide: c=3.108 m.s-1 et n2=1,5. Qu'est ce qu'une lumière blanche ? - Donner le matériel nécessaire pour obtenir le spectre de la lumière blanche. Qualifier le spectre. - Dessiner le spectre obtenu. - Indiquer les longueurs d'onde et les couleurs des extrémités du spectre. corrigé Lorsque la lumière traverse la surface séparant deux milieux transparents, elle subit un changement de direction, appelé réfraction. Deux milieux transparents : l'air, l'eau, le verre. monochromatique : une seule couleur donc une seule fréquence pour la radiation. nom de cette loi : Descartes nom des constantes n1 et n2 : indice de réfraction du milieu transparent. pour l'air n1=1 et la loi de Descates s'écrit : sin i1=n2.sin i2 . 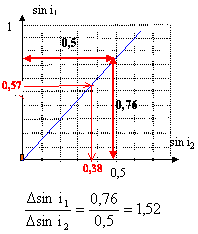i1 0 10 20 30 40 50 60 70 i2 0 7 13 20 25 30 35 38 sin i1 0 0,173 0,342 0,5 0,643 0,766 0,866 0,94 sin i2 0 0,122 0,225 0,342 0,422 0,5 0,573 0,616 graphiquement la pente de la droite donne n2 = 1,52. angle de réfraction i2 pour un angle d'incidence i1=35° sin i1 =sin 35 =0,574 ; le graphe indique : sin i2 =0,38 soit i2 =sin-1(0,38) = 22°. La lumière se propage dans le Plexiglas à la vitesse v = c/n2 = 3 108 / 1,5 = 2 108 m/s. Une lumière blanche est une lumière polychromatique contenant toutes les couleurs de l'arc en ciel. matériel nécessaire pour obtenir le spectre de la lumière blanche : rétroprojecteur + réseau + écran. longueurs d'onde et les couleurs des extrémités du spectre : 400 nm à la limite du violet et des ultra-violet et 780 nm à la limite du rouge et des infra-rouge. Un pinceau de lumière blanche arrive sous l'angle d'incidence i = 50° à la surface de séparation plane de l'air et du verre. indice de réfraction du verre pour le bleu nB= 1,524 ; pour le rouge nR = 1,515. 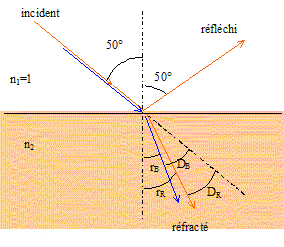D'une part, pour le faisceau bleu : sin 50 = nB sin rB soit sin rB = sin 50 / nB = sin 50 / 1,524 =0,5026 ; rB =30,17° ; DB=50-30,17 = 19,83° D'autre part, pour le faisceau rouge : sin 50 = nR sin rR soit sin rR = sin 50 / nR = sin 50 / 1,515 =0,5056 ; rR =30,37° ; DR=50-30,37 = 19,63° Valeur de l'angle entre deux rayons, un bleu et un rouge, transmis par le verre : 30,37-30,17 = 0,2°. Le rayon bleu subit la plus grande déviation. On considère le dispositif ci-dessous. L'écran d'observation est à la distance D=2 m de l'ouverture circulaire de rayon a = 0,05 mm. Le dispositif est éclairé par une radiation de longueur d'onde l0 = 632 nm. 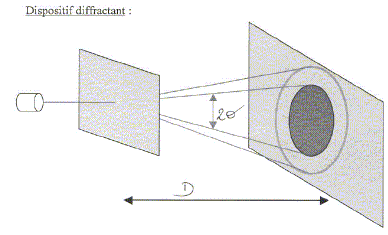Calcul les rayons des premiers maxima et minima de lumière sachant que l'angle q est donné par les formules : centre 1er minimum 2ème maximum 3ème maximum sin q 0 0,61 l0/a = 7,7 10-3 0,82 l0/a= 1,036 10-2 1,11 l0/a =1,40 10-2 q (radian) 0 7,7 10-3 1,036 10-2 1,40 10-2 r = D q = 2 q avec q en radian 0 1,54 10-2 m = 1,54 cm 2,07 10-2 m = 2,07 cm 2,80 10-2m = 2,8 cm l0 = 632 10-9 m ; a = 0,05 mm = 5 10-5 m ; l0/a =0,0126 . retour - menu