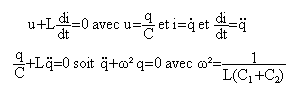Aurelie fév 2001

. .
circuit LC libre non amorti

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

1

charge et intensité en fonction du temps

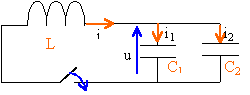
On considère le circuit ci-dessus les condensateurs portent les charges qo1 et qo2 lorsque l'interrupteur est ouvert .

  1. Comparer les charges qo1 et qo2 des deux condensateurs.
  2. On ferme l' intérupteur .Etablir :
  • la loi d' évolution, en fonction du temps, de la charge de chacun des condensateurs.
  • la loi d'évolution en fonction du temps , de l' intensité qui passe dans chacune des 3 branches du circuit.
corrigé


les armatures des condensateurs reliés par un fil de cuivre portent des charges identiques au départ lorsque l'interrupteur est ouvert. On note q0 cette charge initiale portée par chaque condensateur.

les deux condensateurs sont en parallèles, on peut les remplacer par un condensateur unique de capacité C = C1+C2

le circuit se simplifie bobine en série avec le condensateur unique de capacité C, interrupteur fermé.

solution q= q0 cos (w t)

puis écrire que la tension aux bornes des condensateurs est u = q / (C1+C2)

u = q0 / (C1+C2) cos (w t)

puis q1 = C1 u et q2 = C2 u

quand aux intensités i1 et i2 dériver la charge par rapport au temps

(cos (wt) )' = -w sin(wt)

i = i1 + i2 = -w q0 sin (wt)

retour - menu