|
.
. |
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|
|
|
|
|
|
rappels mathématiques |
On considère l'intégrale suivante : 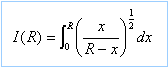
|
|
|
|
|
|
|
gravitation |
On suppose que le mouvement de la terre de masse m autour du soleil est un mouvement circulaire uniforme de rayon R, de vitesse v0. Terre et Soleil sont assimilés à des points matériels.
corrigé |
|
|
|
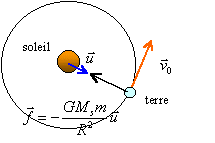
l'accélération est centripète de norme aN= v0² / R la seconde loi de newton s'écrit :
|
|
|
aspect énergétique de la chute |
On imagine que la vitesse de la terre s'annule brusquement. Celle ci soumise uniquement à la force de gravitation exercée par le soleil va donc finir par tomber sur le soleil. La terre décrit une trajectoire rectiligne et on se propose de déterminer la durée de la chute, tout frottement étant négligé.
corrigé |
|
|
|
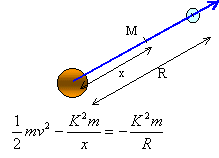
|
|
|
équation différentielle et son intégration |
corrigé |
|
|
|
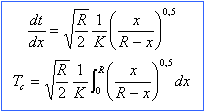
|

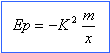 où
K est une constante positive. Exprimer l'énergie
mécanique de la terre.
où
K est une constante positive. Exprimer l'énergie
mécanique de la terre.