Mathématiques,
fonctions
Bac St2S 2013.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie.
Un
médicament est administré en intraveineuse. Un laboratoire étudie le
processus d’absorption de ce médicament par l’organisme pendant les 12
heures qui suivent l’injection.
La quantité de produit présent dans le sang est exprimée en cm3.
Le temps t est exprimé en heures. La quantité de produit présent dans
le sang, en fonction du temps t , est donnée par f (t ) = 4×0,85t
où t désigne un nombre réel appartenant à l’intervalle [0 ;12 ].
Partie A.
1. Calculer la
quantité de produit présent dans le sang à l’instant t = 0 .
f(0) = 4 x0,850 = 4 cm3.
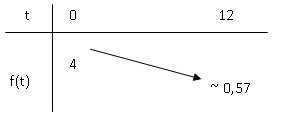
2. On admet que la
fonction f a les mêmes variations sur l’intervalle [0 ; 12] que la
fonction g définie sur l’intervalle [0 ; 12] par g (t )= 0,85t
. Établir le tableau des variations de f sur l’intervalle [0 ; 12].
Si 0 < a <1, la fonction h(x) = ax est strictement
décroissante sur R. La fonction f(t )=4 x 0,85t
est strictement décroissante sur [0 ; 12 ].
3. Résoudre
l’équation f (t ) = 1.On donnera la valeur exacte de la solution puis
une valeur approchée au dixième.
1 = 4 x0,85t ; ln(1) =ln(4)+ t ln(0,85) ; 0 = ln(4)+
t ln(0,85) ; t = - ln(4) / ln(0,85)
~8,5 heures.
Partie B.
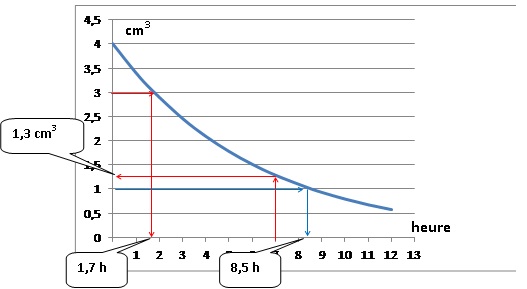
On a représenté ci-dessous la courbe Cf représentative de
la fonction f.
1. Déterminer
graphiquement la quantité de produit présent dans le sang au bout de 7
heures.
2. Déterminer
graphiquement au bout de combien de temps la quantité de produit
présent dans le sang aura diminué de 25%.
3. Le laboratoire
indique que le médicament n’est plus efficace lorsque la quantité de
produit présent
dans le sang est inférieure à 1 cm3. Déterminer
graphiquement la durée d’efficacité de ce médicament.
|
|
|
Antilles.
Un
laboratoire pharmaceutique fabrique et commercialise un vaccin. Sa
capacité de production, sur une semaine, lui permet de réaliser entre 0
et 18 litres de ce produit. On note B(x) le bénéfice hebdomadaire (en
euros) réalisé par le laboratoire pour une production d’un volume x de
vaccin exprimé en litres. On appelle B la fonction définie pour tout x
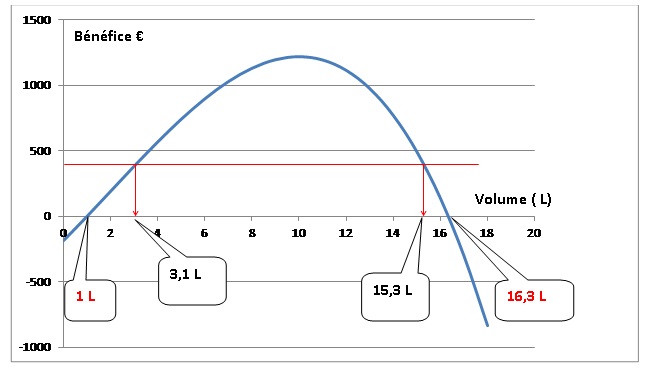
de l’intervalle [0 ; 18] qui à x associe B(x). La courbe représentative
de la fonction B est donnée.
Partie A : Lecture
graphique
1. Déterminer à
l’aide du graphique le(s) volume(s) hebdomadaire(s) nécessaire( s) pour
que le bénéfice hebdomadaire soit égal à 400 euros.
2. Déterminer à
l’aide du graphique pour quels volumes hebdomadaires produits, le
laboratoire est bénéficiaire.
Partie B. Étude du
bénéfice hebdomadaire
On admet que B est la fonction définie pour tout nombre réel x de
l’intervalle [0 ; 18] par :
B(x) = −x3 +6x2 +180x −184.
On notera B′ la fonction dérivée de la fonction B.
1. a. Déterminer
pour tout x appartenant à l’intervalle [0 ; 18], l’expression de B′(x).
B'(x) = -3x2
+12x+180.
b. Vérifier que,
pour tout x appartenant à l’intervalle [0 ; 18], B′(x) = (−3x +30)(x
+6).
B'(x) = -3x2 -18x +30x +180 = -3x2 +12x +180.
c.
Étudier le signe de B′(x) pour tout x appartenant à l’intervalle [0 ;
18].
d. En déduire le
tableau de variations de la fonction B sur l’intervalle [0 ; 18].
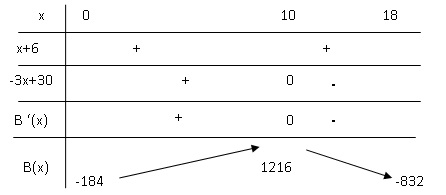
2. Déterminer le
volume hebdomadaire à produire pour obtenir un bénéfice maximal. 10 L.
Quel est le montant, en euros, du bénéfice hebdomadaire maximal ? 1216 €.
|
|
|
|
Métropole.
Pour
traiter un patient, un médecin procède à l’injection intramusculaire
d’une dose d’une substance médicamenteuse au temps t = 0 (t est exprimé
en heures). Le produit actif se diffuse dans le sang puis est
progressivement éliminé.
Le médicament est efficace lorsque la concentration du produit actif
dans le sang est supérieur ou égale à 25 mg.L−1 (25
milligrammes par litre).
La concentration maximale du produit actif dans le sang ne peut pas
dépasser 40 mg.L−1 pour éviter les effets secondaires.
Partie A : Étude
graphique
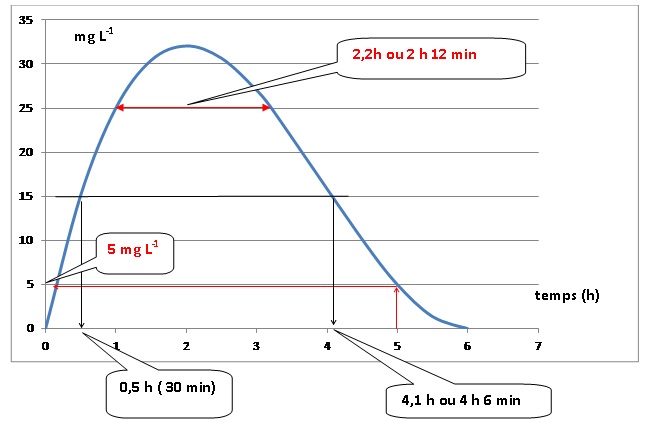
La courbe donnée représente la concentration en mg.L−1
du produit actif dans le sang du malade en fonction du temps écoulé
depuis l’injection du médicament. À l’aide de cette courbe répondre,
avec la précision que permet le graphique, aux questions suivantes en
faisant apparaître les traits de constructions utiles.
1. Déterminer la
concentration en mg.L−1 du produit actif pout t = 5. 5 mg L-1.
2. Le médecin
a-t-il respecté la dose à ne pas dépasser ? Expliquer.
Oui, car le maximum de la courbe est inférieur à 40 mg / L.
3. Déterminer les
temps en heures et minutes pour lesquelles la quantité de produit actif
est de 15 mg.L−1.
4. Quelle est la
durée pendant laquelle le médicament est resté efficace ?
5. Au bout de
quelle durée le médicament est-il complètement éliminé ? 6 heures.
Partie B : Étude
numérique
On admet que la concentration, exprimée en mg.L−1, du
produit actif dans le sang dumalade est donnée en fonction du temps t ,
exprimé en heures, par la fonction f définie sur l’intervalle [0 ; 6]
par :
f (t )= t 3−12t 2 +36t .
1. Reproduire et
compléter le tableau de valeur numérique.
t
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
f(t)
|
0
|
25
|
32
|
27
|
16
|
5
|
0
|
2. a. On note f ′
la fonction dérivée de la fonction f sur l’intervalle [0 ; 6]. Calculer
f ′(t ).
f '(t) = 3t2
-24t+36.
b. Démontrer que,
pour tout nombre réel t de l’intervalle [0 ; 6], on a : f ′(t ) = (t
−6)(3t −6).
(t −6)(3t −6) =3t2-18t -6t+36 = 3t2-24t+36 = f
'(t).
c. Résoudre
l’équation f ′(t ) = 0 sur l’intervalle [0 ; 6].
t-6 = 0 soit t = 6 ; 3t-6 = 0
soit t = 2.
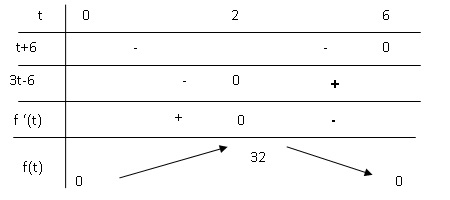
3. a. Étudier le
signe de f ′(t ) sur l’intervalle [0 ; 6].
b. Construire le
tableau de variations de la fonction f sur l’intervalle [0 ; 6].Partie B
En France, à la fin de l’année 2005, on comptait 940 éoliennes. Depuis,
chaque année,
500 éoliennes supplémentaires ont été installées. On note, pour tout
entier naturel
n, un le nombre d’éoliennes présentes en France à la fin de l’année
(2005+n).
On a donc u0 = 940.
1. Déterminer la nature de la suite (un). On précisera sa raison.
2. Exprimer un en fonction de n.
3. Combien d’éoliennes y aura-t-il en France à la fin de l’année 2013 ?
En déduire la concentration maximale du produit actif dans le sang du
malade.
|
|
Polynésie septembre.
On étudie l’évolution, en fonction du temps,
d’une population de levures présentes dans un milieu liquide.
Partie A.
Entre 0 et 300 minutes, on admet que le nombre N de levures de
l’échantillon en fonction du temps t (en minutes) est donné par :
N(t )= 150×1,01t .
1. Calculer le
nombre de levures à l’instant initial.
N(t=0) = 150 x1,010 = 150.
2. Donner, en le
justifiant, le sens de variation de la fonction f définie sur
l’intervalle [0 ; 300] par f (t ) = 1,01t .
Si a >1, la fonction at est strictement croissante sur
R. f (t ) = 1,01t est
strictement croissante sur [0 ; 300 ].
On admet que la fonction N a
les mêmes variations sur l’intervalle [0 ; 300] que la fonction f .
3. Recopier et
compléter le tableau de valeurs suivant. (Arrondir les résultats à
l’unité)
t
|
0
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
N(t)
|
150
|
166
|
183
|
202
|
223
|
247
|
273
|
301
|
333
|
367
|
406
|
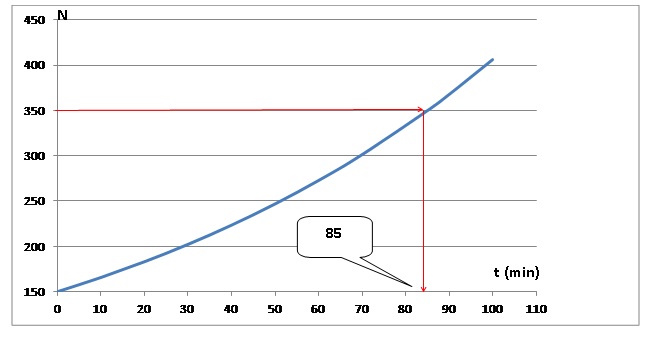
4. Dans un repère
orthogonal, représenter graphiquement la fonction N sur l’intervalle [0
; 100].
5. Déterminer
graphiquement au bout de combien de temps le nombre de levures est égal
à 350.
6. Déterminer, par
le calcul, au bout de combien de temps le nombre de levures devient
supérieur à 1000. On arrondira le résultat à la minute.
1000 = 150 x1,01t ; 1000 / 150 = 1,01t ; log(1000
/ 150) = t log (1,01 ) ; t = log(1000
/ 150) / log (1,01 ) ~191 min.
Partie B.
Au bout de 300 minutes le nombre de levures est stationnaire pendant 30
minutes, puis il peut être modélisé par la fonction g définie sur
l’intervalle [330 ; 480] par
g (t )= 0,0056t 2 −6,1517t +4389, t étant exprimé en minutes.
1. Calculer g ′(t
), où g ′ désigne la fonction dérivée de la fonction g .
g'(t) = 2 x0,0056t -6,1517 = 0,0112t
-6,1517.
2. Étudier le signe
de g ′(t ) et en déduire le tableau de variation de la fonction g.
g'(t)=0 si t = 6,1517 / 0,0112 ~549.
g'(t) < 0 si t <549 ; g'(t) >0 si t >549.
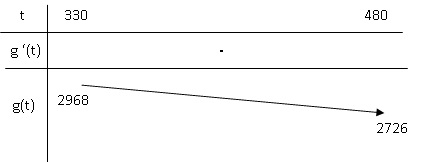
3. Comment évolue
le nombre de levures sur l’intervalle [330 ; 480] ?
Le nombre de levures est strictement décroissant sur [330 ; 480].
Quel est le nombre de levures au bout de 8 heures ? On arrondira le
résultat à l’unité.
8 h = 8 x60 = 480 min ; N = 2726.
Métropole septembre.
Partie A.
On considère la fonction f définie sur l’intervalle [−5 ; 10] dont la
représentation graphique C est donnée dans le repère orthonormal
ci-dessous. La droite (D) est
tangente à la courbe au point A d’abscisse 5.
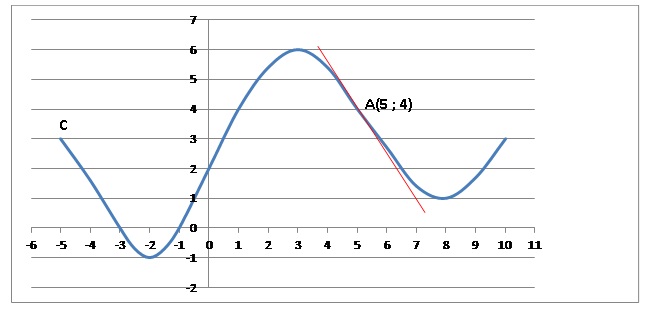
1. L’ensemble des
solutions de l’inéquation f (x)>0
est :
a. [0 ; 10] ; b. [−5 ; −3] union [−1 ; 10], vrai ; c. [−2 ; 3] union [8 ; 10].
2. L’ensemble des
solutions de l’équation f (x) = 0 est :
a. {2} ; b. {−3 ; −1}, vrai
; c. {−2 ; 3 ; 8}.
3. Le nombre dérivé
de la fonction f en x = 5 est égal à :
a. 5 ; b. −3 / 2 , vrai ; c.
−2.
La tangente en A a un coefficient directeur négatif.
Partie B.
On considère la fonction g définie sur l’intervalle [0 ; +1[ par g (x)
= 2500*0,7x .
1. L’image,
arrondie à l’unité, de 5 par la fonction g est égale à :
a. 420 ; b. 8 750 ; c. 7 500.
2500 x0,75 ~ 420.
2. Les solutions de
l’inéquation g (x)< 100 sont les nombres réels x tels que :
a. x >log(0,04) / log(0,7), vrai
; b. x < log(0,04) / log(0,7) ; c. x < log(0,7) /log(0,04).
2500*0,7x
< 100 ; 0,7x <100 /2500 ; 0,7x <0,04 ; x log (0,7) <log
(0,04).
log (0,7) et log (0,04) sont négatifs.
x > log (0,04) / log (0,7).
Antilles septembre.
En médecine, le taux
d’hématocrite est le rapport du volume des globules rouges circulant
dans le sang sur le volume total de sang. Chez l’homme, la valeur est
normale
si ce taux est compris entre 0,4 et 0,52.
1. Un patient
arrive en urgence à l’hôpital et on mesure son taux d’hématocrite qui
vaut 0,36.
Pour augmenter ce taux, on lui injecte un médicament. On contrôle
régulièrement son taux d’hématocrite pendant les huit premières heures.
On définit
sur l’intervalle [0 ; 8] la fonction f , qui à t , la durée écoulée en
heures depuis la prise du médicament, associe le taux d’hématocrite du
patient. La fonction
f est représentée.
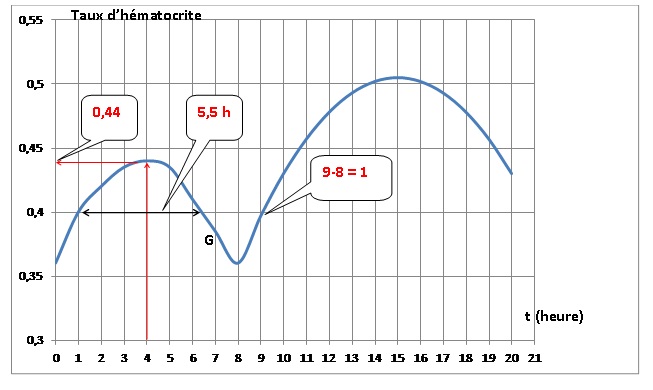
En utilisant le graphique, répondre aux questions suivantes :
a. Quelle durée se
sera écoulée depuis la prise du médicament pour avoir un taux
d’hématocrite maximal ? Quel est alors ce taux ?
Au bout de 4 heures le taux
est maximum et vaut 0,44.
b. Pour quelles
valeurs de t dans l’intervalle [0 ; 8], le taux d’hématocrite du
patient est-il normal ? [1 ; 6,5 ].
2. Huit heures
après l’injection du médicament, constatant que le taux d’hématocrite
est à nouveau anormal, on injecte un autre médicament. Le taux
d’hématocrite est alors donné par g (t ) où g est la fonction définie
sur l’intervalle [8 ; 20] par g (t )= −0,003t 2 +0,09t
−0,17, t représentant la durée écoulée depuis l’injection du premier
médicament.
a. Déterminer g ′(t
), où g ′ est la fonction dérivée de la fonction g.
g'(t) = -2 x0,003 t +0,09 = -0,006 t +0,09.
b. Étudier le signe
de g ′(t ) sur [8 ; 20] et dresser le tableau de variation de la
fonction g sur [8 ; 20].
g'(t) = 0 pour t = 0,009 / 0,006 = 15.
g'(t) est négative pour t compris entre ]15 ; 20 ] et positive pour t
compris entre [8 ; 15[.
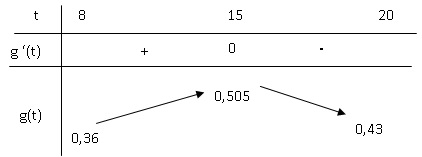
c. Compléter le
tableau des valeurs g (t ) . (on arrondira les valeurs à 10−2
près.)
t
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
g(t)
|
0,36
|
0,40
|
0,43
|
0,46
|
0,48
|
0,49
|
0,50
|
0,51
|
0,50
|
0,49
|
0,48
|
0,46
|
0,43
|
d.
Représenter graphiquement la fonction g.
e. Combien de temps
après la prise de ce second médicament le taux d’hématocrite du patient
est-il redevenu normal ? 1 heure.
Nlle calédonie.
Partie A.
Un laborantin souhaite tester l’efficacité d’un médicament M.
À l’instant t = 0, il injecte à un malade une dose de 2 mL de ce
médicament et il étudie la quantité de médicament présent dans le sang
au bout de t heures. Il s’aperçoit
alors que cette quantité diminue de 12% par heure.
Pour tout entier naturel n, on note un la quantité, en mL,
de médicament présent dans le sang au bout de n heures.
On a alors u0 = 2.
1. Calculer u1
et u2.
u1 = u0 x(1-0,12) = u0 x0,88 =2*0,88 =
1,76 ; u2
= 0,88 xu1 = 0,882 xu0 = 0,882
x2~1,55.
2. Exprimer, pour
tout entier naturel n, un+1 en fonction de un. un+1 = 0,88 un.
3. En déduire la
nature de la suite (un).
On passe d'un terme au suivant en le multipliant par 0,88. Il
s'agit d'une suite géométrique de raison q = 0,88.
4. Exprimer un
en fonction de n. un =
2 x0,88n.
5. Calculer la
quantité demédicament présent dans le sang au bout de 10 heures. On
arrondira le résultat au centième.
u10 = 2 x0,8810 ~0,56.
Partie B.
On note, dans cette partie, f (t ) la quantité de médicament présent
dans le sang au bout de t heures, t appartenant à l’intervalle [0 ;
24]. La courbe C représentative de
la fonction f est donnée.
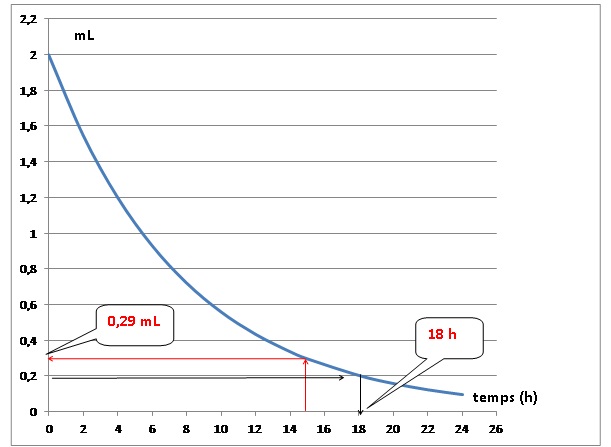
1. Déterminer
graphiquement une valeur approchée de la quantité de médicament présent
dans le sang au bout de 15 heures. 0,29
mL.
2. Résoudre
graphiquement l’inéquation f (t ) < 0,2. Interpréter. [ 18 ; 24 h ].
Au bout de 18 h, la quantité résiduelle de médicament est
inférieure à 0,2 mL.
3. On admet que
pour tout t appartenant à l’intervalle [0 ; 24], f (t ) = 2×(0,88)t
. Vérifier par le calcul les résultats des questions 1. et 2.
f(15) = 2 x0,8815 ~ 0,29 mL.
2×(0,88)t
<0,2 ; 0,88t < 0,2 / 2 ; 0,88t
<0,1 ; t log (0,88) < log (0,1) ;
log (0,1) et log (0,88) sont négatifs ; t > log (0,1) / log (0,88) ;
t > 18.
|
|