Mathématiques, probabilités. Bac St2S 2015.

Mathématiques, probabilités
Bac St2S 2015.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.

.

Métropole.
On parle d’illettrisme pour des personnes adultes qui, après avoir été scolarisées en France, n’ont pas acquis une maîtrise suffisante de la lecture, de l’écriture et du calcul pour être autonomes dans les situations simples de la vie courante.On étudie la population adulte âgée de 18 à 65 ans ayant été scolarisée en France. Selon les données de janvier 2013, on sait que :
• L’effectif total de cette population s’élève à 36 millions d’individus.
• La part de cette population qui a effectué une scolarité complète au collège est de 82%.
• Parmi les personnes ayant effectué une scolarité complète au collège, 97% ne sont pas en situation d’illettrisme.
• Une personne sur quatre, parmi celles qui ont interrompu leur scolarité avant la fin du collège, est en situation d’illettrisme.
Dans la population étudiée, on choisit d’interroger au hasard une personne âgée de 18 à 65 ans qui a été scolarisée en France.
On note C l’évènement : « la personne a effectué une scolarité complète au collège ».
On note I l’évènement : « la personne est en situation d’illettrisme ».
Dans les questions suivantes, les résultats seront arrondis au millième.
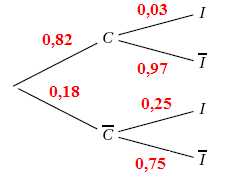
1. Quelle est la probabilité de l’évènement C ? 0,82.
2. Recopier et compléter l’arbre suivant, en reportant sur chaque branche la probabilité correspondante.

3. a. Décrire par une phrase l’évènement C ∩I .
Personnes illettrées ayant effectuées une scolarité complète au collège.
b. Calculer la probabilité de cet évènement.
0,82 x 0,03 = 0,0246.
4. Calculer la probabilité de l’évènement I .
0,82 x 0,03 +0,18 x 0,25 = 0,0246 +0,045 = 0,0696 .
5. Un journaliste affirme dans un article que : « Deux personnes en situation d’illettrisme sur trois ont interrompu leur scolarité avant la fin du collège. » Que penser de cette affirmation? Justifier.
0,18 x 0,25 / 0,0696 = 0,65 ~2 /3. L'affirmation est vraie.

Antilles.
Voici le tableau de la répartition de la population active (en milliers) selon l’âge et le sexe en 2012 en France.

Population active ( milliers) Femmes Hommes Ensemble

15-24 ans 1248 1506 2754

25-49 ans 8672 9461 18133

50-64 ans 3619 3823 7442

65 ans ou plus 100 138 238

Total 13639 14928 28567

Partie A .
1. Quelle était, en 2012, la proportion de femmes de 15-24 ans parmi les femmes actives ?
1248 / 13639 x 100 = 9,15 ~9,2 %.
2. En France, en 2012, les fonctionnaires représentaient 24% de la population active. Quel était, en milliers, le nombre de fonctionnaires cette année là ?
28567 x 0,24 ~ 6856 milliers.
Partie B.
On choisit au hasard et de manière équiprobable une personne dans la population active. On considère les évènements suivants :
A : « La personne est une femme » B : « La personne a entre 25 et 49 ans »
On note P(E) la probabilité d’un évènement E.
1. a. Calculer P(A) et P(B).
p(A) =13639 / 28567 =0,4774.
p(B) = 18133 / 28567 = 0,6348.
b. Décrire à l’aide d’une phrase l’évènement A∪B.
La personne est une femme active ou bien la personne a entre 25 et 49 ans.
c. Vérifier que P(A∪B) ≈ 0,8086.
P(A∪B)=p(A +p(B) -p(A∩B).
p(A∩B) =8672 / 28537 =0,3036.
P(A∪B) =0,4774 +0,6348 -0,3036 ~0,8086.
2. Sachant que la personne choisie est une femme, quelle est la probabilité que cette personne ait entre 25 et 49 ans ?
p_A(B)=p(A∩B) / p(A) =0,3036 / 0,4774 = 0,6359.
3. Les évènements A et B sont-ils indépendants ? Justifier la réponse.
p(A x p(B ) =0,4774 x 0,6348 =0,3030, valeur différente de p(A∩B.
Les événements A et B ne sont pas indépendants.

Polynésie.
.Partie B.
L’Organisation Mondiale de la Santé (OMS) recommande un taux maximum de 15% de césariennes pour ce type de clinique. En France, pour ces mêmes cliniques, les experts estiment que le taux de césariennes est anormal s’il dépasse les 25%.
Un journal régional a mené une enquête auprès d’un certain nombre de femmes ayant accouché dans la clinique en 2014. L’objectif de cette étude était de déterminer si la clinique avait tendance à recourir trop fréquemment à une césarienne sans réelle justification médicale. Lors de cette enquête, le journaliste a obtenu les résultats suivants :
-43% des femmes interrogées sont des primipares (c’est-à-dire qu’il s’agit de leur premier enfant) et parmi elles, 23% ont accouché par césarienne à la clinique.
- 11% des femmes interrogées sont des multipares (c’est-à-dire qu’elles ont déjà accouché auparavant) ayant accouché par césarienne lors d’un accouchement précédent et parmi elles, 64%ont accouché par césarienne à la clinique.
- Les autres sont des multipares n’ayant jamais accouché par césarienne auparavant et parmi elles, 8% ont accouché par césarienne à la clinique.
On choisit au hasard une femme ayant participé à l’enquête. On considère les évènements suivants :
A₀ : « la femme est une primipare » (c’est-à-dire qu’il s’agit de son premier enfant ;
M₁ : « la femme est une multipare qui a déjà accouché par césarienne » ;
M₂ : « la femme est une multipare qui n’a jamais accouché par césarienne auparavant » ;
C : « la femme a accouché par césarienne à la clinique ».
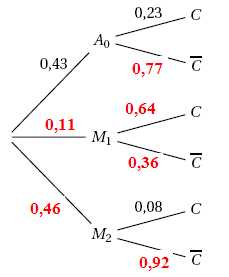
1. À partir des données de l’énoncé, déterminer :
a. La probabilité de l’évènement M₁ notée p (M₁) = 0,11.
b. La probabilité que la femme ait accouché par césarienne sachant qu’elle est une multipare qui a déjà accouché par césarienne, notée P_M1 (C).
P_M1 (C)=0,64.
2. Recopier et compléter l’arbre ci-dessous :

3. Définir par une phrase l’évènement A₀ ∩C puis calculer la probabilité p (A₀ ∩C).
La femme est une primipare qui accouché par césarienne.
p (A₀ ∩C)= 0,43 x 0,23 = 0,0989.
4. Montrer que la probabilité qu’une femme accouche par césarienne dans cette clinique est égale à 0,206 1.
0,43 x 0,23 + 0,11 x 0,64 +0,46 x 0,08 =0,0989 + 0,0704 +0,0368 =0,2061.
5. La clinique étudiée respecte-t-elle les recommandations de l’OMS ? Des experts français ?
Cette valeur est supérieure à 0,15 : la clinique ne respecte pas les recommandations de l'OMS.
Cette valeur est inférieure à 0,25 : la clinique respecte les recommandations de la France.

Antilles septembre.
En 2012, 774 868 permis de conduire en catégorie B ont été délivrés, dont 181 006 via la filière de l’AAC (apprentissage anticipé de la conduite). Le tableau ci-dessous présente les statistiques de réussite à l’examen du permis de conduire de catégorie B pour l’année 2012.

Candidats Ayant suivi l'AAC N'ayant pas suivi l'AAC Total

Reçus 181006 593862 774868

Refusés 65118 484746 549864

Total 246124 1078608 1324732

On choisit au hasard et de manière équiprobable un candidat parmi tous ceux qui ont passé l’examen du permis de conduire de catégorie B en 2012.
On définit les évènements suivants :
A : « le candidat choisi a suivi l’AAC ».
B : « le candidat choisi a été reçu à l’examen ».
Dans cet exercice tous les résultats seront arrondis au centième.
1. a. Quelle est la probabilité que le candidat choisi ait suivi l’AAC?
p(A)= 246124 / 1324732 =0,1858 ~0,19.
b. Quelle est la probabilité que le candidat choisi ait été reçu à l’examen ?
p(B)= 774868 / 1324732 =0,5849 ~0,58.
2. a. Décrire par une phrase l’évènement A∩B.
Le candidat reçu a suivi l'AAC.
b. Donner la probabilité de l’évènement A∩B.
p(A∩B)=181006 / 1324732 =0,1366 ~0,14.
c. Calculer la probabilité de l’évènement A∪B.
p(A∪B) =p(A) +p(B)-p(A∩B)=0,1858 +0,5849 - 0,1366 =0,6341 ~0,63.
3. On note P_A(B) la probabilité que l’évènement B se réalise sachant que l’évènement A est réalisé. Calculer P_A(B).
P_A(B) = p(A∩B) / p(A)=0,1366 / 0,1858 = 0,7352 ~0,74.
4. Dans cette question, toute trace de recherche, même incomplète ou d’initiative même infructueuse, sera prise en compte lors de l’évaluation.
Une personne affirme : « Un candidat qui a suivi l’AAC a plus de chance d’être reçu au permis de conduire qu’un candidat qui ne l’a pas suivi ». Qu’en pensez-vous ?
Proportion de candidats reçus en ayant suivis l'AAC : 181006 / 246124 ~0,74.
Proportion de candidats reçus en n'ayant pas suivis l'AAC : 593862 / 1078608 =0,55.
0,74 >0,55 :l'affirmation est donc vraie.

Métropole septembre.
La Caisse Primaire d’Assurance Maladie (CPAM) réalise une étude sur trois des principales affections de longue durée en répertoriant les patients selon lamaladie qu’ils ont contractée et selon leur sexe. Les affections considérées sont : la leucémie lymphoïde, les anomalies de coagulation et les anomalies du tissu conjonctif. On admet qu’un patient étudié ne peut être atteint que d’une seule maladie. L’étude porte sur 65 955 patients, dont 26 703 hommes.
On observe 28 665 patients atteints d’une leucémie lymphoïde, et parmi ceux-ci, 54% sont des hommes.
Par ailleurs, 55% des patients atteints d’anomalies de coagulation sont des femmes.
1. À l’aide des informations précédentes, compléter les cases grisées de la feuille de calcul donnée. (On arrondira les résultats à l’unité).

A B C D E

1
Patients atteints
de leucémie
lymphoïde Patients atteints
d'anomalies de
coagulation Patients atteints
d'anomalies du
tissu conjonctif Total

2 Homme 28665*0,54=15479 14135*0,55=7774 4863 26703

3 Femme 13186 6361 18292 39252

4 Total 28665 14135 23155 65955

5

6

7

8 Probabilités conditionnelles de chaque pathologie selon le sexe du patient sachant que le patient est un homme

9
Leucémie Anomalies de coagulation Annomalies du
tissu conjonctif

10 Probabilité d'être atteint 0,58 0,24 0,18

2. On choisit au hasard un patient parmi les 65955 ayant participé à l’étude.On considère les évènements suivants :
L : « Le patient est atteint de leucémie lymphoïde ».
C : « Le patient est atteint d’anomalies de coagulation ».
T : « Le patient est atteint d’anomalies du tissu conjonctif ».
H : « Le patient est un homme ».
Dans la suite de cet exercice, les résultats seront arrondis au centième.
a. Calculer la probabilité de l’évènement L, puis celle de l’évènement H.
p(L) =28665 / 65955 =0,4346 ~0,44.
p(H) =26703 / 65655=0,4067 ~0,41.
b. Décrire par une phrase l’évènement 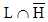, puis calculer sa probabilité.
Le patient est une femme atteint de leucémie lymphoïde ; p(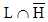) = 13186 / 65955 =0,1999 ~0,20.
c. Calculer la probabilité que le patient soit atteint de leucémie lymphoïde en sachant qu’il s’agit d’un homme.
p(L ∩H)=15479 / 65955=0,2347 ; p_H(L)=p(L ∩H) / p(H) =0,2347 / 0,4067 = 0,5770 ~0,58.
d. Parmi les trois formules suivantes, choisir celle à entrer dans la cellule B10 de la feuille de calcul, de sorte que, recopiée vers la droite jusqu’à la cellule D10, elle permette
d’afficher les probabilités conditionnelles de chaque affection dans le cas où le patient est un homme :
=B2/E2 ; =B2/$E$2 ; =B2/$B$4 .
3. On choisit un patient parmi ceux atteints d’anomalies du tissu conjonctif. Calculer la probabilité que ce patient soit un homme.
p_T(H)=4863 / 23155 =0,21.

menu