Mathématiques,
pourcentages, nuage de points, suite géométrique
Bac St2S 2015.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Métropole.
En l’an 2000, les ventes d’antibiotiques s’élevaient en France à
192 millions de boîtes. La consommation abusive
d’antibiotiques
s’est traduite par un développement des résistances bactériennes. Cette
question préoccupe encore aujourd’hui les autorités sanitaires. En
France, un plan national a été engagé en 2001 sur le thème « les
antibiotiques, c’est pas automatique ».
On a constaté que, de 2000 à
2015, la vente de boîtes d’antibiotiques en France a baissé chaque
année de 2%. On suppose, dans cet exercice, que la baisse de 2% par an
va se poursuivre jusqu’en 2030. On étudie ce modèle.
Le nombre de boîtes d’antibiotiques vendues sera exprimé en millions de
boîtes, arrondi si nécessaire, à 10−3. On
modélise le nombre de boîtes d’antibiotiques vendues en France à l’aide
d’une suite numérique (un). On note u0
le nombre (en millions) de boîtes d’antibiotiques vendues en France en
l’an 2000. Étant donné un entier naturel n, on note un
une estimation, dans le modèle choisi, du nombre (enmillions) de boîtes
d’antibiotiques vendues en France pendant l’année 2000+n. On a donc u0
= 192.
Partie A.
1.
À combien peut-on estimer le nombre de boîtes d’antibiotiques vendues
en 2001 selon le modèle choisi ?
u1 = (1-0,02)u0 = 0,98 u0
= 0,98 x 192 = 188,16.
2. a.
Montrer que la suite (un) est une suite
géométrique et déterminer sa raison.
On passe d'un terme au suivant en multipliant ce terme par 0,98
( raison q =
0,98).
b.
Exprimer un en fonction de n, pour tout entier
naturel n.
un = 0,98n x u0
= 098n x
192.
3.
Estimer, dans le modèle choisi, le nombre de boîtes d’antibiotiques qui
seront vendues en 2017.
n = 7 ; u7 = 192 x0,9817=136,19.
4. a.
Résoudre l’inéquation 192×0,98x <=120.
0,98x >= 120 / 192 ; x log 0,98
>= log (120 / 192) ; -0,00877 x >= -0,204 ; x
>23,27.
b.
En utilisant lemodèle choisi, déterminer à partir de quelle année le
nombre de boîtes d’antibiotiques vendues sera inférieur à 120
millions.
A
partir de l'année 2000 + 24 soit 2024.
Partie B.
Le
tableau ci-dessous, extrait d’une feuille de calcul automatisé, permet
d’observer, tous les 5 ans, l’évolution, en pourcentage, du nombre de
boîtes vendues en France par rapport à celui de l’an 2000. La colonne C
est au format pourcentage et les résultats sont arrondis à 0,01%.
|
A |
B |
C |
| 1 |
Année |
Nombre
de boîtes vendues ( million) |
Evolution
en % |
| 2 |
2000 |
192 |
|
| 3 |
2005 |
173,553 |
-9,61
% |
| 4 |
2010 |
156,878 |
-18,29
% |
| 5 |
2015 |
141,805 |
-26,14
% |
| 6 |
2020 |
128,181 |
-33,24
% |
| 7 |
2025 |
115,865 |
-39,,65
% |
| 8 |
2030 |
104,733 |
-45,45 % |
1. Une formule a
été entrée dans la cellule C3, puis recopiée vers le bas jusqu’à la
cellule C7.
Parmi les trois propositions suivantes, réécrire sur la copie la
formule qui convient :
=(B3 - B2) / B2 ; =(B3 - B2) / 192 ; =(B3
- $B$2) / $B$2.
2.
Calculer la
valeur qui apparaîtra dans la cellule C8.
(104,733-192) / 192 x100 =
-45,45 %.
|
|
|
Antilles.
Le tableau suivant indique le nombre de tués
sur les routes françaises par année :
| Année |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
| Rang
( xi) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Nombre
tués (yi) |
5318 |
4709 |
4620 |
4433 |
4443 |
3992 |
3963 |
3653 |
3268 |
1. a.
Calculer les
coordonnées du point moyen de ce nuage. On arrondira, si nécessaire,
les résultats à l’unité.
xmoyen =(0+1+2+3+4+5+6+7+8)/9 = 4 ;
ymoyen = (5318 + 4709 +4620 +4433 +4443 +392
+3963 +3653 +3268) / 9 = 4267.
b.
Placer dans le repère de l’annexe 1 le point G de coordonnées (4 ; 4
267).
2.
On fait l’hypothèse que l’évolution du nombre de tués sur les routes
françaises est correctement
modélisée par la droite d’ajustement D d’équation y = −220x +5147.
a.
Prouver que le point G appartient à la droite D.
y = -220 x 4 +5147 =4267 ; on retrouve yG.
b.
Tracer la droite D sur le graphique.
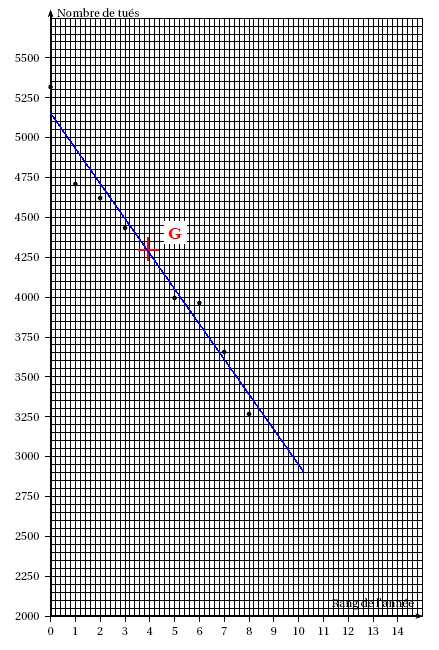
c.
Déterminer, selon ce modèle, une estimation du nombre de tués en 2014.
-220 x 9 +5147 =3167.
3.
On estime que le modèle reste valable jusqu’en 2017.
Selon cet ajustement, à partir de quelle année le nombre de tués
devient-il inférieur à 2 800 ?
-220x +5147 <2800 ; -220x < 2800 -5147 ; 220 x
>=2347 ; x >=10,67 ( 2005+11 = 2016).
|
|
|
|
Polynésie.
Le tableau
suivant, extrait d’une feuille d’un tableur, donne le prix annuel moyen
du paquet de cigarettes (20 cigarettes) le plus vendu, en euros, entre
2000 et 2014.
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
| 1 |
Année |
2000 |
2002 |
2004 |
2006 |
2008 |
2010 |
2012 |
2014 |
| 2 |
Rang
xi |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
| 3 |
Prix
moyen yi |
3,20 |
3,60 |
5 |
5 |
5,30 |
5,65 |
6,30 |
6,70 |
| 4 |
Taux
dévokution ( %)
par rapport à l'année n-2 |
|
|
|
|
|
|
|
|
Partie A .
1. Un journaliste
affirme que le prix entre 2000 et 2014 a augmenté de près de 50%.
L’affirmation est-elle vraie ou fausse ? Justifier.
(6,70-3,20) / 3,20 x 100 ~109 %, l'affirmation est fausse.
2.
La ligne 4 est au format pourcentage. Quelle formule peut-on saisir
dans la cellule C4 et recopier vers la droite pour compléter la ligne 4
?
=(C$3-B$3) /
B$3.
Partie B.
1. a.
Sur la feuille de papiermillimétré fournie, représenter le nuage de
points de coordonnées (xi ; yi
) dans un repère orthogonal .
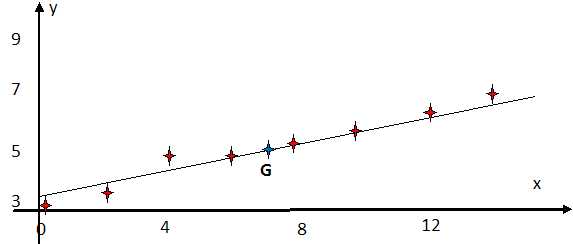
b.
Calculer les coordonnées du point moyen G du nuage de points, puis
placer le point G sur le graphique précédent. Arrondir les résultats à
0,01 près.
xmoyen = (0+2+4+6+8+10+12+14) / 8 = 7.
ymoyen = (3,2 +3,6 +5+5+5,3+5,65+6,3+6,7) / 8 =5,09.
2.
On admet que la droite D d’équation y = 0,24x +3,41 est un bon
ajustement affine du nuage de points et que cet ajustement reste
valable jusqu’en 2025. a.
Vérifier que le point G appartient à la droite D.
0,24 x 7 +3,41 = 5,09; on retrouve l'ordonnée du point G.
b.
Tracer la droite D sur le graphique précédent en indiquant les points
utilisés.
Pour x = 0, y = 3,41 ; pour x = 10 ; y = 5,81.
c.
Selon cet ajustement, quel sera le prix moyen annuel d’un paquet de
cigarettes en France en 2020 ?
x = 20 ; y = 0,24 x 20 +3,41 =8,21
€.
d.
À partir de quelle année celui-ci dépassera-t-il les 10 euros ?
Expliquer la démarche.
0,24x +3,41 >10 ; 0,24 x >10-3,41 ; 0,24 x >6,59 ;
x > 27,45 ( soit 2000 +28 = 2028).
|
|
Antilles
septembre.
Le
tableau
ci-dessous indique les dépenses de santé des soins hospitaliers de
l’année 2008 à l’année 2013.
Année
|
2008
|
2009
|
2010
|
2011
|
2012
|
2013
|
Rang
xi
|
1
|
2
|
3
|
4
|
5
|
6
|
Dépense
( milliards €) yi
|
76
|
79
|
81
|
82
|
84
|
87
|
Partie 1 :
1.
Le montant de la CSBM (consommation de soins et de biens médicaux) pour
l’année 2013 était de 187 milliards d’euros.
Calculer la part des dépenses de santé des soins hospitaliers en 2013
par rapport au montant de la CSBM. On exprimera le résultat en
pourcentage arrondi à 0,1% près.
87 / 187 x100 = 46,5 %
2.
Construire le nuage de points de coordonnées xi
; yi.
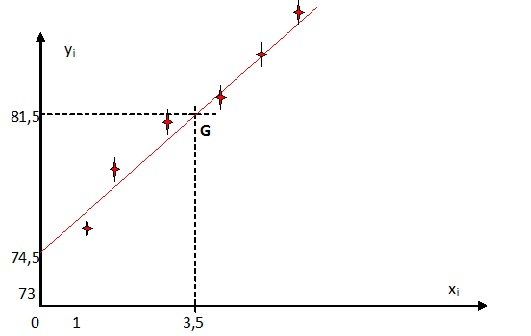
3.
Calculer les coordonnées du point moyen G de ce nuage de points.
xmoyen =(1 +2+3+4+5+6 ) / 6 = 3,5.
ymoyen = (76 +79+81+82+84+87) / 6=81,5.
4. On fait l’hypothèse que l’évolution des dépenses de santé des soins
hospitaliers est correctement modélisée par la droite D d’équation y =
2x +74,5.
a.
Prouver que le point G appartient à cette droite.
2 x3,5 +74,5 = 81,5, on retrouve l'ordonnée du point G.
b.
Tracer la droite D dans le repère précédent.
La droite passe par G et par le point de coordonnées (0 ; 74,5).
c.
Selon ce modèle, estimer la dépense de santé des soins hospitaliers
pour l’année 2014.
x = 7 ; y = 2 x 7 +74,5 = 88,5.
Partie 2 :
Ces mêmes
dépenses de santé des soins hospitaliers ont été saisies dans une
feuille de calcul d’un tableur représentée ci-dessous :
|
A |
B |
C |
D |
E |
F |
G |
| 1 |
Année |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
| 2 |
Dépenses
( milliards €) |
76 |
79 |
81 |
82 |
84 |
87 |
| 3 |
Taux
dévolution |
|
|
|
|
|
|
1. a.
Calculer le taux d’évolution de ces dépenses entre les années 2012 et
2013. On donnera le résultat en pourcentage arrondi à 0, 1% près.
(87-84) / 84 x100=3,57 ~3,6
%.
b.
Donner une formule à saisir dans la cellule C3 pour obtenir, après
recopie vers la droite, les taux d’évolution en pourcentage de ces
dépenses entre deux années consécutives (les cellules de la
ligne 3 sont au format pourcentage).
=(C$2-B$2) /
B$2.
2.
On fait l’hypothèse qu’à partir de l’année 2013, les dépenses de santé
des soins hospitaliers augmentent de 3% tous les ans. Ces dépenses sont
modélisées par la suite géométrique (un) de
premier terme u0 = 87 et de raison 1,03.
a.
Calculer u3. Arrondir le résultat à l’unité.
u3=q3u0
= 1,033 x 87 ~ 95
milliards d'euros.
b.
Que représente u3 dans le contexte de l’exercice
?
u3 représente les dépenses de santé prévues en
2016.
c.
Chaque année le plafond des dépenses de santé des soins hospitaliers
est fixé à 100 milliards d’euros. Selon ce modèle, à partir de quelle
année les dépenses de santé des soins hospitaliers
dépasseront-elles ce plafond ? On justifiera la réponse par un calcul.
un3=qnu0
>=100 ; 1,03n x 87 >= 100 ; 1,03n
>= 100 / 87 ; n log 1,03 > log ( 100 / 87) ; n >
=4,7 ( année 2013 +5 = 2018).
Métropole
septembre.
Partie A.
Depuis 1997, le Conseil européen a adopté une directive concernant
l’évaluation et la gestion de la qualité de l’air ambiant en
agglomération. Pour cela, on calcule lamoyenne annuelle des
concentrations en particules fines en suspension dans l’air, à partir
de mesures effectuées régulièrement. Le tableau ci-dessous indique les
concentrations annuelles moyennes en particules fines dans les grandes
agglomérations belges, exprimées en micro grammes par mètre cube d’air
(μg·m−3).
| Année |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
| Rang
xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Concentration
annuelle yi |
40 |
35 |
34 |
33 |
34 |
33 |
35 |
| Année |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
|
| Rang
xi |
8 |
9 |
10 |
11 |
12 |
13 |
| Concentration
annuelle yi |
31 |
30 |
31 |
26 |
26 |
28 |
Afin d’effectuer des prévisions pour les années futures, les services
sanitaires décident de conduire une étude statistique de ces données.
On a représenté dans un repère orthogonal du plan le nuage de points de
coordonnées (xi ; yi )
associé à ce tableau.
1. Calculer
les coordonnées du point moyen G de ce nuage et le placer dans le
repère.
xmoyen =(1+2+3+4+5+6+7+8+9+10+11+12+13) / 13=7.
ymoyen = (40+35+34+33+34+33+35+31+30+31+26+26+28) / 13 =32.
2. a.
On donne le point A(11 ; 28). Montrer que l’équation réduite de la
droite (AG) s’écrit : y = −x +39. Tracer la droite (AG) sur le
graphique donné.
Equation de la droite y = a x +b.
La droite passe en A : 28 = 11a+b ; la droite passe en G : 32 = 7a+b.
Soustraire : 32-28 = (7-11)a soit a = -1 ; par suite b = 28+11 = 39.
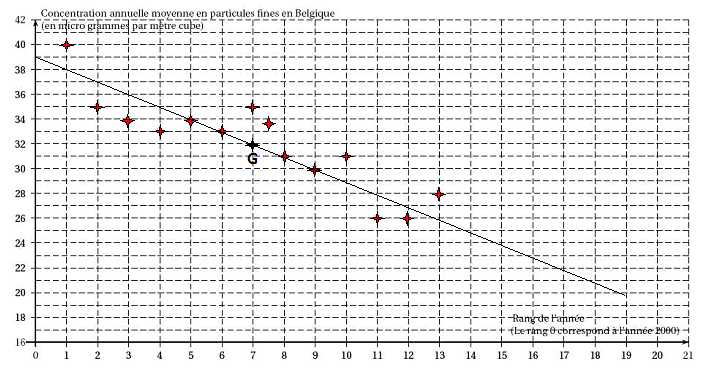
b. En
supposant que la droite (AG) réalise un ajustement affine du nuage
valide jusqu’en 2020, estimer la concentration annuelle moyenne en
particules fines dans l’air des grandes agglomérations
belges pour l’année 2015. y = -15+39 =
24.
Partie B.
Ces particules fines peuvent pénétrer profondément dans les poumons et
y occasionner des inflammations et une détérioration de la santé des
personnes souffrant de maladies pulmonaires ou cardiaques. Par
précaution, le Conseil européen a fixé à 40 microgrammes par mètre cube
la valeur limite maximale de la concentration annuelle moyenne en
particules fines dans l’air.
Afin de respecter cette norme, on a calculé les concentrations
annuelles moyennes dans l’air en particules fines dans les grandes
agglomérations bulgares :
Les services sanitaires bulgares ont mis en place depuis 2013 une série
de mesures incitatives pour réduire la concentration annuelle moyenne
en particules fines. Ils souhaitent ainsi obtenir une diminution de 3%
par an de cette concentration.
Dans cette partie, les résultats seront arrondis au centième.
1.
On modélise à l’aide d’une suite (un) la
diminution souhaitée de 3% par an de la concentration annuelle moyenne
en particules fines dans les grandes agglomérations bulgares.
On pose u0 = 53 et, pour tout entier naturel n
non nul, on désigne par un la concentration
annuelle moyenne souhaitée pour l’année (2013+n).
a.
Calculer les concentrations annuelles moyennes en particules fines
souhaitées pour les années 2014 et 2015.
u1 = (1-0,03)u0 = 0,97 x
53 = 51,41.
u2 = 0,97 x 51,41 = 49,87.
b.
Quelle est la nature de la suite (un) ?
Justifier que la raison est égale à 0,97.
On passe d'un terme au suivant en multipliant ce terme par 1-0,03 =
0,97 : donc suite géométrique de raison q = 0,97 et de premier terme 53.
c.
Exprimer un en fonction de n, pour tout entier
naturel n.
un = qn u0
= 0,97n x53.
d.
Selon cemodèle, calculer la concentration annuelle moyenne en
particules fines souhaitée pour l’année 2019.
n = 0,976 x 53 =44,15.
2. a.
Résoudre l’inéquation 53×0,97x <=40.
0,97x <=40 / 53 ; x log(0,97) <= log(40 / 53) ; -0,01323
x <= -0,1222 ; x > log (40/53) / log (0,97) ; x >9,24.
b.
En déduire à partir de quelle année la Bulgarie pourra atteindre la
valeur limite fixée par le Conseil européen.
2013 +10 = 2023.
|
|