Mathématiques,étude de fonction, suite géométrique. Bac St2S 2015 .

Mathématiques, étude de fonction, suite géomètrique
Bac St2S 2015.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Métropole 2015.
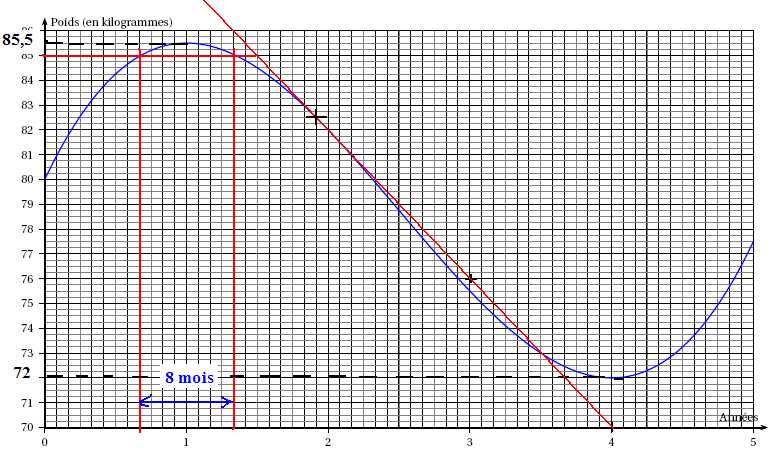
On a tracé sur la feuille annexe la courbe C représentant le poids, en kilogrammes, d’un sportif en fonction du temps, exprimé en années, sur une période d’étude de 5 années.
Partie A : Étude graphique.
Les résultats aux questions posées dans cette partie seront donnés en s’aidant du graphique de l’annexe, avec la précision que permet la lecture graphique et en faisant apparaître les traits de construction utiles. (Un carreau en abscisse correspond à une échelle de temps de 1 mois.)
1. Pendant combien de mois le poids du sportif est-il au-dessus de 85 kilogrammes sur la période étudiée ?
2. Quel est le poids minimum et le poids maximum du sportif sur la période étudiée ?

Partie B : Étude d’une fonction.
On admet que la courbe C est la représentation graphique de la fonction f définie sur l’intervalle [0 ; 5] par
f (x) = x³ −7,5x² +12x +80.
1. La fonction f ′ est la fonction dérivée de la fonction f . Déterminer f ′(x) pour tout réel x appartenant à l’intervalle [0 ; 5].
f '(x) = 3x²-15x+12.
2. Montrer que f ′(x) = (x −1)(3x −12) pour tout réel x appartenant à l’intervalle [0 ; 5].
(x −1)(3x −12) =3x²-12x-3x+12 = 3x²-15x+12.
3. a. Reproduire et compléter le tableau de signes suivant :
b. En déduire le tableau de variations de la fonction f sur l’intervalle [0 ; 5].

c. Cette étude de la fonction f sur l’intervalle [0 ; 5] confirme-t-elle les réponses à la seconde question
de la partie A ? Justifier la réponse.
Oui, augmentation du poids jusqu'à un maxium de 80 kg, puis diminution jusqu' à 72 kg suivie d'une nouvelle augmentation.
4. On veut construire la tangente T à la courbe C au point d’abscisse 2.
a. Déterminer f ′(2) et interpréter graphiquement le résultat.
b. Construire sur le graphique de l’annexe la tangente T en faisant apparaître au moins deux points permettant la construction.
f '(2) =3 x2² -15 x2 +12 = -6.
f '(2) est égale à la pente de la tangente au point d'abscisse 2.
Equation de T : y = -6 x+b ; T passe au point de coordonnées ( 2 ; 82 ).
82 = -6 x 2 +b doù b =94.
T passe au point de coordonnées (3 ; 76) et au point de coordonnées ( 4 ; 70).

Antilles.
On dispose de deux béchers A et B qui contiennent chacun 5 000 bactéries de la même famille. On souhaite
comparer l’efficacité de deux antibiotiques A et B différents sur ces bactéries. On introduit l’antibiotique A dans le bécher A et, au même instant, l’antibiotique B dans le bécher B. On mesure alors, à intervalles réguliers, la quantité (en milliers) de bactéries restantes dans les béchers A et B au fur et à mesure de l’action des antibiotiques.
Partie A : Étude de l’antibiotique A.
Les valeurs mesurées dans le bécher A lors de l’expérience conduisent à modéliser l’évolution du nombre (en milliers) de bactéries dans ce bécher par la fonction f définie sur l’intervalle [0 ; 9] par :
f (t )= 0,05t ² −t +5 où t représente la durée (en heures) écoulée depuis le début de l’expérience.
1. a. Calculer f (0). Ce résultat est-il cohérent avec le nombre de bactéries présentes dans le bécher A au début de l’expérience ?
f(0) = 5 milliers de bactéries initialement, en accord avec les données.
b. Calculer, selon ce modèle, le nombre de bactéries qui seront présentes dans le bécher A au bout de deux heures.
f(2) =0,05 x 2² -2+5 =3,2 milliers.
2. On rappelle que f ′ désigne la fonction dérivée de la fonction f .
a. Déterminer, pour tout nombre réel t de l’intervalle [0 ; 9], une expression de f ′(t ).
f '(t) = 0,1 t-1.
b. Déterminer le signe de f ′(t ) pour tout nombre réel t de l’intervalle [0 ; 9].
f '(t) = 0 pour t = 10 ; f '(t) <0 pour t appartenant à [0 ; 9].
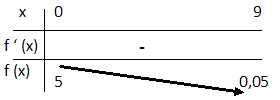
c. Dresser le tableau des variations de la fonction f sur l’intervalle [0 ; 9].

Partie B : Étude de l’antibiotique B
Les valeurs mesurées dans le bécher B lors de l’expérience conduisent à modéliser l’évolution du nombre
(en milliers) de bactéries dans ce bécher par la fonction g définie sur l’intervalle [0 ; 9] par :
g (t )= 5×(0,7)^t où t représente la durée (en heures) écoulée depuis le début de l’expérience.
1. a. Calculer g (0). Que représente cette valeur ?
g(0) = 5 x(0,7)⁰ =5 milliers de bactéries initialement, en accord avec les données.
b. Déterminer le nombre de bactéries présentes dans le bécher B au bout de deux heures.
g(2)=5 x (0,7)² =2,45 milliers.
2. On admet que la fonction g a le même sens de variation que la fonction h(0,7)^t sur l’intervalle
[0 ; 9]. Donner, en justifiant la réponse, le sens de variation de la fonction g sur l’intervalle [0 ; 9].
Si a appartient à l'intervalle ]0 ; 1 [ la fonction a^x est strictement décroissante sur R.
Ici a = 0,7, donc g(x) est strictement décroissante sur [0 ; 9 ].

Partie C : Comparaison de l’efficacité des deux antibiotiques
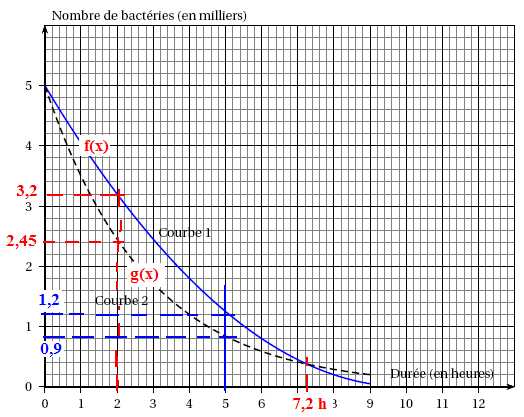
Le graphique suivant présente les courbes représentatives des deux fonctions f et g étudiées précédemment.
1. Indiquer le numéro de la courbe associée à la fonction f et celui de la courbe associée à la fonction g .
2. Déterminer, à l’aide du graphique, à quel(s) instant(s) le nombre de bactéries est identique dans les deux béchers.
A t = 0 et à t = 7,2 h ( 7 h 12 minutes).
3. On estime qu’un antibiotique est efficace sur un humain s’il parvient à diviser par 5 le nombre de bactéries initialement présentes dans le bécher en moins de 5 heures. L’un des deux antibiotiques A ou B est-il efficace pour un humain?
B est efficace ( voir graphe) ; A ne l'est pas.

Par le calcul ; f(5) =0,05 x 5² -5+5 =1,25 milliers, valeur supérieure à 1.
g(5) = 5 x(0,7)⁵=0,84 millier, valeur infpérieure à 1.

Polynésie.
Partie A.
Entre le 1er janvier 2014 et le 31 décembre 2014, une clinique enregistre 1 200 accouchements. Depuis quelques années, le nombre annuel d’accouchements a augmenté en moyenne de 3% par an. L’objectif du directeur de la clinique est d’atteindre les 8 000 accouchements réalisés dans la clinique d’ici fin 2020, en supposant que ce pourcentage d’augmentation moyen reste constant. Pour tout nombre entier naturel n, on note u_n le nombre annuel d’accouchements dans cette clinique pour l’année 2014+n.
Ainsi u₀ est le nombre d’accouchements durant l’année 2014, et u₀ = 1200.
1. Déterminer le nombre d’accouchements qui ont eu lieu dans cette clinique en 2015.
u₁ = (1+0,03) u₀ =1,03 x 1200 =1236.
2. Quelle est la nature de la suite (u_n) ? Justifier et donner ses éléments caractéristiques.
Suite géométrique de raison q = 1,03 et de premier terme 1200: on passe d'un terme au suivant en mltipliant ce terme par 1,03
3. Pour tout entier naturel n, exprimer u_n en fonction de n.
u_n = 1200 x 1,03ⁿ.
4. Déterminer le nombre d’accouchements qui auront lieu dans cette clinique en 2017 selon ce modèle.
u₃ = 1200 x1,03³ ~1311.
5.a. Déterminer le nombre total d’accouchements qui auront eu lieu dans cette clinique entre le 1er janvier 2014 et le 31 décembre 2020.
S = u₀ (1-qⁿ⁺¹) / (1-q) avec n = 6.
S = 1200 (1-1,03⁷) / (1-1,03) = 9195.
b. Selon ce modèle, le directeur de la clinique peut-il espérer atteindre son objectif ? Justifier.
9195 étant supérieur à 8000, l'objectif est atteint.

Bien qu’il soit fortement déconseillé de fumer pendant l’allaitement, certaines femmes continuent de le faire. Il convient alors de respecter de smesures de précaution pour minimiser l’exposition de l’enfant à la nicotine. On s’est intéressé à la concentration de nicotine dans le sang d’une patiente au cours du temps après qu’elle a fumé une cigarette. Elle ne fumera plus pendant toute la durée du test.
On note f (t ) la concentration de nicotine dans le sang de la patiente en nanogramme par millilitre(ng/ml) à l’instant t (en heures). L’instant t = 0 correspond à l’instant où la concentration est maximale (pic sanguin atteint très rapidement).
On admet que f (t )= 25×0,7^t , pour t ∈ [0 ; 10].
1. On admet que sur l’intervalle [0 ; 10] la fonction f a le même sens de variation que la fonction g définie par g (t )= 0,7^t .
Déterminer, en le justifiant, le sens de variation de la fonction f sur l’intervalle [0 ; 10].
Si a appartient à l'intervalle ]0 ; 1 [ la fonction a^x est strictement décroissante sur R.
Ici a = 0,7, donc g(x) est strictement décroissante sur [0 ;10 ].

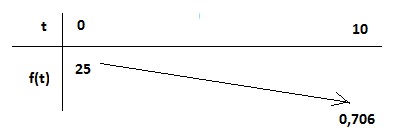
2. Établir le tableau de variation de la fonction f sur l’intervalle [0 ; 10].

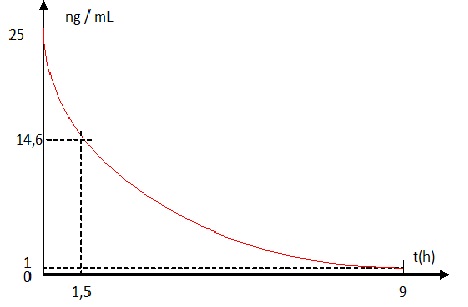
3. La courbe représentative de la fonction f dans un repère orthogonal du plan est donnée.
a. Déterminer graphiquement la concentration de nicotine dans le sang de la patiente au bout d’une heure et demie.
b. Déterminer graphiquement au bout de combien de temps la concentration de nicotine dans le sang a quasiment disparu, c’est-à-dire quand elle devient inférieure ou égale à 1ng/ml.

4. a. Résoudre dans l’intervalle [0 ; 10] l’inéquation : f (t ) <=12,5.
25 x 0,7^t <=12,5 ; 0,7^t <= 12,5 / 25 ; 0,7^t <= 0,5 0,7^t <=0,5.
t log 0,7 <= log 0,5 ; -0,155 t <= -0,301 ; t >1,94 soit t appartenant à [2 ; 10 ].
b. On conseille aux femmes qui fument d’attendre que la moitié de la nicotine présente dans leur sang ait été éliminée avant d’allaiter leur enfant. Combien de temps, à l’heure près, la patiente devra attendre avant de pouvoir allaiter son enfant ? Expliquer la démarche.
Au bout de deux heures le taux de nicotine dans le sang est divisé par deux. Les femmes devront donc attendre 2 heures avant d'allaiter.

Antilles septembre.
Un laboratoire fabrique et commercialise un médicament. Sa capacité de production lui permet de réaliser entre 0 et 7 000 doses de médicament par mois.
On note B la fonction définie sur l’intervalle [0 ; 6] et qui à tout nombre réel x de cet intervalle associe B(x), le bénéfice du laboratoire en milliers d’euros pour une production de x milliers de doses de médicament. La courbe représentative de la fonction B est donnée.
1. Déterminer graphiquement, avec la précision permise par le graphique, le nombre de doses (en milliers) que le laboratoire doit produire par mois pour réaliser un bénéfice supérieur ou égal à 30 milliers d’euros. On donnera le résultat sous la forme d’un intervalle.

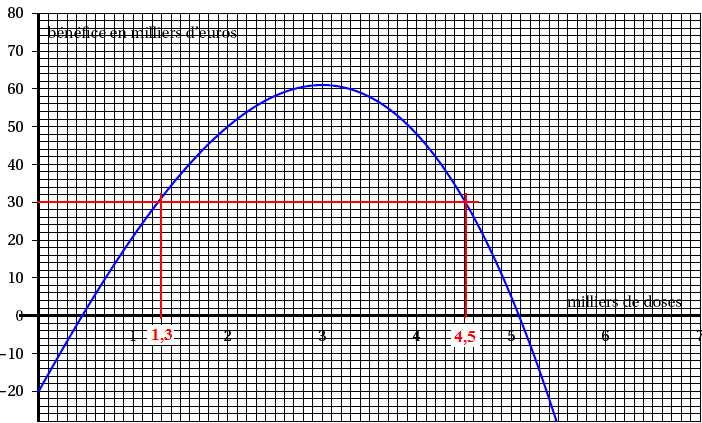
[1,3 ; 4,5 ].
2. On admet que pour tout nombre réel x de l’intervalle [0 ; 6], on a : B(x) = −x³−3x²+45x −20.
On rappelle que B′ désigne la fonction dérivée de la fonction B.
a. Déterminer une expression de B′(x).
B'(x) = -3x²-6x+45.
b. Vérifier que, pour tout nombre réel x de l’intervalle [0 ; 6], on a : B′(x) = (−3x +9)(x +5).
B'(x) = -3x²-15x+9x+45 = -3x²-6x+45
c. Dresser le tableau du signe de B′(x) sur l’intervalle [0 ; 6].
d. En déduire le tableau des variations de la fonction B sur cemême intervalle. On précisera la valeur de B(3).

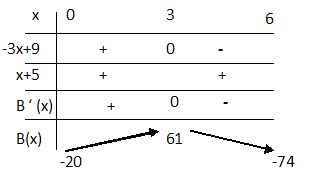
3. Déduire de tout ce qui précède le montant, en euros, du bénéfice maximal.
Bénéfice maximal : 61 000 €.

Métropole septembre.
La grue blanche (grus americana) est un oiseau d’Amérique du Nord. Suite à une chasse intensive et à la détérioration de son habitat, cette espèce est en voie de disparition. En 1938, le nombre de grues blanches sauvages s’élevait à 15 individus. Depuis 1940, les grues blanches font l’objet de plusieurs programmes de protection.
Partie A.
Le nombre de grues blanches sauvages est représenté dans un repère du plan pour les années 1910, 1920, 1928, 1930 et 1938. Une espèce est considérée en « danger critique
d’extinction » si sa population a diminué de plus de 80% sur la période des dix années précédentes.
1. Déterminer graphiquement, avec la précision permise par le graphique et en faisant apparaître les traits de construction nécessaires, le nombre de grues blanches sauvages en 1928.

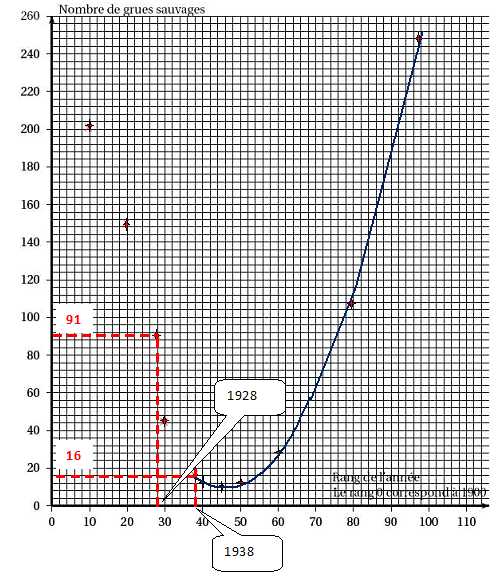
2. Peut-on considérer que les grues blanches sauvages étaient en « danger critique d’extinction » en 1938 ?
Entre 1928 et 1938 le nombre de grues blanches a diminué de 91-16 =75 soit 75 / 91 *100 ~ 82 %. L'espèce est en danger critique d'extinction en 1938..
Partie B.
On suppose que l’évolution de la taille de la population des grues blanches sauvages à partir de 1938 est modélisée par la fonction f définie sur l’intervalle [38 ; 100] par :
f (x) = 0,08x² −7,2x +173
où x est le temps écoulé en années à partir de 1900. Ainsi l’année 1938 correspond à x = 38.
1. a. Compléter le tableau de valeurs donné. Les résultats seront arrondis à l’unité.

x 38 40 45 50 60 80 100

f(x) 15 13 11 13 29 109 253

b. Tracer la courbe représentative de la fonction f.
2. a. La fonction f ′ désigne la fonction dérivée de la fonction f . Déterminer f ′(x) pour tout réel x appartenant à l’intervalle [38 ; 100].
f '(x) = 0,08 *2x -7,2 = 0,16 x-7,2.
b. Déterminer le signe de f ′(x) pour tout x de l’intervalle [38 ; 100].
f '(x)=0 pour x = 7,2 /0,16 =45 ; f '(x) est négative pour x appartenant à [38 ; 45 [ et positive si x appartient à ]45 ; 100].
c. En déduire le tableau des variations de la fonction f sur l’intervalle [38 ; 100].

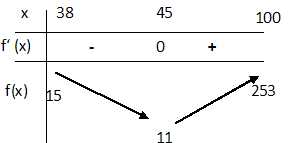
d. Déterminer, selon ce modèle, l’année où le nombre de grues blanches sauvages sera minimal. 1945.

menu