|
|
|
Antilles Guyane 2016.
1. La forme
algébrique du nombre complexe suivant est :
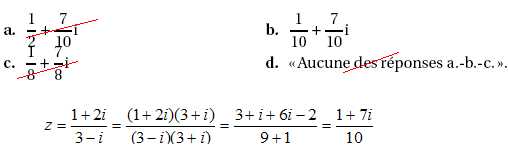
2. La forme
exponentielle du nombre complexe suivant est :
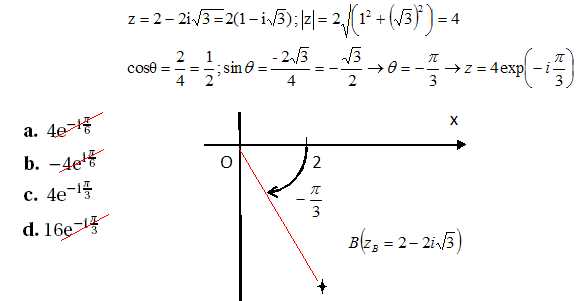
3. Pour tout réel a
strictement positif, lna +ln2a est égal à :
a. ln(3a) ; b. 3lna ; c. ln(2a2), vrai d. 2ln(a2).
lna +ln2a = ln (2a x a) =ln ( 2a2).
4. Une solution f
de l’équation différentielle 3y′′+12y = 0 est la fonction définie pour
tout réel t par :
a. f (t ) = sin(4t
) ; b. f (t )= sin(2t ),
vrai ; c. f (t ) = 2sin(3t ) ; d. « Aucune des réponses a.-b.-c. ».
y′′+4y
= 0 ;
a. ne convient pas : f ' = 4 cos (4t) ; f " = -16 sin (4t).
b. convient. f ' = 2 cos (2t) ; f " = -4 sin (2t) ; -4 sin (2t) + 4 sin
(2t)=0.
c. ne convient pas : f ' = 6 cos (3t) ; f " = -18sin (2t) ;
|
|
Métropole 09 / 2016.
Indiquer si chaque proposition est vraie ou fausse en justifiant.
1.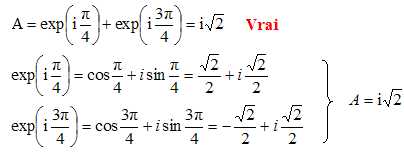
2.
La durée de vie, en heures, d’un composant électronique est une
variable aléatoire T qui suit la loi exponentielle de paramètre l = 5,5×10−4 et
dont la
fonction de densité de probabilité est représentée ci-dessous.
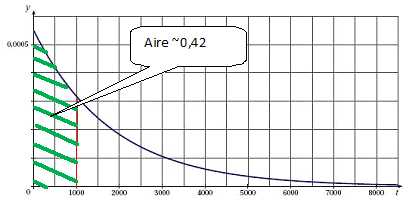
La
probabilité, arrondie à 0,01 près, qu’un composant électronique pris au
hasard ait une durée de vie inférieure à 1 000 heures est 0,35. Faux.
P(T
<= t ) = 1−e−λt ; P(T
<= 1000 ) = 1−exp(
-5,5 10-4 x 1000 ) = 1-exp(-0,55) = 1-
0,577 ~0,42.
3.
La valeur moyenne de la fonction f définie sur l’intervalle [½p : p] par f(x)= cos(x) est −2 /
p. Vrai.
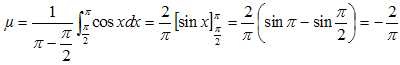
Nlle Calédonie.
1. On considère les
nombre complexe suivants et on calcule leur produit.
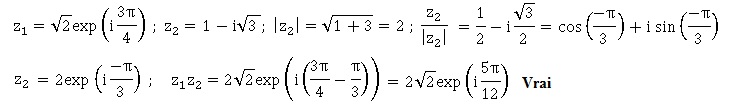
2. La solution f de
l'équation différentielle y" +4y=0 qui vérifie f(0) =-1 et f'(0) = 2
admet comme représentation graphique une sinusoïde d'amplitude 2 et de
période p. Faux.
Equation caractéristique r2 +4= 0 ; solutions r1
=2i et r2 = -2i.
f=Acos (2x+B) avec A et B des constantes.
f(0) = Acos B =-1, f '(0) = -2Asin B = 2 soit A sin ( B) = -1 ; par
suite B = p/4 et
A = 2½.cos(2x+p/4)
f(x) = 2½
Métropole 09 / 2016.
Indiquer si chaque proposition est vraie ou fausse en justifiant.
1.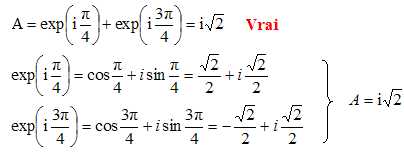
2.
La durée de vie, en heures, d’un composant électronique est une
variable aléatoire T qui suit la loi exponentielle de paramètre l = 5,5×10−4 et
dont la
fonction de densité de probabilité est représentée ci-dessous.

La
probabilité, arrondie à 0,01 près, qu’un composant électronique pris au
hasard ait une durée de vie inférieure à 1 000 heures est 0,35. Faux.
P(T
<= t ) = 1−e−λt ; P(T
<= 1000 ) = 1−exp(
-5,5 10-4 x 1000 ) = 1-exp(-0,55) = 1-
0,577 ~0,42.
3. La valeur moyenne de la fonction
f définie sur l’intervalle [½p
: p] par f(x)=
cos(x) est −2 / p. Vrai.
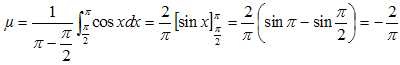
Nlle Calédonie.
1. On
considère les nombre complexe suivants et on calcule leur produit.
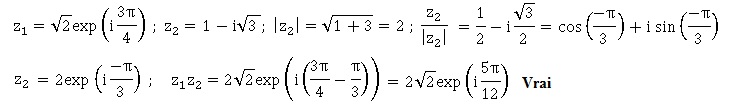
2. La
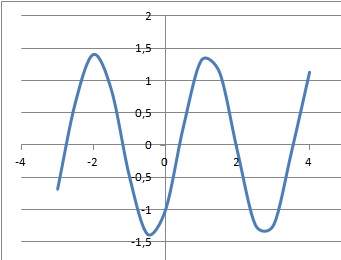
solution f de l'équation
différentielle y" +4y=0 qui vérifie f(0) =-1 et f'(0) = 2 admet comme
représentation graphique une sinusoïde d'amplitude 2 et de période p. Faux.
Equation caractéristique r2 +4= 0 ; solutions r1
=2i et r2 = -2i.
f=Acos (2x+B) avec A et B des constantes.
f(0) = Acos B =-1, f '(0) = -2Asin B = 2 soit A sin ( B) = -1 ; par
suite B = p/4 et
A = - 2½.
f(x) = -2½ cos(2x+p/4).
3. La
solution de l'équation ln(x+3) = 5 est e5-3. Vrai.
x+3 = e5 ; x = e5-3.
4. La durée
de vie en heures d'un certain type d'ampoules électriques est modélisée
par une variable aléatoire qui suit une loi exponentielle de paramètre l = 0,000125 ( exprimé en h-1).
La durée de vie moyenne d'une ampoule est 1250 h. Faux.
1 / 0,000125 = 8000 h.
5. La
fonction F(x) = x ln(x) -x+2 est une primitive de la fonction f(x) =
ln(x) sur l'intervalle ]0 ; +oo[. Vrai.
Dériver F(x) en posant u = x et v = ln(x) ; u' = 1 ; v' = 1/x.
Dérivée de x ln(x) : u'v +v'u = ln(x) +1 ; F '(x) = ln(x) +1-1 =ln(x).
|
|
|