Mathématiques,
Brevet des collèges Amérique du sud 2012
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1. QCM
1. Quelle est
l’expression développée de (3x+5)2 ?
9x2 +25 +30x. Réponse
2. Quelle est
l’expression factorisée de 16x2 −49 ?
(4x)2-72 = (4x-7)(4x+7).
3. Quelle est la
valeur exacte de racine carrée (48) / 2 ?
48 = 16 x3 = 24 x 3.
Racine carrée (48) / 2 = racine carrée (24) x racine carrée
(3) / 2 = 2 x racine carrée (3).
4. La fonction
f(x)=5−4x est affine.
5. L’écriture
scientifique de 65 100 000 est :
6,51 x 10 000 000 = 6,51 107.
Exercice
2.
Pour
gagner le gros lot dans une fête foraine, il faut d’abord tirer une
boule rouge dans une urne, puis obtenir un multiple de trois en
tournant une roue.
1. L’urne contient
6 boules vertes, 5 boules blanches et des boules rouges.
Le responsable annonce « 50% de chances de tirer une boule rouge ».
Combien y a-t-il de boules rouges dans l’urne ?
On note a le nombre de boules rouges.
probabilité de tirer une boule rouge 0,5 = a / (6+5+a).
a = 0,5(11+a) = 5,5 +0,5a ; 0,5 a = 5,5 ; a = 5,5 / 0,5 ; a = 11.
2. On fait
maintenant tourner la roue séparée en 8 secteurs numérotés de 1 à 8.
Quelle est la probabilité d’obtenir un multiple de 3 ?
cas favorables : 3 et 6 , probabilité de tirer un multiple de 3 : 2 / 8
= 1 / 4 = 0,25.
3. Pierre décide de
participer au jeu.
Quelle est la probabilité qu’il gagne le gros lot ?.
0,5 x0,25 = 0,125. ( 1 chance
sur 8 ).
Exercice 3.
1. Les nombres 555 et 240 sont-ils premiers entre eux ?
Justifier.
Non, ils possèdent 1, 5, 3, 15 comme diviseurs communs.
2. Écrire la
fraction 240 /555 sous la forme la plus simple possible. Expliquer la
démarche.
Recherche du PGCD (
240 ; 555 ) à l'aide de l'algorithme d'Euclide :
555 = 2 x240 +75 ; 240 = 3 *75 +15 ; 75 = 5 x15.
240 = 15 x16 ; 555 =15 x 37. 240 / 555 = 16 / 37.
|
|
|
Exercice 4.
Pierre vient d’acheter un terrain dont on peut assimiler la forme à la
figure ci-dessous
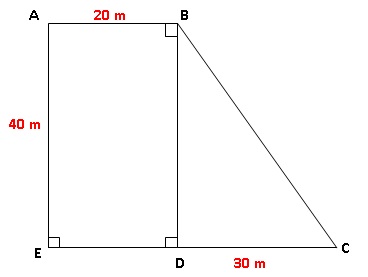
Il souhaite mettre du gazon sur tout le terrain. Pour cela il veut
acheter un produit
qui se présente en sac de 15 kg où il est écrit « 1 kg pour 35 m2
».
1. Combien de sacs
de gazon devrat- il acheter ?
Aire du rectangle : 20 x40 = 800 m2 ; aire du triangle : 40
x30 / 2 = 600 m2.
Aire totale : 800 +600 = 1400 m2.
Nombre de sacs : 1400 / 35 = 40.
2. De plus, il
voudrait grillager le contour de son terrain. Il dispose de 150 m de
grillage, est-ce suffisant ? Justifier.
BC2 = CD2 + BD2 =302 +402
= 900 +1600 = 2500 ; BC = 50 m.
20 +40 +20 +30 +50 = 160 m.
Il ne possède pas suffisamment de grillage.
Exercice
5.
Deux
bateaux sont au large d’une île et souhaitent la rejoindre pour y
passer la nuit. On peut schématiser leurs positions A et B comme
indiquées ci-dessous. Ils constatent qu’ils sont séparés de 800 m, et
chacun voit l’île sous un angle différent. Déterminer, au m près, la
distance qui sépare
chaque bateau de l’île.
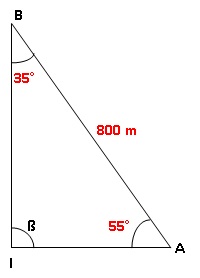
l'angle ß mesure 180 -55-35 = 90°.
sin 35 = AI / AB = AI / 800 ; AI = 800 x sin 35 ~ 459 m.
sin 55 = BI /
AB = BI / 800 ; BI = 800 x sin 55 ~ 655 m.
|
|
|
|
On considère la figure ci-contre où
les droites (EF) et (MN) sont parallèles, les droites (EN) et (FM) sont
sécantes en P.
Déterminer la longueur MN.
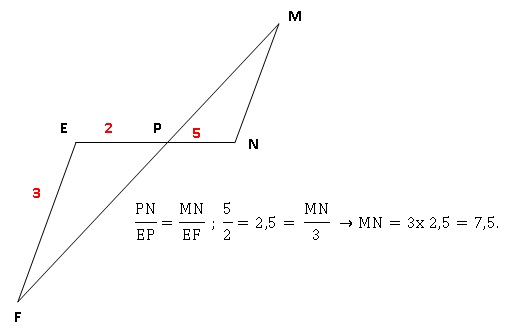
Exercice 6. Lancer
du poids.
Cette discipline sportive consiste à lancer un poids réglementaire, à
partir d’un cercle, le plus loin possible.
I- Le cercle de
lancer.
Pour effectuer son lancer, l’athlète doit prendre son élan dans un
cercle de diamètre 2,14 m.
1. Calculer l’aire
du disque délimité par le cercle de lancer.
pr2
= 3,14 x1,072 ~3,6 m2.
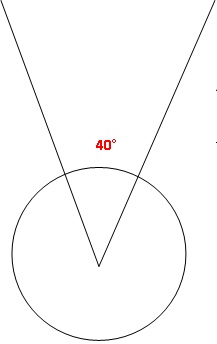
Pour être valable, le jet doit tomber à l’intérieur des deux lignes
inscrites sur le sol et formant un secteur d’un angle de 40 °.
2. Représenter le cercle et la zone de lancer à l’échelle 1 / 50.
2,14 m correspond à 214 / 50 ~4,3 cm.
Le poids est une boule métallique.
Pour être utilisé en compétition, il doit vérifier les conditions
suivantes :
Poids Homme Femme
Homme : diamètre de 110 mm à 130 mm ; masse de 7,26 à 7,285 kg.
Femme : diamètre de 95 mm à 110 mm ; masse de 4 kg à 4,025 kg
Un poids de diamètre 12 cm est composé d’un métal ayant une masse
volumique de 8 g/cm3.
Ce poids vérifie-t-il les conditions nécessaires pour être utilisé en
compétition ?
Volume : V = 4 / 3 p
r3 = 4 /3 x3,14 x63=904,78 cm3.
Masse : 904,78 x 8 ~7238 g = 7,238 kg.
Non , la masse n'est pas comprise entre 7,26 et 7,285 kg.
|
|
Trajectoires
Pour une même impulsion, la longueur du jet du poids varie en fonction
de l’angle de lancer.
Les trois courbes représentent la hauteur (en m) en fonction de
la distance horizontale (en m) parcourue par le poids.
Les courbes (C1), (C2) et (C3)
correspondent à des angles de lancer respectifs de 60 °, 40 ° et 10 °.
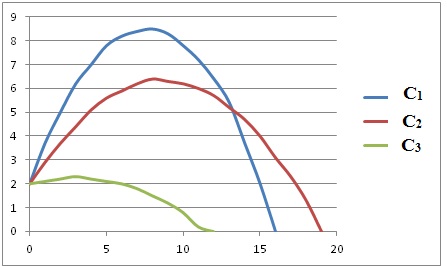
En utilisant ces courbes répondre aux questions suivantes :
1. À quelle hauteur
le poids est-il lâché ? 2 m.
2. Pour quel angle
de lancer, la longueur du jet est-elle la plus grande ? Quelle est
alors la distance obtenue pour ce lancer ?
40° , 19 m.
3. Pour quel angle
de lancer, le poids monte-t-il le plus haut ? Quelle est alors la
hauteur maximum atteinte par le poids ?
60°, 8,5 m.
Performances.
Voici les valeurs (en m) des lancers réalisés par les 11 finalistes
qualifiés aux J. O. de 2008 :
20,06 ; 20,53 ; 21,09 ; 19,67 ; 20,98 ; 20,42 ; 21,51; 21,04 ; 20,41 ;
20,63 ; 21,05.
1. Les médailles
d’or, d’argent et de bronze ont été obtenues respectivement par la
Pologne, les États-Unis et la Biélorussie.
Donner les longueurs de lancer de leurs athlètes.
21,51 m ; 21,09 m ; 21,05 m.
2. Calculer la
longueur de lancer moyenne de cette finale.
(20,06 +20,53 +21,09 +19,67 +20,98 +20,42 +21,51 +21,04 +20,41 +20,63
+21,05) / 11 =20,67 m.
3. L’ukrainien
Yurly Bilonoh a réussi le lancer médian de cette finale. Quelle a été
la longueur de son lancer ?
Ordonner les valeurs : 19,67 ; 20,06 ; 20,41 ; 20,42 ; 20,53 ; 20,63 ; 20,98 ; 21,04 ;
21,05 ; 21,09 ; 21,51.
4. Calculer le
pourcentage des lanceurs qui ont franchi les 21 m.
4 /11 x100 ~36,4 %.
|
|