Mathématiques,
Brevet des collèges Asie 2013
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Le
débit d’une connexion internet varie en fonction de la distance du
modem par rapport au central téléphonique le plus proche. On a
représenté ci-dessous la fonction qui, à la distance du modem au
central téléphonique (en kilomètres), associe son débit théorique (en
mégabits par seconde).
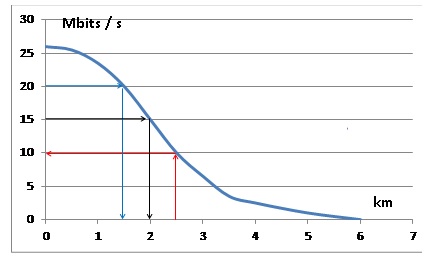
1. Marie habite à
2,5 km d’un central téléphonique. Quel débit de connexion obtient-elle
?
10 Mbits /s
2. Paul obtient un débit de 20
Mbits/s. À quelle distance du central téléphonique habite-t-il ? 1,5 km.
3. Pour pouvoir
recevoir la télévision par internet, le débit doit être au moins de 15
Mbits/s.
À quelle distance maximum du central doit-on habiter pour pouvoir
recevoir la télévision par internet ? Moins de 2 km.
Exercice 2.
Pour chacune des quatre affirmations suivantes,
préciser si elle est vraie ou fausse et justifier la réponse.
1. Le PGCD de 18 et
de 36 est 9. Faux.
36= 18 +18 ; 18 = 18+0. Le PGCD de 18 et 36 est égal à 18.
2. Le double de 9
/ 4 est égal à 9 /2. Vrai.
9 / 4 x2 = (9 x2) / 4 = 9 / 2.
3. Le carré de 3x
racine carrée (5) est égal à 15. Faux.
32 x5 = 45.
4. Pour tous les
nombres x, on a (2x +3)2= 9+2x(2x +3). Faux.
(2x +3)2=4x2+12x+9
=2x(2x +6) +9.
|
|
|
Exercice 3.
Le
jeu de fléchettes consiste à lancer 3 fléchettes sur une cible. La
position des fléchettes sur la cible détermine le nombre de points
obtenus.
La cible est installée de sorte que son centre se trouve à 1,73 m du
sol. Les pieds du joueur ne doit pas s’approcher à moins de 2,37 m
lorsqu’il lance les fléchettes. Pour cela, un dispositif électronique
est installé qui en mesurant l’angle calcule automatiquement la
distance du joueur au mur. Il sonne si la distance n’est pas
réglementaire.
1.
Un joueur s’apprête à lancer une fléchette. La droite passant par le
centre de la cible et son pied fait un angle de 36,1° avec le sol. Le
mur est perpendiculaire au sol.
Est-ce que la sonnerie va se déclencher ? Justifier la réponse.
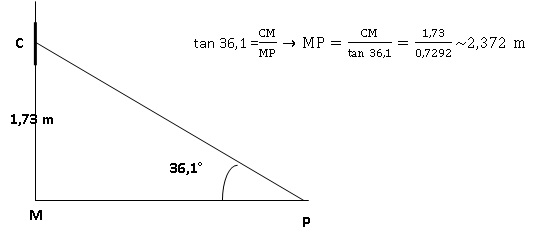
MP > 2,37 m, la sonnerie ne se déclenche pas.
2. On a relevé
dans
le tableau ci-dessous les points obtenus par Rémi et Nadia lors de sept
parties de fléchettes. Le résultat de Nadia lors la partie 6 a été
égaré.
Partie
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Moyenne
|
Médiane
|
Rémi
|
40
|
35
|
85
|
67
|
28
|
74
|
28
|
51
|
40
|
Nadia
|
12
|
62
|
7
|
100
|
81
|
65
|
30
|
51
|
62
|
a. Calculer le nombre moyen de
points obtenus par Rémi.
(40 + 35 +85 +67 +28 +74 +28 ) / 7 =51
b. Sachant que
Nadia a obtenu en moyenne 51 points par partie, calculer le nombre de
points qu’elle a obtenus à la 6e partie.
( 12 +62 +7 +100 +81 +30 +x) / 7 = 51 ;
292 +x =51 x7 = 357 ; x =357-292= 65.
c. Déterminer la
médiane de la série de points obtenus par Rémi, puis par Nadia.
Rémi : 28 ; 28 ; 35 ; 40
; 67 ; 74 ; 85.
Nadia : 7 ; 12 ; 30 ; 62
; 65 ; 81 ; 100.
Exercice 4.
On considère le programme de calcul suivant :
• Choisir un nombre
• Ajouter 5
• Prendre le carré de cette somme
1. Quel résultat
obtient-on lorsqu’on choisit le nombre 3 ? le nombre −7 ?
(3+5)2=64 ; (-7+5)2=(-2)2 = 4.
2. a. Quel nombre
peut-on choisir pour obtenir 25 ?
(x+5)2=25 ; x+5 = ±5.
x =0 et x = -10.
b. Peut-on obtenir
−25 ? Justifier la réponse.
Non, un carré est positif ou nul.
3. On appelle f la
fonction qui, au nombre choisi, associe le résultat du programme de
calcul.
a. Parmi les
fonctions suivantes, quelle est la fonction f ?
x2 ; faux ; x2+5 ; faux ; (x+5)2,
vrai ; 2(x+5), faux.
b. Est-il vrai que
−2 est un antécédent de 9 ? Vrai.
(x+5)2 = 9 ; x+5 =
±3 ; x = -2 et x = -8.
4. a. Résoudre l’équation (x +5)2=
25.
(x+5)2=25 ; x+5 = ±5.
x =0 et x = -10
|
|
|
|
Exercice 5.
1. Une ville de 50 000 habitants
dépense 10 euros par mois et par habitant pour faire traiter les
poubelles ménagères.
Quel est le budget sur une année de cette ville pour faire traiter les
poubelles ? Justifier la réponse.
10 x12 x50000=6 000 000 €.
2. En 2009, la
France comptait 65 millions d’habitants qui ont produit 30 millions de
tonnes de déchets.
Est-il vrai que cette année là, un habitant en France produisait un peu
plus de 1 kg de déchet par jour ? Justifier la réponse.
30 / 65=0,4615 tonne par habitant par an.
461,5 kg par
habitant par an.
461,5 / 365=1,26 kg par habitant par jour. Affirmation vraie.
Exercice 6.
Voici un article trouvé sur internet.
D’après l’Observatoire des Usages Internet de Médiamétrie, au dernier
trimestre 2011, 28 millions d’internautes ont acheté en ligne. Au
premier trimestre de 2012, on constate une augmentation de 11% du
nombre d’achats en ligne.
1. En utilisant les
données de cet article, calculer le nombre de cyberacheteurs au premier
trimestre 2012. Arrondir le résultat à 0,1 million près.
28 x1,11 =31,08 ~31,1 millions.
2. Si la
progression sur le deuxième trimestre 2012 est, elle aussi, de 11%,
quelle serait la progression en pourcentage sur les deux trimestres ?
Justifier la réponse.
28 x1,11 x1,11= 28 x1,2321 soit une progression d'environ +23,2 %.
|
|
Exercice 7.
Un
moule à muffins est constitué de 9 cavités. Toutes les cavités sont
identiques. Chaque cavité a la forme d’un tronc de cône (cône coupé par
un plan parallèle à sa base).
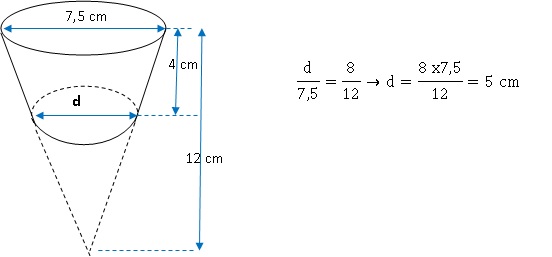
1. Montrer que le
volume d’une cavité est d’environ 125 cm3.
Volume du grand cône : 1 /3 *3,14 x(7,5 / 2)2 x12 = 176,7 cm3.
Volume du petit cône : 1 /3 *3,14 x(5 / 2)2
x8 = 52,36 cm3.
Volume de la cavité : 176,7 -52,36 =124,34 ~125 cm3.
2. Léa
a préparé 1 litre de pâte. Elle veut remplir chaque cavité du moule au
3 /4 de son volume.
A-t-elle suffisamment de pâte pour les 9 cavités du moule ? Justifier
la réponse.
Volume de pâte par cavité : 125 x3 /4=93,75 cm3.
Volume de pâte pour 9 cavités : 9 x93,72 = 843,75 cm3 =
0,843 L.
Elle a suffisamment de pâte.
Exercice 8.
La
ville BONVIVRE possède une plaine de jeux bordée d’une piste cyclable.
La piste cyclable a la forme d’un rectangle ABCD dont on a « enlevé
trois des coins ».
Le chemin de G à H est un arc de cercle ; les chemins de E à F et de I
à J sont des segments.
Les droites (EF) et (AC) sont parallèles.
Quelle est la longueur de la piste cyclable ? Justifier la réponse.
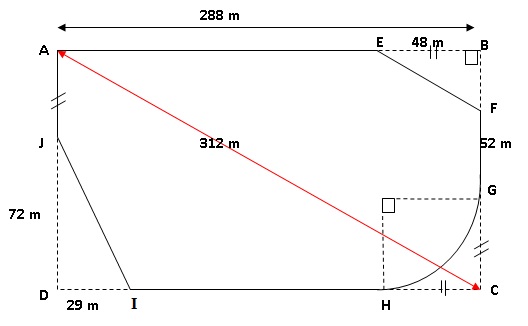
AD2 = AC2 -AB2 =3122-2882=
14400 ; AD = 120 m.
AE = 288-48 =240 m.
BF = 120-52-48 =20 m.
EF2 = BE2 +BF2 =482+202=
2704 ; EF = 52 m.
Longueur de l'arc de cercle GH : 3,14 x48 /2~75,4 m.
HI = 288 -29 -48 = 211 m.
IJ2 = DI2 +DJ2 =292+722=
6025 ; IJ ~ 77,6 m.
Longueur de la piste : 240 +52 +52 +75,4 +211 +77,6 +48 = 756 m.
.
|
|