Mathématiques, Brevet des collèges Métropole 2013

Mathématiques, Brevet des collèges Métropole 2013

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1.
Avec un logiciel :
- on a construit un carré ABCD, de côté 4 cm.
- on a placé un point M mobile sur [AB] et construit le carré MNPQ
- on a représenté l’aire du carré MNPQ en fonction de la longueur AM.
En utilisant ce graphique répondre aux questions suivantes. Aucune justification n’est attendue.

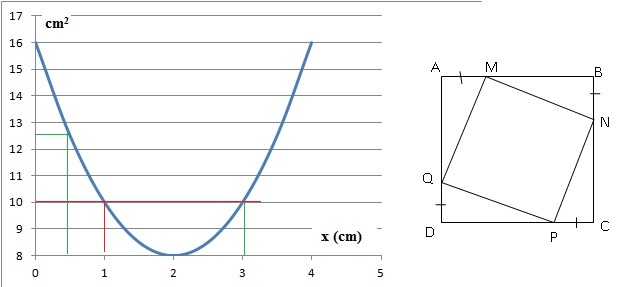
1. Déterminer pour quelle(s) valeur(s) de AM, l’aire de MNPQ est égale à 10 cm² .
1 et 3 cm.
2. Déterminer l’aire de MNPQ lorsque AM est égale à 0,5 cm.
12,5 cm².
3. Pour quelle valeur de AM l’aire de MNPQ est-elle minimale ? Quelle est alors cette aire ?
AM = 2 cm ; l'aire minimale vat 8 cm².

.
.

Exercice 2.
On a utilisé un tableur pour calculer les images de différentes valeurs de x par une fonction affine f et par une autre fonction g .Une copie de l’écran obtenu est donnée ci-dessous.

C2
f(x)
=-5*C1+7

A
B
C
D
E
F
G
H

1
x
-3
-2
-1
0
1
2
3

2
f(x)
22
17
12
7
2
-3
-8

3
g(x)
13
8
5
4
5
8
13

4

1. Quelle est l’image de −3 par f ? 22.
2. Calculer f (7).
f(7) = -5 x7 +7 = -28.
3. Donner l’expression de f (x).
f(x) = -5x+7.
4. On sait que g (x) = x²+4. Une formule a été saisie dans la cellule B3 et recopiée ensuite vers la droite pour compléter la plage de cellules C3 :H3. Quelle est cette formule ?
=B1*B1+4

Exercice 3.
Les informations suivantes concernent les salaires des hommes et des femmes d’une même entreprise :
Salaires des femmes :
1 200 €; 1 230 €; 1 250 €; 1 310 € : 1 376 €; 1 400 €; 1 440 €; 1 500 €; 1 700 €; 2 100 €
Salaires des hommes :
Effectif total : 20
Moyenne : 1 769 €
Étendue : 2 400 €
Médiane : 2 000 €
Les salaires des hommes sont tous différents.
1. Comparer le salaire moyen des hommes et celui des femmes.
Salaire moyen des femmes ;( 1200 +1230 +1250 +1310 +1376 +1400 +1440 +1500 +1700 +2100 ) / 10 =1450,6 €
2. On tire au sort une personne dans l’entreprise. Quelle est la probabilité que ce soit une femme ?
10 femmes sur 30 employés : 10 / 30 = 1 /3.
3. Le plus bas salaire de l’entreprise est de 1 000 €.Quel salaire est le plus élevé ?
1000 +2400 = 3400 €.
4. Dans cette entreprise combien de personnes gagnent plus de 2 000 € ?
La moitié des hommes + une femme soit 11 personnes.

Exercice 4.
Trois figures codées sont données ci-dessous. Elles ne sont pas dessinées en vraie grandeur. Pour chacune d’elles, déterminer la mesure de l’angle� ABC.

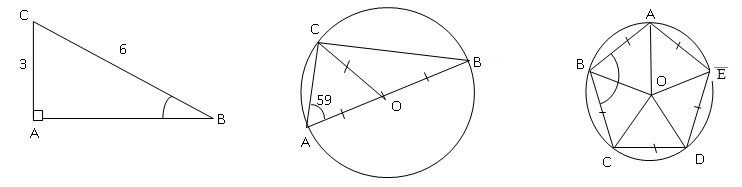
Triangle rectangle de gauche : sin (ABC) = AC / BC = 3 / 6 = 0,5 ; ABC = 30°.
Triangle rectangle inscrit dans un demi-crcle de centre O, de rayon OB : ABC = 90-59 = 31°.
Pentagone régulier inscrit dans un cercle :
l'angle au centre AOC, obtu, mesure 360 / 5 x3=3 x 72 °= 216°.
L'angle inscrit ABC intercepte le même arc que l'angle au centre AOC. ABC mesure 216 / 2 = 108 °.

.
.

Exercice 5. Pour réaliser un abri de jardin en parpaing, un bricoleur a besoin de 300 parpaings de dimensions 50 cm× 20 cm× 10 cm pesant chacun 10 kg. Il achète les parpaings dans un magasin situé à 10 km de sa maison. Pour les transporter,il loue au magasin un fourgon.
Information 1 : Caractéristiques du fourgon :
- 3 places assises.
- Dimensions du volume transportable (L ×l ×h) : 2,60 m× 1,56 m× 1,84 m.
- Charge pouvant être transportée : 1,7 tonne.
- Volume réservoir : 80 litres.
-Diesel (consommation : 8 litres aux 100 km).
Information 2 : Tarifs de location du fourgon par jour
30 km maxi : 48 € ; 50 km maxi : 55 € ;100 km maxi : 61 € ; 200 km maxi : 78 € ; km supplémentaire 2 €.
Ces prix comprennent le kilométrage indiqué hors carburant
Un litre de carburant coûte 1,50 €.
1. Expliquer pourquoi il devra effectuer deux aller-retour pour transporter les 300 parpaings jusqu’à sa maison.
Masse totale des parpaings : 300 x10 = 3000 kg = 3 t.
La charge maximale transportée est 1,7 t.
Il peut mettre 5 parpaings dans la longueur et 15 dans la largeur soit 75 par rangée ; il peut réaliser 9 rangées ; le volume du fourgon permettrait de ranger 75 x9 = 675 parpaings. Ce n'est pas le volume qui limite, mais bien la charge maximale transportée.
2. Quel sera le coût total du transport ?
Distance parcourue : 2 x(10+10)= 40 km ; coût de la location : 55 €.
Consommation : 8 x40 / 100 = 3,2 L ; coût 3,2 x1,5 = 4,8 €.
Total : 59,8 €.
3. Les tarifs de location du fourgon sont-ils proportionnels à la distance maximale autorisée par jour ?
Non : 48 / 30 diffère de 55 / 50 diffère de 61 / 100....

Exercice 6.
Dans les marais salants, le sel récolté est stocké sur une surface plane. On admet qu’un tas de sel a toujours la forme d’un cône de révolution.
1. a. Pascal souhaite déterminer la hauteur d’un cône de sel de diamètre 5 mètres. Il possède un bâton de longueur 1 mètre. Il effectue des mesures et réalise les deux schémas ci-dessous :
Démontrer que la hauteur de ce cône de sel est égale à 2,50 mètres.

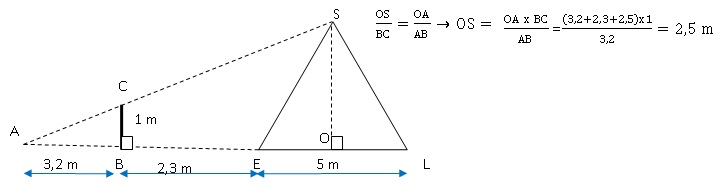
b. À l’aide de la formule V_cône=aire de base x hauteur / 3 , déterminer en m³ le volume de sel contenu dans ce cône. Arrondir le résultat au m³ près.
V_cône = 3,14 x2,5² x 2,5 / 3 = 16,36 ~16 m³.
2. Le sel est ensuite stocké dans un entrepôt sous la forme de cônes de volume 1 000 m³. Par mesure de sécurité, la hauteur d’un tel cône de sel ne doit pas dépasser 6 mètres. Quel rayon faut-il prévoir au minimum pour la base ? Arrondir le résultat au décimètre près.
Aire de base = V_cône x3 / hauteur = 3000 / 6 = 500 m².
500 = 3,14 R² ; R = racine carrée ( 500 / 3,14) = 12,6 m.

Exercice 7.
Chacune des trois affirmations suivantes est-elle vraie ou fausse ? On rappelle que
les réponses doivent être justifiées.
Affirmation 1 : Dans un club sportif les trois quarts des adhérents sont mineurs et le tiers des adhérents majeurs a plus de 25 ans. Un adhérent sur six a donc entre 18 ans et 25 ans.
On note x le nombre d'adhérents : 0,75 x sont mineurs et 0,25 x sont majeurs.
0,25 x / 3 ont plus de 25 ans et 2 x0,25 / 3 x = x / 6 ont entre 18 et 25 ans. l'affirmation est vraie.
Affirmation 2 : Durant les soldes si on baisse le prix d’un article de 30% puis de 20%, au final le prix de l’article a baissé de 50%. Faux.
Pour un article de 1 €, prix après la première baisse : 0,7 € ; prix après la seconde baisse : 0,7 x (1-0,2) =0,56 ( 56 %).
Affirmation 3 : Pour n’importe quel nombre entier n, (n +1)²−(n −1)² est un multiple de 4. Vrai.
Différence de deux carrés : (n+1 +n-1)(n+1-n+1) = 2 n x 2 = 4 n.

.

menu