Mathématiques,
Brevet des collèges Pondichéry 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Cet exercice est un QCM(questionnaire à choix multiples). Pour chaque
ligne du tableau, une seule affirmation est juste.
Sur votre copie, indiquer le numéro de la question et recopier
l’affirmation juste. On ne demande pas de justifier.
|
Questions
|
A
|
B
|
C
|
1
|
La
forme développée de (x-1)2 est
|
(x-1)(x+1)
faux
|
x2-2x+1 Vrai
|
x2+2x+1
Faux.
|
2
|
Une
solution de l'équation 2x2 +3x-2=0 est
|
0
Faux
|
2
Faux
|
-2 Vrai
|
3
|
On
cosidère la fonction f(x) = 3x +2. Un antécédent de -7 par la fonction
f est
|
-19
Faux
|
-3 Vrai
|
-7
Faux
|
4
|
Lorsqu'on
regarde un angle de 18° à la loupe de grossissement 2, on voit un angle
de :
|
9°
Faux
|
36°
Faux
|
18° Vrai.
|
5
|
On
considère la fonction g(x) = x2+7. Quelle est la formule à
entrer dans la cellule B2 pour calculer g(-2) ?
|
=A2^2+7
Vrai
|
=
-22+7
|
=A2
x2 +7
|
Exercice 2.
Un chocolatier vient de fabriquer 2 622 oeufs de Pâques et 2 530
poissons en chocolat.
Il souhaite vendre des assortiments d’oeufs et de poissons de façon que
:
• tous les paquets aient la même composition ;
• après mise en paquet, il reste ni oeufs, ni poissons.
1. Le chocolatier
peut-il faire 19 paquets ? Justifier.
2622 / 19 = 138 ; 2530 / 19 = 133 +3.
Non, il reste 3 poissons.
2. Quel est le plus
grand nombre de paquets qu’il peut réaliser ?
Dans ce cas, quelle sera la composition de chaque paquet ?
2622 = 2 x 3 x 19 x 23 ; 2530 = 2 x 5 x11 x23.
Le PGCD de 2622 et de 2530 est égal à 2x 23 = 46.
Il peut réaliser 46 paquets contenant chacun 2622 / 46 = 57 oeufs et
2530 / 46 = 55 poissons.
|
...
|
|
|
Exercice 3.
Peio, un jeune Basque décide de vendre des glaces du
1er juin au 31 août inclus à Hendaye.
Pour vendre ses glaces, Peio hésite entre deux emplacements :
une paillotte sur la plage ou une boutique au centre-ville.
En utilisant les informations ci-dessous, aidez Peio à choisir
l’emplacement le plus rentable.
Information 1
: les loyers des deux emplacements proposés :
• la paillotte sur la plage : 2 500 € par mois.
• la boutique au centre-ville : 60 € par jour.
Information 2
: lamétéo à Hendaye
Du 1er juin au 31 août inclus :
• Le soleil brille 75% du temps
• Le reste du temps, le temps est nuageux ou pluvieux.
Information 3
: prévisions des ventes par jour selon la météo :
|
Soleil
|
Nuageux
pluvieux
|
La
paillote
|
500
€
|
50
€
|
La
boutique
|
350
€
|
300
€
|
Nombre total de journées ensolléillées :
(30+31+31) x0,75 = 69 jours ; donc 23 journées pluvieuses.
Recette paillote : 500 x 69 +50 x23 = 35 650 €.
Net = 35 650 -2500 x 3 = 28 150 €.
Recette boutique : 350 x69 +300 x 23 = 31 050 €.
Net = 31050 -60 x92 = 25 530 €.
Peio gagnera un peu plus sur la plage.
Exercice 4.
La
dernière bouteille de parfum de chez Chenal a la forme d’une pyramide
SABC à base triangulaire de hauteur [AS] telle que ABC est un
triangle rectangle et isocèle en A ; AB = 7,5 cm et AS = 15 cm.
1. Calculer le
volume de la pyramide SABC. (On arrondira au cm3 près.)
Aire de la base : A = AB x AC / 2 = 7,5 x7,5 / 2 = 28,125 cm2
; hauteur AS = 15 cm.
Volume V = A x AS / 3 = 28,125 x15 / 3 = 140,625 ~141 cm3.
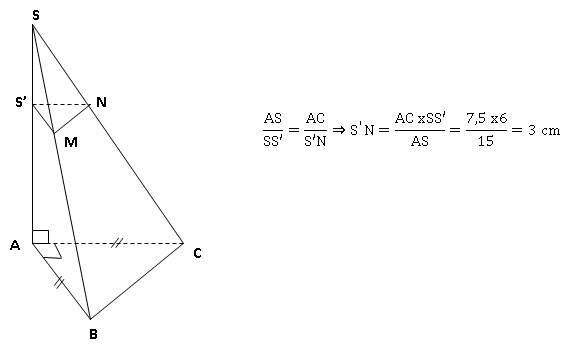
2. Pour fabriquer
son bouchon SS′MN, les concepteurs ont coupé cette pyramide par un plan
P parallèle à sa base et passant par le point S′ tel que SS′ = 6 cm.
a. Quelle est la
nature de la section plane S′MN obtenue ?
Triangle rectangle isocèle en S'.
b. Calculer la
longueur S′N.
3. Calculer le
volume maximal de parfum que peut contenir cette bouteille en cm3.
Volume de la petite pyramide : aire de base x hauteur / 3 = 3 x3
/ 2 x6 / 3 =9 cm3.
141-9 = 132 cm3.
|
|
|
|
Exercice 5.
Un jeu télévisé propose à des candidats deux épreuves :
• Pour la première épreuve, le candidat est face à 5 portes : une seule
porte donne accès à la salle du trésor alors que les 4 autres s’ouvrent
sur la salle de consolation.
• Pour la deuxième épreuve, le candidat se retrouve dans une salle face
à 8 enveloppes.
Dans la salle du trésor : 1 enveloppe contient 1 000 €, 5 enveloppes
contiennent 200 €. Les autres contiennent 100 €.
Dans la salle de consolation : 5 enveloppes contiennent 100 € et les
autres sont vides.
Il doit choisir une seule enveloppe et découvre alors le montant qu’il
a gagné.
1. Quelle est la
probabilité que le candidat accède à la salle du trésor ?
Une seule porte sur 5, la probabilité d'accéder au trésor est donc 1 /
5 = 0,2.
2. Un candidat se
retrouve dans la salle du trésor.
a. Représenter par
un schéma la situation.
Probabilité que le candidat ouvre l'enveloppe contenant 1000 € :
p(M) = 1 /8 = 0,125.
Probabilité que le candidat ouvre une enveloppe contenant 200 € :
p(D) = 5 /8 = 0,625.
Probabilité que le candidat ouvre une enveloppe contenant 100 € :
p(C) = 2 /8 = 0,25.
b. Quelle est la probabilité qu’il gagne aumoins 200 € ?
P(M) +p(D) = 0,125 +0,625 = 0,75.
3. Un autre
candidat se retrouve dans la salle de consolation.
Quelle est la probabilité qu’il ne gagne rien ?
Trois enveloppes sur huit sont vides. P(R) = 3 / 8 =0,375.
Exercice 6.
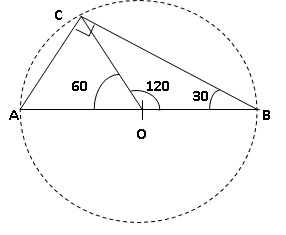
[AB] est un segment de milieu O tel que AB = 12 cm.
Le point C appartient au cercle de centre O passant par A. De plus AC =
6 cm
L’angle� ABC mesure 30 °.
1. Construire la
figure en vraie grandeur.
2. Les affirmations
suivantes sont-elles vraies ou fausses ? Justifier.
a. Le triangle ABC
est rectangle. Vrai.
Un triangle inscrit dans un demi-cercle est rectangle.
b. Le segment [BC]
mesure 10 cm. Faux.
cos 30 = BC / AB ; BC = AB cos 30 = 12 x 0,866 ~10,4 cm.
c. L’angle� AOC
mesure 60 °. Vrai.
L'angle inscrit ABC mesure 30 ° et intercepte l'arc AC.
L'angle au centre AOC intercepte l'arc AC.
d. L’aire du
triangle ABC est 18 x racine carrée (3) cm2. Vrai.
AC x BC / 2 = AC x AB cos 30 / 2=6 x 12 x cos 30 / 2.
e. L’angle �BOC
mesure 31 °. Faux.
Cet angle est obtu, sa mesure est supérieure à 90 °.
|
|
Exercice 7.
Trois
triangles équilatéraux identiques sont découpés dans les coins d’un
triangle équilatéral de côté 6 cm. La somme des périmètres des trois
petits triangles est égale au périmètre de l’hexagone gris restant.
Quelle est la mesure du côté des petits triangles ?
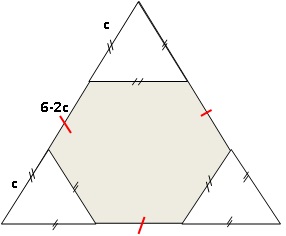
Périmètre d'un petit triangle : 3 c.
Périmètre des trois petits triangles : 9 c.
Périmètre de l'hexagone gris : 3 c + 3(6-2c) = 18-3c.
9c = 18-3c ; 12 c = 18 ; c = 18 / 12 = 1,5 cm.
|
|