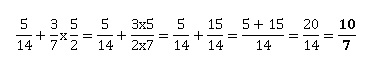QCM. 5 points.
1. Quelle est
l’aire du rectangle ABCD ?
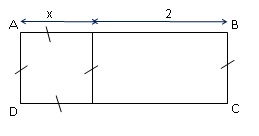
Longueur fois largeur = (x+2) x =
x2 +2x.
2. Alexandra achète
2 cahiers et 3 crayons, elle paie 810 F
Nathalie achète 1 cahier et 5 crayons elle paie 650 F
Combien coûte un cahier et combien coûte un crayon ?
x : prix d'un cahier ; y : prix d'un crayon.
2x+3y = 810 et x+5y = 650 soit x = 650 -5y.
2(650-5y)+3y=810 ; 1300-10y +3y = 810 ; 1300-810 = 7 y ; y =490 / 7 ; y
=
70.
Par suite x = 650 - 5 x70 =
300.
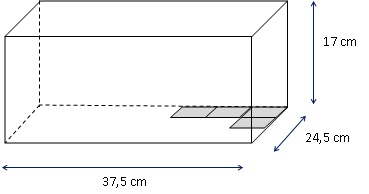
3. À l’entrée du
chemin, sur la première case, sont placés deux cailloux noirs. Le but
du jeu est de sortir du chemin en passant par toutes les
cases.Attention : pour pouvoi r se déplacer sur la case suivante il
faut pouvoir déposer un nombre de cailloux égal au double du nombre de
cailloux sur la case précédente. Combien de cailloux doit-on placer sur
la dernière case ?
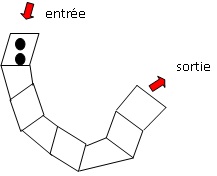 256
256.
4.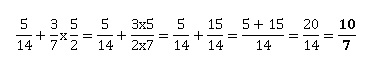 5.
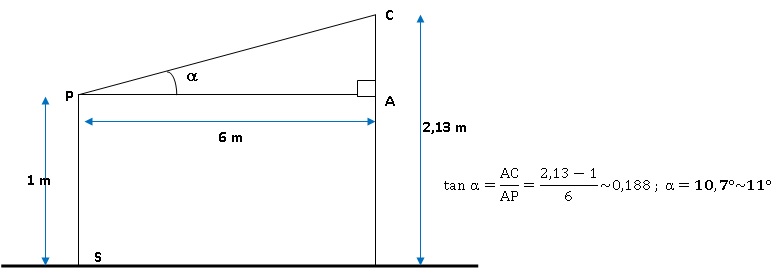
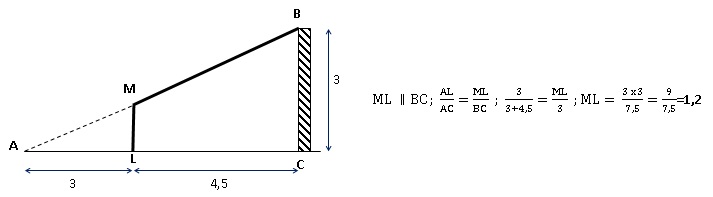
5. Quelle est la
hauteur du poteau ML ?
 Exercice 2
Exercice 2. 7
points.
Voici un programme de calcul :
• Choisir un nombre
• Ajouter 1 à ce nombre
• Calculer le carré du résultat
• Soustraire le carré du nombre de départ au résultat précédent.
• Écrire le résultat.
1. On choisit 4
comme nombre de départ. Prouver par le calcul que le résultat obtenu
avec le programme est 9.
4 +1 =5 ; 5 x5 = 25 ; 25-4
2 = 9.
2. On note x le
nombre choisi.
a. Exprimer le
résultat du programme en fonction de x.
b. Prouver que ce
résultat est égal à 2x +1.
x+1 ;
(x+1)2 ; (x+1)2 -x2 = (x+1-x) ( x+1+x) =
2x+1.
3. Soit f la
fonction définie par f (x) = 2x +1.
a. Calculer
l’image de 0 par f .
f(0) =1.
b. Déterminer par
le calcul l’antécédent de 5 par f .
5 = 2x+1 ; 5-1 = 2x ; x = 2.
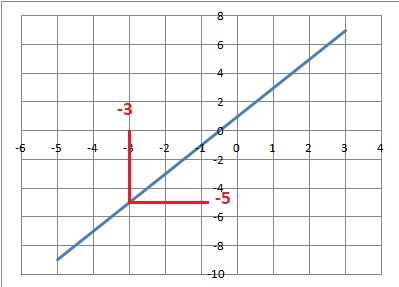
c. Tracer la droite
représentative de la fonction f .
d. Par lecture
graphique, déterminer le résultat obtenu en choisissant −3 comme nombre
de départ dans le programme de calcul. Laisser les traits de
construction apparents.