Mathématiques, concours Audioprothésiste Toulouse. 2016

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.

QCM 1.
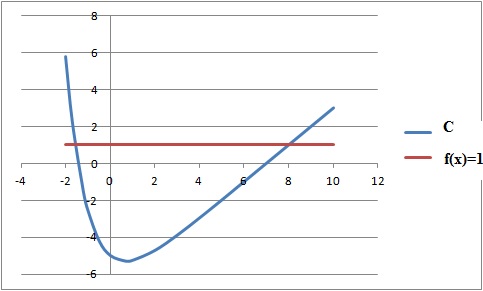
Soit la fonction f définie sur R par f(x) = 2e-x+x-7 et C sa courbe représentative.
 a. La  dérivée de f(x) est f '(x)= 2 e-x+1. Faux.
f '(x) = -2e-x+1.
 b. La fonction f change de variation sur R. Vrai.
f '(x) est négative si x < ln2 ; f(x) est strictement déctroissante.
f '(x) est positive si x > ln2 ; f(x) est strictement croissante.
f '(x) = 0 si x = ln2 ; f(x) présente un minimum égal à f(ln2) = ln2 -7.
c. C admet une asymptote horizontale. Faux.
d. La fonction f admet un maximum. Faux.
e. L'équation f(x)=1 admet une unique solution sur R. Faux.
QCM 2.
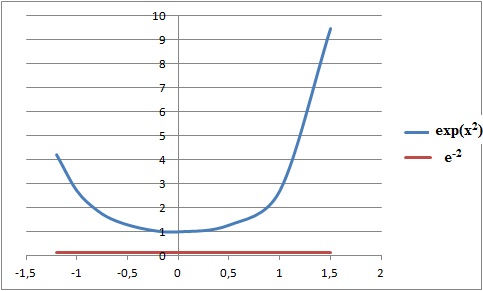
  On considère dans R l'inéquation (1) : exp(x2) < 1/e2.
a. L'inéquation (1) s'écrit ( ex-e-1) (ex+e-1) <0. Faux.
exp(x2) -e-2 <0 ; ln(exp(x2) ) <ln(e-2), la fonction logarithme est strictement croissante sur ]0 ; +oo[.
x2 < -2
 b. Si on pose X = ex alors (1) s'écrit : X2 < 1/e2. Faux.
Ce serait vrai si on avait (ex)2 < 1/e2.
c. (1) est équivalente à x2 < 0,5. Faux.
d. (1) a pour ensemble de solution l'intervalle [ -e-1 ; e-1 ]. faux.
e. (1) n'a pas de solution. Vrai.
QCM 3.
On considère la fonction f définie par f(x) = ln[ (x+2) / (3x)]. On appelle D l'ensemble de définition de f, D' l'ensemble de définition de sa dérivée f '.
a. Pour tout x de D, f(x) = ln (x+2) -ln(x) +ln(3). Faux.
f(x) = ln(x+2) -ln(x) -ln(3).
b. D' est l'ensemble des réels différents de 0 et de -2. Vrai.
f '(x) =1/(x+2) -1/x.
c. f(x) = 0 si et seulement si x=1. Vrai.
f(1) = ln(3 /3) = ln(1) = 0.
0 = ln 1 = ln[ (x+2) / (3x)] ; 1 = (x+2) / (3x) ; x+2 = 3x ; 2x=2 ; x=1.
d. Pour tout x de D', f '(x) = x / (x+2). Faux..
 f '(x) =1/(x+2) -1/x = (x-x-2) / [x(x+2)] = -2 / [x(x+2)]
e. f(-2) = 1. Faux.
f(x) n'est pas définie pour x = -2.
D = ]-oo ; -2 [ union ]0 ; +oo[.
.
 QCM 4.
a. Quand x tend vers + oo, si f(x) tend vers +oo et si g(x) tend vers zéro, alord f(x) *g(x) tend vers zéro. Vrai.
b. Quand x tend vers +oo, si f(x) tend vers +oo et si g(x) tend vers -oo, alors f(x) + g(x) tend vers zéro. Faux.
Par exemple, si f(x) = x2 et g(x) = -x alors f(x) + g(x) tend vers +oo quand x tend vers +oo.
c. Si f et g sont deux fonctions définies sur [0 ; +oo[, la fonction g ne s'annulant pas si, quand x tend vers +oo, f(x) tend vers +oo et g(x) tend vers -oo, alors f(x) / g(x) tend vers -1. Faux
Par exemple, si f(x) = x2 et g(x) = -x+1 alors f(x) / g(x) tend vers +oo quand x tend vers -oo.
d. Si f est une fonction définie sur [0 ; +oo[ telle que 0 < f(x) < x½, alors f(x) / x tend vers zéro quand x tend vers l'infini. Vrai.
0 < f(x) / x < x-½ ;  x-½ tend vers zéro si x tend vers +oo.
e. Quand x tend vers l'infini, si f(x) tend vers -1 et si g(x) tend vers +oo, alors f(x) * g(x) tend vers +oo. Faux.
f(x) * g(x) tend vers -oo.
.
.




QCM 5.
On considère trois suites (un),( vn) et (wn) telles que pour tout entier naturel n non nul, vn <un <wn avec : vn = 3-2/n et
quand n tend vers l'infini, wn tend vers 3.
a. La suite un n'a pas de limite. Faux.
Au voisinage de l'infini vn tend vers 3 en restant inférieur à 3.
b. La limite de un est supérieure à 3 quand n tend vers l'infini. Faux.
La limite de un est inférieure à la limite de wn, c'est à dire 3.
c. On ne peut pas dire si la suite (un) converge. Faux.
d. Quand n tend vers l'infini, la limite de un est égale à 3. Vrai.
e. La suite (un) est décroissante. Faux.
QCM 6.
On considère la suite (un) définie pour tout entier naturel non nul par un = (3n+2) / n.
a. La suite (un) est croissante. Faux.
u1 = 5 ; u2 = 4 ; u3 = 11/3.
b. La suite (un) est minorée par 5. Faux.
La suite (un) est majorée par 5.
c : La suite (un) est divergente. Faux.
Quand n tend vers +oo, un tend vers 3.
 d : Pour tout entier naturel n non nul, un <5. Vrai.
e. La suite un est géométrique. Faux.

 QCM 7.
Soit la fonction h définie sur R par h(x) = sin(2x).
  a. La fonction dérivée h'(x) est égale à cos(2x). Faux.
h'(x) = 2 cos(2x)..
 b. La fonction h est paire. Faux.
h(-x) = - sin(2x) = -h(x).
c. La fonction H définie par H(x) = sin2(x) est une primitive de h(x). Vrai.
H'(x) = 2 sin(x) cos (x) = sin(2x)
d. h(p/6)=0,5. Faux.
sin (p/3) ~ 0,866.
e. Pour tout réel x de [0 ; p], h(x) >0. Faux.
Par exemple sin (2 x 120) ~ -0,866.









QCM 8
Soient f et g les fonctions définies pour tout x réel par :
f(x) = 5x4 +3x2+1 et g(x) = x exp(x2). Alors.

QCM 9.
Soit x un réel strictement supérieur à 1, alors

QCM 10.
Le plan complexe est muni d'un repère orthonormé direct d'origine O. Soit z un nombre complexe non nul d'argument q.
Un argument de z' est :

QCM 11.
Soit z1 et z2 les nombres complexes solutions de l'équation z2 -4z+6=0. Dans le plan complexe muni d'un repère orthonormé direct d'origine O, on considère les points M1 et M2 d'affixes respectives z1 et z2 puis I le milieu du segment [M1M2].
a. Le nombre z1+z2 est un imaginaire pur. Faux.
D = (-4)2 -4x6 = .-8 = 8 i2.
z1 = 2 + 2½i ; z2 = 2 - 2½i ; z1 + z2 = 4
b. L'affixe du point I est un imaginaire pur. Faux
(z1 + z2 ) /2= 2.
c. Le nombre z1 x z2 est égal à 2. Faux
(2 + 2½i)(2 - 2½i) =4+2=6.
d. Les droites (OI) et (M1M2) sont perpendiculaires. Vrai.
Coordonnées du vecteur directeur de la droite (OI) : 2 ; 0.
Coordonnées du vecteur directeur de la droite (M1M2) : 0 ; -2x2½.
Le produit scalaire de ces deux vecteurs directeurs est nul.

e. Le triangle OM1M2 est équilatéral. Faux.
OM1 = OM2 = (4+2)½ ; M1M2 =(0+8)½.




QCM 12.
L'espace est rapporté à un repère orthonormé. On donne les points A(2 ; 1 ; 0), B(6 ; -7 ; -4).
P est le plan d'équation 4x+y+5z+3 = 0 et (D) la droite de représentation paramétrique x=1 +2t ; y = -2-3t ; z = -1-t, t réel.
a. Le plan P contient la droite (D). Vrai.
4(1+2t) -2-3t-5-5t+3 = 0 est vérifiée quel que soit t.
 b. B n'appartient pas à P. Faux.
4 x6-7+5x(-4)+3= 0 est vérifié.
c. B appartient à (D). Faux.
6 =1+2t soit t = 2,5 ; y = -2-3x(2,5)=-9,5 différent de yB.
 d. La droite (D) est  strictement parallèle au plan P. Faux.
(D) est contenue dans P
e. La droite (D) est sécante au plan P en A. Faux.
A n'appartient pas à la droite (D).
QCM 13.
Une urne contient 75 boules blanches et 25 boules noires. On tire une boule, toutes les boules ont la même probabilité d'être tirées.
On effectue n tirages indépendants avec remise, n est un entier supérieur à 10.
Soit X la variable aléatoire prenant pour valeur le nombre de boules blanches tirées.
a. X suit une loi binomiale de paramètres n et 0,25. Faux.. Faux.
Le succès " tirer une boule blanche " est tel que  p = 0,75.
b. P(X=0) = 1 / 22n.  Vrai.
P(X=0)= Cn0 p0 qn =0,25n =1/4n=1/22n .
c. P(X <5) = 1 -P(X >5). Faux.
Il faudrait écrire P(X<5) ou P(X>5) pour que ce soit vrai.
d. E(X) = 0,5 n. Faux.
E(X) = n p = 0,75 n..
e. La loi B( n ; 0,75) peut être approchée par la loi N(0,75 n ; 0,1875n) dès que n >10. Faux.
n > 30 ; np >5 et n q >5.
QCM 14.
La durée d'attente en seconde à la caisse d'un supermarché suit une varaible aléatoire Y qui suit la loi exponentielle de paramètre 0,01.
a. La densité de probabilité de Y est la fonction f définie sur [0 ; +oo[ par f(t) = e-0,01t. Faux.
f(t) = 0,01 e-0,01t.
b. Pour tout t réel positif, P(Y< t) = e-0,01t. Faux.
P(Y< t) =1- e-0,01t.
c. La probabilité d'attendre moins de 3 minutes à cette caisse est égale à 1-e-0,03. Faux.
Il faut exprimer le temps en secondes.
d. PY>60(Y>180) = P(Y >120). Vrai.
La loi exponentielle modèlise la durée de vie d'un phénomène sans mémoire. Le fait que le phénomène ait duré pendant t heures ne change rien à son espérance de vie à partir de l'instant t.
 PY>60(Y>180) = P(Y >120).
e. L'espérance de Y est égale à 10. Faux.
E(Y) = 1 /0,01 = 100 secondes.
QCM 15.
X est la variable aléatoire qui suit la loi N(0 ; 1).
a. P(-2 < X <2) ~0,99. Faux.
Les tables donnent F(2) = 0,9772 ; P(-2 < X <2) = 1-2(1-0,9772)=0,9544.
b. P(-2 < X <2) ~0,95. Vrai.
c. P(-2 < X <2) ~0,68. Faux.
d. P(X <2) ~0,96. Faux.
e. P(X < 2 ) =1-P(X >-2).Faux.


  

menu