Mathématiques,
concours Avenir 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Les complexes.
1. Le nombre complexe i est :
a. nul.
b. négatif.
c. positif
d.
aucune des trois propositions ci-dessus n'est correcte. Vrai.
Les parties réelle ou imaginaire d'un nombre complexe peuvent être positive, négative ou nulle.
Un nombre comples ne peut pas être positif négatif. La partie imaginaire de i est positive ( +1)
L'équation z3+z=0 admet :
2. Dans R :
a. 0 solution ; b. 1 solution vrai ; c. 2 solutions ; d. 3 solutions.
(z2+1) z = 0 ; dans R, une solution z = 0.
3. Dans C :
a. 0 solution ; b. 1 solution vrai ; c. 2 solutions ; d. 3 solutions. Vrai.
(z2+1) z = 0 ; dans C, z = 0 et z2=-1= i2 , soit z = ±i.
Soient, dans un repère orthonormé direct du plan complexe, les points A, B, C et D
d’affixes respectives : 4+i ; −2−i ; 2+3i et 1.
4. Le triangle ABC est :
a. rectangle en A; b. rectangle en B ; c. rectangle en C ; vrai
d. aucune des propositions précédentes n'et correcte.
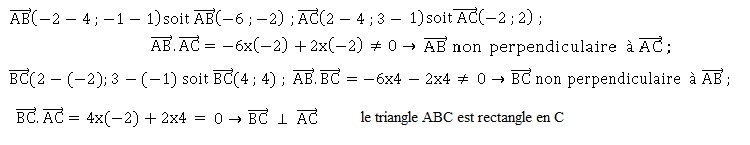
5. Un argument du nombre complexe Z suivant correspond à une mesure de l'angle orienté :
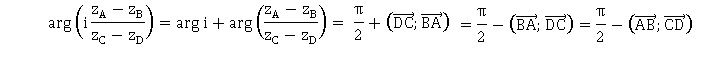
Réponse c.
6. Le module du nombre complexe Z défini précédemment est :
a : i AB / CD.
b : i CD / AB.
c : AB / CD. Vrai.
d : CD / AB.
|i| |zA-zB| / |zC-zD| = 1 |zA-zB| / |zC-zD| = AB / CD.
7. L'écriture algébrique de ce nombre complexe Z est :
a : 9 /5 +3i /5. b : 8 /5 +6i /5. Vrai.
c :-2+2i. d : aucune des trois propositions ci-dessus n'est correcte.
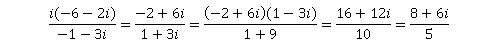
8. Le point D appartient au segment :
a : [AB] vrai ; b :[AC]. c : [BC].
d : aucune des trois
propositions ci-dessus n'est correcte.
ZAD=zD-zA =-3-i ; ZAB=zB-zA =-6-2i =2ZAD
|
| .
. |
|
|
Interprétations graphiques.
Ci-dessous les courbes C et S représentant respectivement les fonctions f définie sur R−{3} et
g ′ définie sur R.
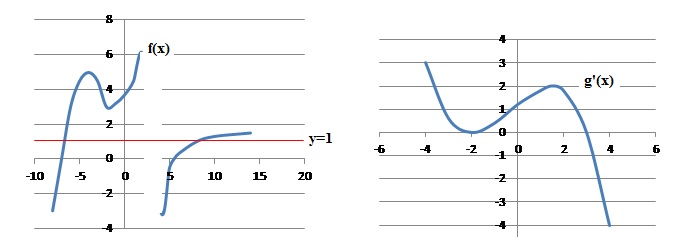
9. Quand x tend vers 3, la limite de f(x) est :
a : -oo. b : +oo. c
: un réel. d : aucune
des réponse précédentes.
Vrai.
Quand x tend vers 3 par valeur inférieure, f(x) tend vers plus l'infini.
Quand x tend vers 3 par valeur supérieure, f(x) tend vers moins l'infini.
La limite en 3 n'existe pas.
10. Le nombre de solutions de l'équation f(x)=1 est :
a :
0.. b :
1. c :2. Vrai. d : 3.
x=7 et x=-7, intersections avec la courbe et la droite y=1.
11. Le nombre de
solutions de l'équation f '(x)=1 est
:
a :
0.. b :
1 Vrai. c :2. d : 3. Vrai.
Tracer les tangentes à la courbe dont le coefficient directeur est égal à 1.
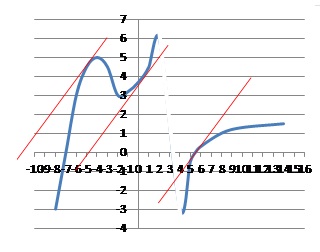
12. Le nombre de solutions de l'équation f '(x) x g'(x)=0 est :
a. 0. b. 1. c : 2. vrai. d : 3.
f '(x) s'annule pour x = -4 ; en x=-2, il y a un point anguleux ; en ce point, f(x) n'est pas dérivable.
g'(x) s'annule pour x = -2 et x = 3, mais f(x) n'est pas définie pour x=3.
f '(x) x g'(x)=0 admet donc deux solutions x= -4 et x = -2.
13. Sur [-2 ; 3[ union ]3 ; +oo[ la fonction f est :
a. constanter. b. strictement décroissante.
c. strictement croissante.
d. aucune des
solutions précédentes. Vrai.
Si un fonction est croissante sur un intervalle, alors si a <b, f(a) < f(b) quel que soient a et b.
Prenons a = 0, f(0)=3,6 ; b = 4, f(4) = -3.
14.
Sur [-2 ; 3] la fonction g est :
a. constante ; b. strictement décroissante ; c. strictement croissante. Vrai ; d.
aucune des réponses précédentes.
g'(x) est positive sur cet intervalle ; g(x) est strictement croissante sur [-2 ; 3 ].
15. 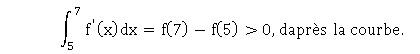 Réponse c. Réponse c.
16 . 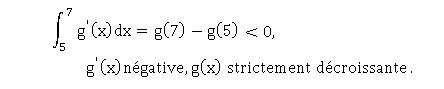 Réponse b. Réponse b.
Fonctions.
Soient : f la fonction définie sur R par f (x) = 2e−3x −4x +6cos(0,5x),
f ′ sa fonction dérivée et F sa primitive s’annulant en 0.
17. Quand x tend vers -oo, la limite de f(x) est :
a. -oo ;
b. +oo, vrai . c. n'existe pas ; d.
aucune des propositions précédentes.
Quand x tend vers moins l'infini : 2e−3x tend vers +oo ; -4x tend vers +oo ; la limite de cos(0,5x) n'existe pas mais ce terme reste compris entre -1 et +1.
|
|
|
|
18. Quand x tend vers +oo, la limite de f(x) est :
a. -oo, vrai ;
b. +oo . c. n'existe pas ; d.
aucune des propositions précédentes.
Quand x tend vers plus l'infini : 2e−3x tend vers 0 ; -4x tend vers -oo ; la limite de cos(0,5x) n'existe pas mais ce terme reste compris entre -1 et +1.
19. La dérivée est
définie par f '(x) = :
a. 2e−3x −4 +6sin(0,5x) ; b. 2e−3x −4 -6sin(0,5x) ; c. -6e−3x −4 +3sin(0,5x) ;
d. -6e−3x −4 -3sin(0,5x). Vrai.
20. Le nombre de solution de f(x)=0 est :
a. 0 ; b. 1 Vrai; c. 2 ; d. aucune des
proposition proposée.
f '(x) <0, donc f(x) est strictement décroissante sur R.
Quand x tend vers -oo, f(x) tend vers l'infini ; quand x tend vers +oo,
f(x) tend bers -oo. D'après le théorème des valeurs
intermédiaires, f(x)=0 admet une seule solution.
21. La plus petite solution de l'équation f(x)=0 est :
a. strictement négative ; b. strictement positive vrai ; c. nulle ; d. Aucune des trois
propositions proposées n'est correcte.
f(0)= 2+6=8 ; f(x) est strictement positive.
22. Pour tout x réel, F(x) = :
a. 2e−3x −2x2 +6sin(0,5x) ; b. 2e−3x −2x2 +6sin(0,5x)-2 ; c. -2/3 e−3x −2x2 +12sin(0,5x) ;
d. Aucune des trois
propositions proposées n'est correcte. Vrai.
-2/3 e−3x −2x2 +12sin(0,5x) est bien une primitive de f(x), mais elle ne s'annule pas pour x=0.
23.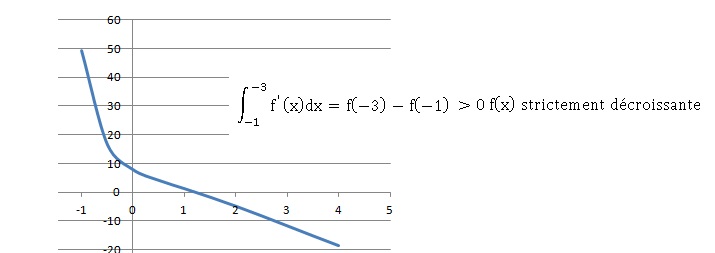
Réponse c.
24. 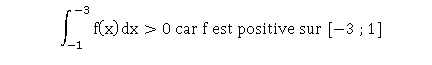 Réponse c. Réponse c.
25. f est une fonction :
a. à la fois paire et impaire ; b. paire non impaire ; c. impaire non paire ;
d. aucune des propositions
précédentes. Vrai.
26. f est :
a. périodique de
période 2p.
b. périodique de
période p.
c. périodique de
période p/2.
d. aucune des
propositions précédentes. Vrai.
Suites.
Soient les suites : (Un) définie par U0 = 4 et pour tout entier naturel n : Un+1 = −1,5 Un+2,5n+1.
et (Vn) par Vn =Un −n.
27. U2= :
a. 11. Vrai
b. 39 /4.
c. -5.
d. aucune des
propositions précédentes.
U1 = -1,5 x4+2,5x0+1= -5. U2 = -1,5 x(-5) +2,5 x1+1 =11.
28. (Un) est :
a. arithmétique et géométrique ; b. arithmétique non géométrique ; c. géométrique non arithmétique ;
d. aucune des
propositions précédentes. Vrai
Les seules suites à la fois arithmétique et géométriques sont les suites constantes..
29. (Vn) est :
a. arithmétique et géométrique ; b. arithmétique non géométrique ; c. géométrique non arithmétique ; Vrai
d. aucune des
propositions précédentes.
Vn+1 =Un+1-(n+1)= −1,5 Un+2,5n+1-n-1=−1,5 Un+1,5 n =-1,5 ( Un -n)= -1,5 Vn.
30. Quel que soit n, Un= :
a. 4x(-1,5)n-n.
b. 4x(-1,5)n.
c. 4x(-1,5)n+n. Vrai.
d. aucune des
propositions précédentes.
Un =Vn+n=(-1,5)n V0+n=4(-1,5)n +n.
31. La suite (Un) :
a. converge.
b. diverge vers -oo.
c. diverge vers +oo.
d. aucune des
propositions précédentes. Vrai.
Cette suite n'a pas de limite.
32. 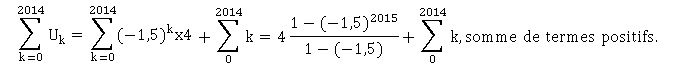
Réponse c.
|
|