QCM
Mathématiques,
suites, nombres complexes, exponentielle, probabilités, concours Avenir
2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Raisonnement.
Pour les questions 1 à 5 on
considère une opération notée +
et définie par :
Pour tous réels a et b on A : a+ b = a + 2x ax b + b, où + et désignent
respectivement l’addition et la multiplication dans R.
1. (-2)+ (5+0,5)=
A) -59 / 2
B) 109 / 2
C) -67 / 2
D) 101 / 2
(5+0,5)= 5 +2x5 x0,5 +0,5 = 10,5.
(-2)+ (5+0,5)= -2+2 x(-2)x10,5 +10,5 = -33,5 = -67
/ 2.
2. Question 2 :
Parmi les 4 propositions suivantes, laquelle est vraie ?
A : Si a > -1 alors a + a > 0.
B : Si a <-1 alors a + a > 0.
C : Si a < 0 alors a
+ a < 0.
D : Si a < 0 alors a
+ a > 0.
a + a = a + 2a2+a = 2a2
+ 2a= 2 a(a+1).
3. On
dit que l’opération +
admet pour élément neutre le nombre réel
noté ne si pour tout réel a on a : a +
ne = ne+ a = a. Alors
A : ne = 0
B : ne = 1
C : ne = -1
D : ne est égal à une autre valeur que les trois proposées
aux réponses précédentes.
a+ ne = a + 2x ax ne + ne = a ; 2x ax ne + ne =0 ; ne(1+2a)=0
; ne = 0.
4. On dit qu’un nombre réel a
admet pour symétrique pour l’opération + le nombre noté a si a =a + a = ne,
où ne est le nombre défini à la question 3. S’il existe,
alors a =
A :-a
B : (2a-1) / a
C
: -1 /a
D : -a /(1+2a).
a
+ a =
0 ; a+ a = a + 2x ax a + a =0 ; a(1+2a) = -a ; a= -a /(1+2a).
5. Dans R,
l’équation a+ 1 = a x a admet
A : aucune solution
B : exactement une solution
C : exactement deux
solutions
D : un nombre de solutions qui dépend de la valeur de a
a + 1 =
a2 ; a+ 1 = a + 2x ax
1 + 1 =a2 ; 3a+1=a2 ; a2
-3a-1=0 ; D =9+4
= 13.
Le discriminant étant positif, l'équation
a+ 1 = a x a admet exactement deux solutions.
Algorithmique
Pour les questions 6 à 9 on considère l'algorithme suivant :
Variables : I , , U: nombres
Traitement :
Saisir un entier N
Saisir un nombre U
Affecter à I la valeur 0
Tant que I < N faire
Affecter à I la valeur I+1
Affecter à U la valeur U +0,5 I xU
fin du tant que
Afficher U
6. Si on fait
fonctionner l'algorithme avec N = 3 et U =2 , on obtient comme affichage
A : 15
B : 4
C : 6
D : Aucune des réponses précédentes n’est exacte.
I
|
0
|
1
|
2
|
3
|
N
|
3
|
3
|
3
|
3
|
U
|
2
|
2+0,5
x1x2=3
|
3+0,5
x2x3= 6
|
6+0,5x3x6=15
|
I
< N
|
vrai
|
vrai
|
vrai
|
faux
|
7. Si
on désire remplacer la boucle « tant que » par une boucle « répéter »
on doit écrire
A
: pour I allant de 0 à N par pas de 1
Affecter à I la valeur I+1
Affecter à U la valeur U+0,5 xIxU
Fin du pour |
B
: pour I
allant de 0 à N-1 par pas de 1
Affecter à I la valeur I+1
Affecter à U la valeur
U+0,5 xIxU
Fin du pour |
C
: pour I
allant de 1 à N par pas de 1
Affecter à I la valeur I+1
Affecter à U la valeur
U+0,5 xIxU
Fin du pour |
D
:
Aucune des réponses précédentes
n’est exacte. |
8. Si on désire remplacer la boucle
« tant que » par une boucle « pour » on doit écrire
A
: Répéter
Affecter à I la valeur I+1
Affecter à U la valeur U+0,5 xIxU
Jusqu’à I < N |
B
: Répéter
Affecter à I la valeur I+1
Affecter à U la valeur U+0,5 xI xU
Jusqu’à I = N-1 |
C
: Répéter
Affecter à I la valeur I+1
Affecter à U la valeur U+0,5 xI xU
Jusqu’à I > N |
D
:
Aucune des réponses précédentes
n’est exacte. |
9. La variable U contient les
termes successifs de la suite (un) définie par
A : u0 = 2 : un+1 =0,5 n x un pour
tout entier naturel n.
B : u0 = 2 : un+1 =un+0,5
n x un-1 pour tout entier naturel n.
C : u0 = 2 : un+1 =un+(n-1)0,5
n x un-1 pour tout entier naturel n.
D : Aucune des réponses
précédentes n’est exacte.
u1 doit être égal à 3. A
conduit à u1 = 0 ;
u2
doit être égal à 6. B conduit
à u2 = 3+2 ; conduit à : u2
=3+0.
|
|
.
.
|
|
|
Suites.
10) On
considère la suite (un) définie par u0 = 5 et un+1=un+4
pour tout entier naturel, alors u23=
A : 119
B : 85
C : 97
D : 111
Suite arithmétique de
premier terme 5 et de raison 4 : u23
= 5 +23 x4 = 97.
11) On considère
la suite (un) définie par un =(-1)n x
E(n/3) / (n2+n+1) , où E(x) désigne la partie entière de x,
alors
A : (un) n’est ni minorée, ni majorée.
B : (un) est minorée mais pas majorée.
C : (un) est majorée mais pas minorée.
D : est bornée.
La présence de (-1)n élimine les propositions B et C.
Quand n devient grand, (un)
, u2n tend vers zéro par valeur positive et u2n+1
tend vers zéro par valeur négative.
12. On considère une suite (un)
arithmétique de raison 3 et une suite (vn) arithmétique de
raison 2, alors la suite (wn) définie par wn=un+vn
vn est
A : arithmétique de raison 6.
B : géométrique de raison 5.
C : arithmétique de raison .
D : arithmétique de raison
5.
un+1
=3+ un ; vn =2 + vn ; wn
=5 + vn +un.
13) On considère
une suite géométrique (un) de raison 3 et une suite
géométrique (vn) de raison 2, alors la suite alors
la suite (wn) définie par wn=un x vn vn
est
A : géométrique de raison 6.
B : géométrique de raison 5.
C : géométrique de raison 9.
D : géométrique de raison 8.
un+1 =3 un ; vn+1 =2 vn ; wn
=6 vn un
14)
On considère une suite (un) géométrique de raison 3 et une
suite (vn) géométrique de raison 2, alors la suite (wn)
définie par wn = 0,5(un+vn) est
A : géométrique de raison 2,5.
B : arithmétique de raison2,5 .
C : arithmétique de raison 4,5.
D : ni arithmétique, ni
géométrique.
un+1 =3 un ; vn+1 =2 vn ; wn
=0,5(3un + 2vn).
Nombres complexes.
15) On
considère le nombre complexe z = 3 i , alors z4 =
A : 81 i
B : -81
C : -81 i
D : 81
z = 3 exp(ip/2) ; z4
= 34 exp(2ip) = 81.
16) Les nombres réels a et b tels
que pou tout z complexe, z3 +(2-i) z2
+(1-2i)z-i=(z-i)(z2+az+b) sont :
A) a=-2 et b = 1
B) la = -2 et b =-1
C) a = 2 et b = -1
D) a=2 et b = -1.
(z-i)(z2+az+b)=z3 +(a-i)
z2 +(b-ai)z-bi =z3 +(2-i) z2
+(1-2i)z-i.
On identifie : b = 1 ; a
= 2.
17) exp(ip/2) [6exp(ip)+2] / (2i )=
A) -2
B) 2+i
C) 0
D) 2.
exp(ip/2) / i = 1 ; exp(ip) = -1 ; exp(ip/2) [6exp(ip)+2] / (2i )=0,5 (-6+2) = -2.
18) On considère le nombre complexe
z = (2 +2i) / (3½+i), alors un argument à 2 p près de z est :
A) -p /12
B) p /12
C) 5p /12
D) -5p /12
z = (2+2i)( 3½-i) /
2 =(1+i)(( 3½-i) ; 1+i = exp(ip/4) ; 3½-i =2 exp(-ip/6) ; z = 2 exp(i(p/4-p/6)) = 2 exp(ip/12).
19) On considère le
nombre complexe z = 5½ exp(3ip/4), alors un
argument de la moyenne arithmétique de z et de son conjugué est
A) 0.
B) p/2
C) p.
D) 3p/2.
z + z =2 fois
la partie réelle de z = 2 x 5½ cos (3p/4) = -10½.
20) On se place
dans le plan complexe muni d’un repère orthonormé. L'affixe du vecteur
suivant est :
A) 10 exp(ip/3).
B) 5 exp(-ip/3)
C)
5½ exp(-ip/3)
D) 10 exp(-ip/3).
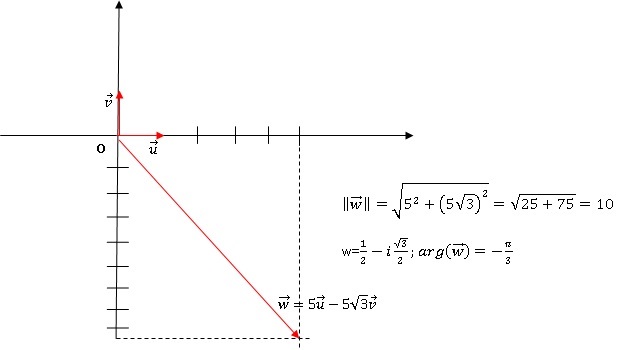
|
|
|
|
|
21) On se place dans le plan
complexe muni d’un repère orthonormé , les images des solutions de
l’équation z4=6 sont
A : les sommets d’un triangle équilatéral.
B : les sommets d’un carré.
C : les sommets d’un pentagone régulier.
D : les sommets d’un hexagone régulier.
On pose Z = z2
; Z2 = 6 : Z= +6½ et
Z = i26½
z =
±60,25 et z = ± i 60,25
.
Probabilités
conditionnelles
Pour les questions 22 à 24 on considère l’arbre pondéré suivant :
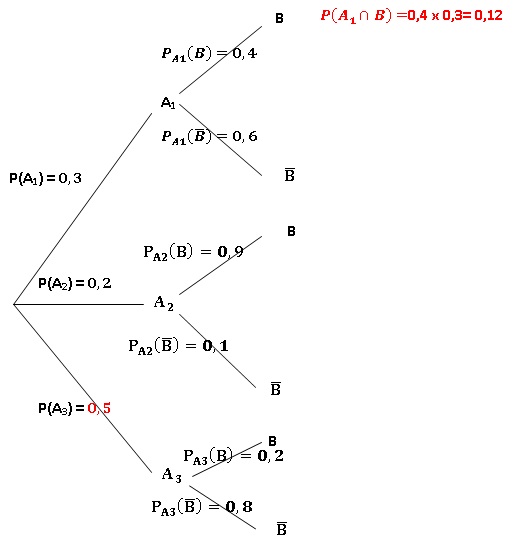
22)
P(A3)=
A) 0,1
B) 0,2
C) 0,5
D)
0,498.
23.
P(A1 n B)=
A) 0,1
B) 0,12
C) 0,18
D) 0,4
24.
Les évènements A1 et B et sont
A : incompatibles.
B : certains.
C : dépendants.
D : indépendants.
Lecture
graphique
Pour les questions 25 à 28 on se place dans le plan
muni d’un repère orthonormé. On a tracé la courbe représentative d’une
fonction dérivable et strictement décroissante sur R. Le point M est le
point de la courbe d’abscisse 0. La droite (MC) avec C ( 2,5; 0) est la
tangente à la courbe au point d’abscisse 0. Le point M et le point A (2
;1) sont situés sur le même cercle dont le centre est l’origine du
repère.
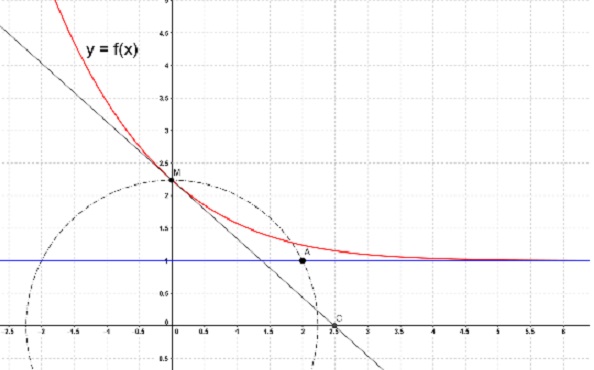
25)
La courbe représentative de f admet
A : la droite d’équation x = 1 comme asymptote horizontale en + ∞.
B : la droite d’équation y
= 1 comme asymptote horizontale en + ∞.
C : la droite d’équation x = 1 comme asymptote verticale en + ∞.
D : la droite d’équation y = 1 comme asymptote verticale en + ∞.
26)
La valeur exacte de est f(0) est :
A) 21 / 10
B) e
C) 5½
D) 3 x3½ / 2.
OM = OA = (22+12)½
= 5½.
27)
Un vecteur directeur de la droite (MC) a pour coordonnées :
A) -5½ ; 2
B) -5½ ; 2
x 5½
C) -5½
; -2 x 5½
D) -5 ; 2 x 5½
Coordonnées du vecteur MC
: xC-xM = 2,5 -0 = 2,5 ; yC-yM = 0 -5½
= -5½ ;
Coordonnées d'un vecteur colinéaire au vecteur OM : -2 x5 ; -2
x(-5½).
28)
La fonction représentée est f(x) = (1+ae-x)½
avec a =
A) 3½
B) 5½
C) 4
D) 1,5.
f(0) =(1+ae0)½
=(1+a)½ =5½ .
Trigonométrie.
Pour les questions 29 à 31 on considère la fonction cotangente notée
cotan(x) et définie par cos(x) / sin (x).
29) cotan(p/4)=
A) 1
B) 0
C) 2½
D) 3½.
cos (p/4)
/ sin (p/4)
= 1.
30.
la fonction cotangente n'est pas définie si :
A) x = p /2 +2kp où k est un entier
relatif.
B) x = p /2 +kp où k est un entier
relatif.
C)
x = 2kp où k est
un entier relatif.
D) x =kp où k est un entier relatif.
sin(x) doit être
différent de zéro.
31.
Pour tout appartenant à son domaine de définition, la fonction
cotangente est dérivable et admet pour fonction dérivée :
A) 1 +(cotan(x))2.
B) 1 / sin2(x).
C) -1 / sin2(x).
D) (cotan(x))2-1.
On pose u = cos(x) et v = sin(x) ; u' = -sin(x) ; v' = cos(x).
(u'v-v'u) / v2 = (-sin2(x) -cos2(x)) /
sin2(x) = -(sin2(x) +cos2(x)) /
sin2(x) = -1 /sin2(x)
|
|
Fonction
exponentielle.
32) e5x e-3
/ (e3)2 =
A) e-3.
B) e-15 /6.
C) e-4.
D) e9.
e(5-3) / e6
= e2-6=e-4.
33) Les solutions dans de
l’équation e2x+ex-2=0 sont :
A) -2 et 1.
B) 0
C) e-2 et e.
D) Aucune des réponses précédentes n'est juste.
On pose X = ex
positif ; X2+X-2 = 0 ; D = 1+4x2 = 9 ; X = (-1+3) / 2 = 1 ; ex=1
; x = 0.
34) Quand x tend
vers plus l'infini, la limite de exp(x3-3x+9)½) =
A) plus l'infini
B) zéro
C) exp(x1,5)
D) e3.
35) Pour tout
nombre réel non nul ex / x4 =
A) e4y / (16y4) avec y = 4x.
B) (ey /
y)4 / 256 avec x = 4y
C) e4y / (16y4) avec x = 4y.
D) (ey / y)4 / 64 avec x = 4y.
On pose x = 4y : e4y
/ (44.y4 )= (ey)4
/ (256.y4) =(ey
/ y)4 / 256.
36). On considère
la fonction f définie surR par : f(x) = cos(3x) e-2x.
La fonction dérivée de f en x est
A : -e-2x(3
sin(3x) +2 cos(3x)).
B : -3e-2x(3
sin(3x) +2 cos(3x)).
C : -2e-2x(3 sin(3x) +2 cos(3x)).
D : -e-2x(3 sin(3x) -2 cos(3x)).
On pose u = cos(3x) et v
= e-2x ; u' = -3 sin(3x) ; v' = -2e-2x.
u'v+v'u = -3e-2xsin(3x)
- 2e-2xcos(3x) = -e-2x(3
sin(3x) +2 cos(3x)).
37) Quand x tend
vers zéro, la limite de (e3x+2-e2) / x est :
A) plus l'infini.
B) zéro.
C) e2 / 3.
D. 3 e2.
e2(e3x-1)
/ x ~ e2(1+3x-1)
/ x = 3e2.
|
|
|