QCM
Mathématiques, logarithme népérien, intégration, géomtrie dans
l'espace,lois de probabilités, concours Avenir
2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Fonction logarithme népérien.
38. Dans R l’équation ln(x+3)+ln(x+2)=0 admet
A : aucune solution.
B : une solution.
C : deux solutions.
D : Aucune des réponses précédente n'est juste.
x +2 doit être positif ; x+3 doit être positif ;soit x > -2.
ln((x+3)(x+2))=0 = ln 1 ; (x+3)(x+2) = 1 ; x2+5x+5=0 ; D = 52-20 = 5.
seul x = (-5 +5½) / 2 convient.
39. ln (8e5)=
A : 3 ln(2)+e5.
B : 3 ln(2) + 5e.
C : 15 ln(2e).
D : 5 + 3ln(2).
ln23 + ln(e5) = 3 ln2 +5.
40. La fonction f définie sur R par : f(x) = ln((1+3ex)½+e) est
A : strictement croissante sur R.
B : strictement décroissante sur R.
C : croissante sur ]-oo ; 0] puis décroissante sur [0 ; +oo[.
D : décroissante sur ]-oo ; 0] puis croissante sur [0 ; +oo[.
On pose u = (1+3ex)½+e ; u' = 3(1+3ex)-½ positif.
f '(x) = u ' / u = 3(1+3ex)-½ / ((1+3ex)½+e) positive.
41. Quand x tend vers 2+, la limite de ln(x-2) / (6-x-x2) est :
A : moins l'infini
B : zéro
C
: plus l'infini.
D : Aucune des réponses précédentes n’est juste.
(6-x-x2) = (x-2) (x-3) ; ln(x-2) / (6-x-x2) = [ ln (X) / X ] / (X-1) avec X = x-2.
Quand X tend vers 0+, ln (X) / X tend vers moins l'infini et (X-1) tend vers -1.
42. Quand x tend vers plus l'infini, la limite de (1+ln(x)) / (4x) est :
A : moins l'infini
B : zéro
C : plus l'infini
D : Aucune des réponses précédentes n’est juste.
Qund x tend vers plus l'infini, 1 /(4x) tend vers zéro et ln(x) / x tend vers zéro.
43. Pour tout x >0, l'équation [ln(x+2) +3 ] / x =5 est équivalente à :
x = 0,5(e5x+3).
B : x=e5x-5.
C : x=e5x-3 -2
D : Aucune des réponses précédentes n’est exacte.
ln(x+2) +3 = 5x ; ln(x+2) = 5x-3 ; x+2 = e5x-3 ; x = e5x-3-2.
44 . Soit n un nombre entier naturel, l’inéquation 5-(3 / 4)n > 3 est équivalente à :
A. n < (ln(3)-ln(5)) / (ln(3)-ln(4)).
B. n > ln(2) / (ln(3)-2 ln(2)).
C. n > ln(2) / (ln(4)- ln(3)).
D : Aucune des réponses précédentes n'est juste.
(3/4)n < 2 ; n ln(3/4) < ln(2) ; n < ln(2) / (ln(3)-ln(4)) avec ln(4) = ln(22) = 2 ln(2).
|
|
.
.
|
|
|
|
Intégrations.
45.
On se place dans le plan muni d’un repère et on considère la fonction f
positive de courbe représentative C, alors pour a et b réels tels que a
≤ b, 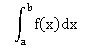 est est
A : l’aire de la surface délimitée par l’axe des abscisses, C, les droites d’équation y = a et y = b.
B : l’aire de la surface délimitée par l’axe des abscisses, C, les droites d’équation x = a et y = b.
C : l’aire de la surface délimitée par l’axe des abscisses, C, les droites d’équation y = a et x = b.
D : l’aire de la surface délimitée par l’axe des abscisses, C, les droites d’équation x = a et x = b.
46. 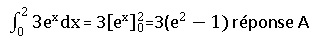
47. Soit f une fonction continue sur R, alors :
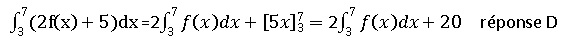
48. 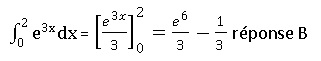
Géométrie dans l'espace.
Pour les questions 49 à 52 on se place dans l'espace muni d'un repère orthonormé.
49.
On considère la droite (d) passant par A(2 ; 3 ; -1)et de vecteur
directeur de coordonnées (2 ; -1 : 1) alors une représentation
paramétrique de (d) est :
A : x = 2-t ; y = 3+2t ; z = -1+t avec t réel.
B : x = 2+2t ; y = 3-t ; z = -1+t avec t réel.
C : x = 2+2t ; y = -1+3t ; z =1-t avec t réel.
D : x = 4+2t ; y = 6-t ; z = -2+t avec t réel.
50. On considère le plan P d’équation cartésienne x-2y+z+1=0 alors un repère du plan P est :

51.
On considère le plan P d’équation cartésienne 2x+3y+z+2=0 et la droite
(d)de représentation paramétrique x = 4-2t ; y = 1+t ; z = 2-t où t est
réel, alors :
A : le plan P contient la droite (d).
B : le plan P ne contient pas la droite (d) et la droite est parallèle au plan .
C : le plan P et la droite (d) sont sécants et non perpendiculaires.
D : le plan P et la droite (d) sont perpendiculaires.
Coordonnées d'un vecteur normal au plan P ; (2 ; 3 ; 1 )
Coordonnées d'un vecteur directeur de la droite (d) :( -2 ; 1 ; -1 ).
Ces deux vecteurs ne sont ni colinéaires ni orthogonaux.
2(4-2t) +3(1+t)+2-t+2 = 0 ; 8-8t +3+3t +2-t+2 = 0 ; t = 15 / 6 = 5 / 2. La droite et le plan sont sécants.
52.
On considère le plan P d’équation cartésienne x+2y-z+4=0et la droite
(d) de représentation paramétrique x = 1-t ; y = t ; z = 2 où t est
réel, alors(d) coupe P au point de coordonnées
A : (4 ; -3 ; 1)
C : (4 ; -2 ; -4)
C : (1 ; -3 ; 2)
D : (4 ; -3 ; 2)
1-t +2t-2+4=0 ; t = -3. ; x=1-(-3) = 4 ; y = -3 ; z = 2.
Loi de probabilités
Pour les questions 53 à 55 on considère une variable aléatoire continue
X, à valeurs dans [-2 ; 2] dont la densité de probabilité est
représentée ci-dessous.
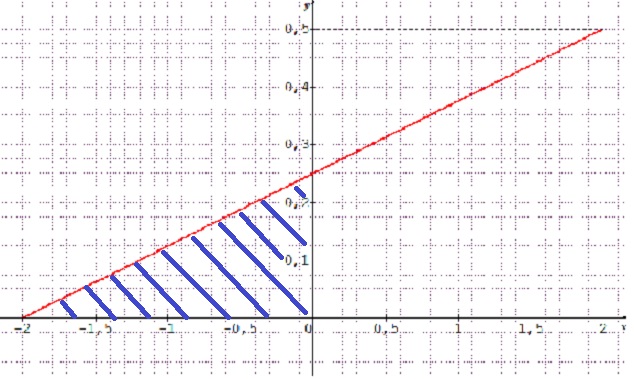
53 P(X ≤ 0) =
A : 0
B : 0,25
C : 0,125
D : 0,5
2 *0,25 / 2 = 0,25 ( aire hachurée du triangle rectangle )
54 P(-1,2 ≤ X≤ +1,2)
A : 0,5
B : 0,6
C : 0,3
D : 0,9
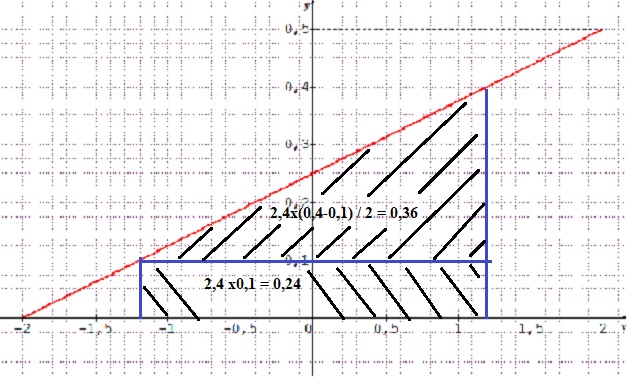
|
|
|
|
|
55. On A :
A : E(X) = 0
B : -2 ≤ E(X) < 0
C : 0 < E(X) ≤ 1,4
D : 1,4 ≤ E(X) ≤ 2
Loi Normale
Pour les questions 56 et 57 on considère une variable aléatoire Y = 2X
une variable aléatoire qui suit une loi normale centrée réduite.
56 : La variable Y
A : est plus dispersée que X.
B : est moins dispersée que X.
C : a la même dispersion que X.
D : on manque d’informations pour comparer les dispersions de X et Y.
57 : Le graphique ci-dessous représente la densité d’une loi normale centrée réduite.

alors la densité de Y est :
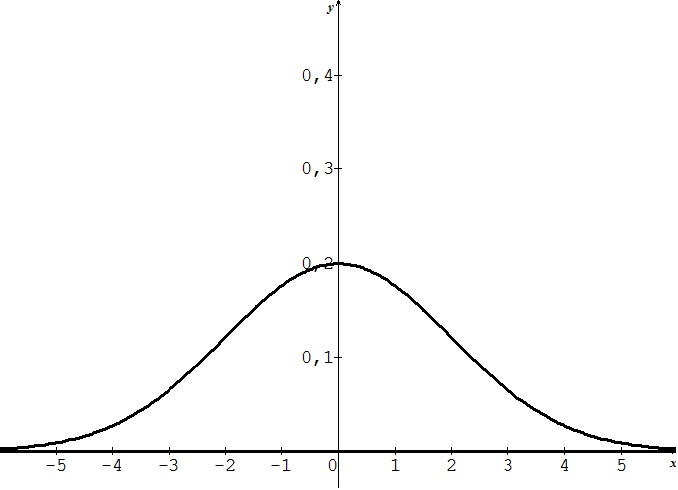 réponse B réponse B
La loi de Y reste centrée et la courbe est plus étalée, Y est plus dispersée que X.
Pour
les questions 58 et 59 on considère une variable aléatoire Z qui suit
une loi normale d’espérance 3 et d’écart type 2, on peut utiliser le
tableau suivant :
k
|
0,25
|
0,5
|
0,75
|
1
|
1,25
|
p(X < k) où X suit une loi normale centrée réduite
|
0,60
|
0,69
|
0,77
|
0,84
|
0,89
|
58. P(Z ≤ 4 ) =
A : 0,84
B : 0,69
C : 0,77
D : Aucune des réponses précédentes n’est exacte.
On pose Y = (Z-3) / 2 =0,5 Z -1,5 ; Y suit la loi normale centrée réduite.
P(Z < 4 ) = P(Y < (4-3) / 2 ) = P (Y < 0,5 ) =0,39
|
|
59. P(2 < Z ≤ 5 ) =
A : 0,14
B : 0,29
C : 0,77
D : 0,53.
On pose Y = (Z-3) / 2 =0,5 Z -1,5 ; Y suit la loi normale centrée réduite.
P(2 < Z ≤ 5 ) = P( (2-3) / 2 <Y < (5-3) / 2 ) = P (-0,5 <Y < 1 ) =0,84-(1-0,69) = 0,53.
Statistiques
60 : On considère
une variable aléatoire qui suit une loi binomiale B (n ; p) avec n
entier naturel différent de zéro et p appartenant à [0 ; 1 ]. On notef
= x / n la fréquence associée à X. Alors si n est assez grand on a :
A. P(f-1/n½ < p < f+1/n½ ) =0,68
B. P(f-1/n½ < p < f+1/n½ ) < 0,95
C. P(f-1/n½ < p < f+1/n½ ) > 0,95.
D : aucune des réponses précédentes n’est exacte
|
|
|
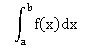 est
est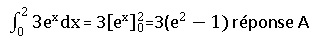
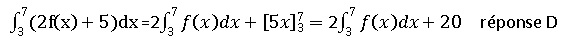
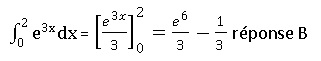




 réponse B
réponse B