Mathématiques,
concours Ecole de santé des armées ( ESA) 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Exercice 1.
QCM 1 :
Soit la fonction h définie pour out réel x par h(x) = e−x −x +4. Soit C la courbe représentative de h. :
A. h'(x) =e-x-1. Faux.
h'(x) = -e-x-1=-(e-x+1), toujours négative ; h(x) est strictement décroissante.
B. h admet un maximum.
Faux.
C. C admet une asymptote horizontale. Faux.
Au voisinage de +oo, le terme en exponentielle tend vers zéro ; h(x) tend vers -oo.
Au voisinage de -oo, le terme en exponentielle l'emporte sur -x+4 et h(x) tend vers +oo..
D. L'équation h(x) =5 a une solution unique dans l'ensemble des réels. Vrai.
h(x) strictement décroissante et h(x) décrit R.
QCM 2 :
Dans l’ensemble des nombres réels, l’inéquation −2xe−x+1 > 0 a pour ensemble de solutions :
A. aucune.
Le terme en exponentielle est positif.
-2x est positif ou nul pour x appartenant à ]-oo ; 0].
B. { 0 }
C. ]-oo ; 0 ]. Vrai.
D. [0 ; +oo[.
QCM 3 :
On considère l'intégrale I suivante.
On pourra, pour calculer I , utiliser la dérivée de la fonction h définie sur [1 ; e] par h(t ) = t3[3ln(t )−1].
La valeur exacte de I est :
Calcul de h'(x) : on pose u = t3 et v = 3 ln(t)-1 ; u' = 3t2 ; v' = 3 /t.
u'v+v'u =3t2(3ln(t)-1) +3t2=9t2ln(t).
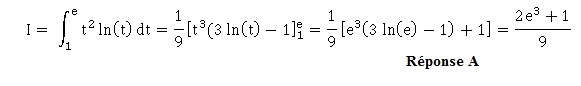
QCM
4.Soit la fonction f définie pour tout réel x par f (x) = x cos x.
La dérivée f ′ de f est définie pour tout réel x par f ′(x) = :
A. -sin(x);
B. {cos(x).
C. cos(x) +x sin(x)
D. cos (x)-x sin(x). Vrai.
On pose u = x et v = cos (x) ; u'=1 ; v' = -sin(x) ; u'v+v'u = cos(x)-x sin(x).
QCM 5 :
Soit la fonction f définie pour tout réel x par f (x) = x cos x.
La primitive F de f telle que F(0) = 1 est définie pour tout réel x par F(x)= :
A. 0,5x2 sin(x)+1.
On dérive : F'(x) = x(sin(x)+0,5x2 cos(x) différent de f(x).
B. -0,5x2 sin(x)+1.
On dérive : F'(x) = -x(sin(x)-0,5x2 cos(x) différent de f(x).
C. cos(x) + x sin(x). Vrai.
F'(x) = -sin(x) +sin(x) +xcos(x) =f(x) ; F(0) = 1.
D. cos(x) - x sin(x).
F'(x) = -sin(x) -sin(x) -xcos(x) différent de f(x).
QCM 6 :
L'intégrale suivante est égale à :
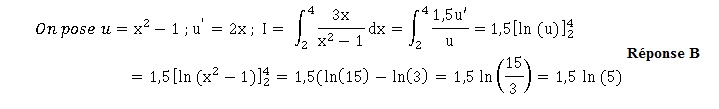 QCM 7 :
QCM 7 :
On considère la fonction f dérivable sur ]0 ;+∞[ et définie par f (x) =( −x2 −2ln(x)) / x :
La limite de f en +∞ est égale à :
A. 0
B. -oo. Vrai.
C. +oo
D. 1
f(x) = -x-ln(x) / x.
Au voisinage de +oo : -x tend vers -oo et ln(x) / x tend vers zéro.
|
| .
. |
|
|
Exercice 2
QCM 8 :
Une solution de l'équation suivante est :
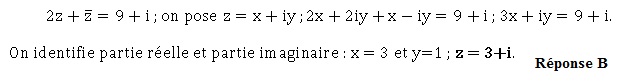
QCM 9 :
On considère la suite u définie par son premier terme u0 = 1 et la relation de récurrence : un+1 = un/ 3+2
A : la suite u est géométrique.
B : la suite u est arithmétique.
C : la suite u est majorée par 3. Vrai.
D : la suite u est convergente vers 2.
u1 = u0 / 3 +2 = 7 /3 ; u2 = u1 / 3 +2 = 25 /9 ; u3 = u2 / 3 +2 = 79 / 27 ;
Proposition un < 3.
Raisonnement par récurence : Initialisation : u0 = 1 est vrai.
Hérédité : on suppose un vrai ; un/ 3+2 <3 ; donc un+1 <3.
Conclusion : la propriété est vraie au rang zéro et héréditaire, donc un<3 quel que soit n.
QCM 10 :
On considère trois suites u, v, et w qui vérifient la propriété suivante :
Pour tout entier naturel n non nul : un < vn < wn.
Quand n tend vers plus l'infini, un tend vers 2 et wn = un + 1/n, alors :
A : on ne peut pas dire que la suite (vn) converge
B : la suite (vn) n’a pas de limite.
C. Quand n tend vers plus l'infini, vn > 2.
D. Quand n tend vers plus l'infini, vn tend vers 2. Vrai ( d'après le théorème d'encadrement par des limites).
QCM 11 :
Un sac contient 4 boules noires et 3 boules rouges.On tire successivement et sans remise 2 boules du
sac. Sachant que la première boule tirée est noire, la probabilité de la seconde soit noire est :
A. 2/7
B. 4/7
C.1/2. Vrai.
D. 2/3.
Dans
le sac, il reste 6 boules, trois noires et trois rouges : la
probabilité de tirer une boule noire est égale à 3 / 6 = 1 / 2.
QCM 12 :
On lance un dé cubique bien équilibré et on lit le numéro inscrit sur la face supérieure de dé.
Soit les évènements :
I : « le numéro est inférieur ou égal à 3 ».
M : « le numéro est un multiple de 3 ».
A. P(I u M) = 5 /6
B. P(I n M) =0,5
C. I et M sont incompatibles.
D. I et M sont indépendants. Vrai.
P(I) ={1 ; 2 ; 3} =3/6 = 0,5 ; P(M) ={3 ; 6 }= 2 / 6 = 1 /3.
P(I n M) ={ 3}= 1 / 6 = P(I) x P(M) donc I et M sont indépendants.
P(I u M) ={1 ; 2 ; 3 ; 6 }=4 / 6 = 2 /3.
QCM
13 :
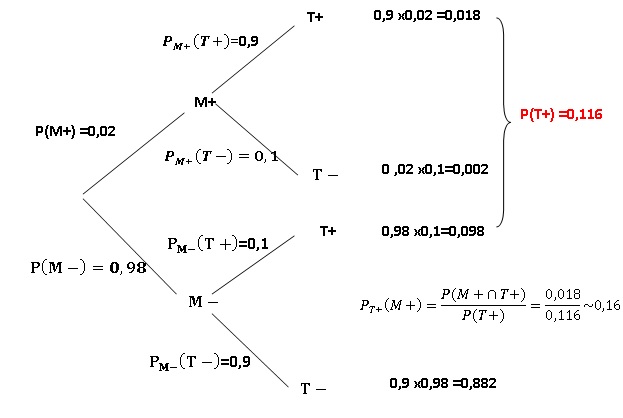
Une maladie frappe 2% de la population d’un pays. Pour dépister cette maladie, on utilise un test. On sait que :
- la probabilité que le test soit positif, sachant que l’individu est malade, est 0,9 ;
- la probabilité que le test soit négatif, sachant que l’individu n’est pas malade, est 0,9.
On note les évènements :
M+ : « l’individu est malade »
M− : « l’individu n’est pas malade »
T+ : « le test est positif »
T− : « le test est négatif »
A. PM+(T+) = 0,1.
B. P(T+)=0,278
C. P(T+)=0,22
D. PT+(M+)=0,16. Vrai.
QCM 14 :
X est une variable aléatoire suivant une loi uniforme sur [2 ; 20].
La probabilité PX>6(5 < X < 10) est égale à :
A. 5 / 18
B. 5 / 14
C. 2 / 7. Vrai.
D. 1 /4
P(X>6) =(20-6) / 20-2) = 14 / 18 = 7 / 9 ;
P(X>6) n P(5 < X < 10) = (10-6) / (20-2) = 4 / 18 = 2 / 9.
[ P(X>6) n P(5 < X < 10)] / P(X>6) = 2 / 7.
|
|
|
|
Exercice
3.
Un essai thérapeutique est réalisé chez des patients atteints d’une maladie associée à une très forte mortalité. Les
données de cet essai sont correctement ajustées par un modèle de survie exponentielle.
Soit XA la variable aléatoire qui suit la loi exponentielle de paramètre lA = 0,22.
Soit XB la variable aléatoire qui suit la loi exponentielle de paramètre lB = 0,11.
t représente le temps en années.
Avec un traitement A, la probabilité de survie à l’instant t est égale à SA(t )= P(XA > t ).
Avec un traitement B, la probabilité de survie à l’instant t est égale à SB (t ) = P(XB > t ).
Aide aux calculs e−2,2 ≈ 0,111 et racine carrée (0,111) ≈ 0,333.
1. Calculer P (XA < 10).
P (XA < 10)=1-exp(-0,22 x10) = 1-exp(-2,2) ~1-0,111 = 0,889.
2. Démontrer que pour tout réel t positif, SA(t ) = exp(−0,22t).
P(XA > t ) +P(XA < t ) = 1 ;
P(XA < t ) =1-exp(-0,22 t) ;
P(XA > t )1-(1-exp(-0,22 t)) = exp(-0,22t).
3. Donner le tableau de variation complet de la fonction SA. Justifier.
S'A(t) = -0,22 exp(-0,22t).
Le terme en exponentielle est positif ; S'A(t) est négative sur [0 ; +oo[.
SA(t ) est strictement décroissante sur [0 ; +oo[.
SA(0 ) =1 ; quand t tend vers l'infini, SA(t ) tend vers zéro.
4. Calculer la probabilité de survie à 10 ans dans le cas du traitement B.
SB (t )=1-exp(-0,11 x10) = 1-exp(-1,1) ~1-0,111½ =1-0,333 ~ 0,667.
5. Calculer la probabilité de survie à 5 ans dans le cas du traitement A.
SA(5 )=exp(-0,22 x5) = exp(-1,1) =0,111½ = 0,333.
6. Le rapport de survie des traitements A et B est-il constant au cours du temps ?
7. Pour t fixé, établir la relation entre la survie dans le cas du traitement A et la survie dans le cas du traitement B.
SA(t ) /SB(t ) =exp(-0,22t) / exp(-0,11 t) = exp(-(0,22 -0,11)t) = exp(-0,11t).
Ce rapport n'est pas constant au cours du temps.
|
|