Mathématiques, équations différentielles, concours ingénieur
territorial.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Résolution
d'une équation différentielle. (sujet 2011)
L’étude d’un phénomène d’amortissement conduit à la résolution de
l’équation différentielle :
(E) : y"+2y' + 2y=0
où y est une fonction de la variable x, définie et deux fois dérivable
sur ℝ.
Résoudre
(E) sur R.
Equation caractéristique : r2+2r+2=0 avec a=1,
b=2, c=2.
Discriminant D
= b2-4ac =4-4*2=-4 = 4 i2
avec i2 = -1.
Solutions r1 =(-b+D½)
/ (2a) =½(-2+2i) = -1 +i ; r2 =(-b-D½)
/ (2a) =½(-2-2i) = -1 -i.
Solution générale de
(E) : on pose a
=-b/(2a) =-1 et w
=(4ac-b2)½ = 2.
y = eax[(A+B)
cos wx +
i(A-B) sin wx]
= e-x[(A+B) cos 2x +
i(A-B) sin 2x].
On ne retient que les solutions réelles, A et B doivent être conjugués.
A =½(C-iD) et B =½(C+iD), C et D réels arbitraires.
Par suite : y = e-x[ C cos 2x +D sin 2x]
On pose sin f =C
/ (C2+D2)½
; cos f =
D / (C2+D2)½
;
y = A' e-xsin (2x-f), avec A' et f réels
arbitraires.
Il s'agit d'un phénomène oscillatoire amorti, l'amplitude varie en
fonction de x.
Déterminer
la solution y de (E) satisfaisant aux conditions initiales : y(0)=0 et
y'(0) =1.
y(0)=A' e0 sin (-f)=0 ;
A' sin f
=0.
A' = 0 n' a aucun intérêt en physique ; f = 0 ou p.
On pose u = A' e-x et v = sin (2x-f) ; u' = -A' e-x et v' =
2cos(2x-f).
Dérivée d'un produit : u'v+v'u = y' = -A' e-x sin (2x-f) +2A' e-xcos(2x-f).
y'0) =-A' sin(-f)
+2A' cos(-f)
= 1 ; 2A' cos(-f) = 1. A' = ½,
une amplitude est toujours positive.
y = ½ e-xsin (2x).
Sujet 2006.
Sur [0, +oo [, on donne l'équation différentielle (E) : xy' +2y = x / (1+x2).
Déterminer les solutions de (E0) : xy'+2y=0 ;
Séparer les variables : xdy/dx =-2y ; -½dy/ y = dx / x.
Intégrer : -½ln y = ln x + A ( A est une constante ).
½ln y + ln x = Cste ; ln y½ +ln x = Cste ; y½x = Cste ; y½= B/x ; y = C /x2.
Vérifier que y = (x-arctan x) / x2 est une solution particulière de (E) :
Dérivée de arctan x : 1/(1+x2).
On pose u = x-arctan x et v = x2 ; u' = 1-1/(1+x2) et v' = 2x.
Dérivée d'un quotient : y' =( u'v-v'u)/v2 = [(1-1/(1+x2))x2-2x(x-arctan x)] / x4.
y' = [x4/(1+x2)-2x2+2x arctan x]/x4 =1/(1+x2) +(-2x+2 arctan x)/x3 ;
xy' = x/(1+x2) +(-2x+2 arctan x)/x2 ;
xy'+2y = x/(1+x2) +(-2x+2 arctan x)/x2 +(2x-2arctan x)/x2 = x/(1+x2).
En déduire les solutions de (E).
solution générale de (E)= solution générale de (E0) + solution particulière de (E) :
y =(x-arctan x) / x2 +C/x2.
Déterminer la solution de (E) vérifiant y(1) = 1-0,25 p.
y(1) = 1-arctan (1)+C = 1-0,25 p ; 1-0,25 p +C = 1-0,25 p.
C = 0. y =(x-arctan x) / x2.
|
|
|
.
|
.
|
|
Sujet
2003.
Sur [0, +oo [, on donne l'équation différentielle (E) : xy' -y = x2 / (1+x).
Déterminer les solutions de (E0) : xy'-y=0 ;
Séparer les variables : xdy/dx =y ; dy/ y = dx / x.
Intégrer : ln y = ln x + A ( A est une constante ).
ln y-ln x = A ; ln(y/x) = A ; y/x = cste ; y = B x avex B une constante réelle.
Vérifier que y = x ln(1+x) est une solution particulière de (E) :
On pose u = x et v = ln(1+x) ; u' = 1 et v' = 1/(1+x).
Dérivée d'un produit y' = u'v+v'u =ln(1+x) +x/(1+x).
Repport dans (E) : xln(1+x) +x2/(1+x)-xln(1+x) = x2 / (1+x), est vérifiée quel que soit x.
y = x ln(1+x) est bien une solution de (E).
En déduire les solutions de (E).
Solution générale de (E)= solution générale de (E0) + solution particulière de (E) :
y = Bx + x ln(1+x).
|
Calcul
intégral. ( sujet 2008)
Soient f et g les fonctions définies sur R par : f(x) = x cos x et g(x)
= x sin x.
Calculer
la primitive F de la fonction f qui vérifie F(0) =1.
Intégration par parties en posant u= x et v' = cos x ; u' = 1 et v =
sin x.
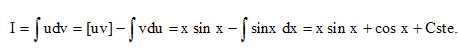
F(0) = 1+Cste = 1, la constante d'intégration est nulle et F= x sin x+
cos x.
Calculer
la primitive G de la fonction g qui vérifie G(0) =0.
Intégration
par parties en posant u= x et v' = sin x ; u' = 1 et v = -cos x.
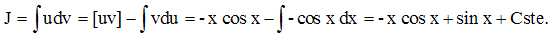
G(0) =cste = 0, la constante d'intégration est
nulle et G= -x cos x+ sin x.
Equations
différentielles. ( sujet 2008)
Résoudre
l'équation différentielle (E0) :
y"-2y'+y=0
Equation caractristique r2-2r+ 1= 0 ; (r-1)2=0,
solution unique r =1.
Solution générale de (E0) : y =(A+Bx) ex,
A et B constantes réelles.
Résoudre
l'équation différentielle (E1) :
y"-2y'+y=x2.
On cherche une solution particulière de (E1)
sous la forme : y=ax2+bx+c.
y' = 2ax+b ; y" = 2a ; repport dans (E1) :
2a-4ax-2b +ax2+bx
+c= x2 soit ax2+(b-4a)x+2a-2b+c=x2.
On identifie a=1 ; b = 4a = 4 et c=6.
y = x2+4x+6 est une solution particulière de (E1).
La solution générale de (E1) est obtenue en
faisant la somme de la solution générale de (E0)
et d'une solution particulière de (E1).
y = (A+Bx)
ex + x2+4x+6.
Résoudre
l'équation différentielle (E2) :
y"-2y'+y =x ex sin x.
On pourra introduire la fonction z = y e-x et
rechercher une solution particulière de (E2).
z' = y' e-x -ye-x ; z" =
y"e-x
- y' e-x
-y'e-x
+ye-x =e-x(y"-2y' +y),
soit : y"-2y'
+y = z" ex.
Par suite : z" ex =x ex sin
x ; z" = x sin x.
z' = G=
-x cos x+ sin x+ C ( C est une constante)
z = -F-cos
x +Cx+D=-( x sin x + cos x)-cos x +Cx+D.
y = z ex = [-( x sin x +2 cos x) +Cx+D]ex.
Solution générale de (E2) = solution générale de
(E0) + solution particulière de (E2).
y =(A+Bx) ex
+ [-( x sin x + 2cos x) +Cx+D]ex.
Résoudre
l'équation différentielle (E) : y"-2y'+y =x2+x
ex sin x.
Solution particulière de (E) = solution particulière de (E1)+solution
particulière de (E2).
Solution
générale de (E) = solution générale de (E0) +
solution particulière de (E).
|
.
|