Mathématiques,
Matrices, chiffrement, Bac S 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Pondichéry.
Partie A.
Données :

On considère les matrices M de la forme M où a et b sont des nombres
entiers.
Le nombre 3a −5b est appelé le déterminant de M. On le note det(M).
Ainsi det(M) = 3a −5b.
1. Dans cette
question on suppose que det(M) diffère de zéro. Justifier que N est
l’inverse de M.
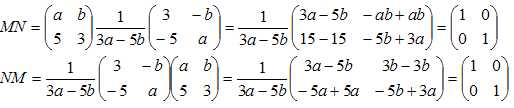
La matrice N est donc l'inverse de la matrice M.
2. On considère
l’équation (E) : det(M) = 3.
On souhaite déterminer tous les couples d’entiers (a ; b) solutions de
l’équation (E).
a. Vérifier que le
couple (6 ; 3) est une solution de (E).
3a-5b = 3*6-5*3 = 3
b. Montrer que le
couple d’entiers (a ; b) est solution de (E) si et seulement si 3(a −6)
= 5(b −3).
En déduire l’ensemble des solutions de l’équation (E).
Hypothèse
: le couple (a,b) est solution de E : 3a-5b=3
Le couple (6 ; 3 ) est solution de (E) :3*6-5*3 = 3
Soustraire : 3(a-6) -5(b-3) =0 soit 3(a −6) = 5(b −3).
Réciproque :
si ( a ; b ) vérifie 3(a-6)=5(b-3) alors :
3a-18 = 5 b-15 soit 3a-5b = 3 , par suite le couple (a ; b) est
solution de (E).
En conséquence lecouple (a ; b) est solutionde (E) si et seulement si
3(a-6) = 5(b-3).
Solutions de (E).
3
et 5 sont premiers entre eux : si 3(a-6) = 5(b-3) alors (b-3) est un
multiple de trois ; b-3 s'écrit : b-3 = 3 k soit b = 3k+3 avec k
entier relatif. Par suite : a-6 = 5 k. soit a = 5 k+6.
Les solutions de (E) sont l'ensemble {(6+5k) ; (3+3k)} avec k entier
relatif.
Partie B.
1. En
utilisant la partie A, déterminer la matrice inverse de Q.
Le déterminant de Q est det(Q) =6*3 -3*5 = 3.
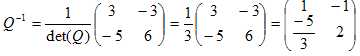
2. Codage avec la
matrice Q
Pour coder un mot de deux lettres à l’aide de la matrice Q on
utilise la procédure ci-après :
Étape 1 :
On associe au mot la matrice X où x1 est l’entier
correspondant à la première lettre du mot et x2 l’entier
correspondant à la deuxième lettre du mot selon le tableau de
correspondance.
Étape 2 :
La matrice X est transformée en la matrice Y¶telle que Y = QX
Etape 3 :
La matrice Y est transformée en la matrice R telle que r1
est le reste de la division euclidienne de y1 par 26 et r2
est le reste de la division euclidienne de y2 par 26.
Étape 4 :
À la matrice R on associe un mot de deux lettres selon le tableau de
correspondance.
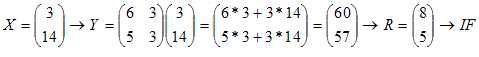
3. Procédure de
décodage.
On conserve les mêmes notations que pour le codage.
Lors du codage, la matrice X a été transformée en la matrice Y telle
que Y =QX.
Décoder
le mot SG.
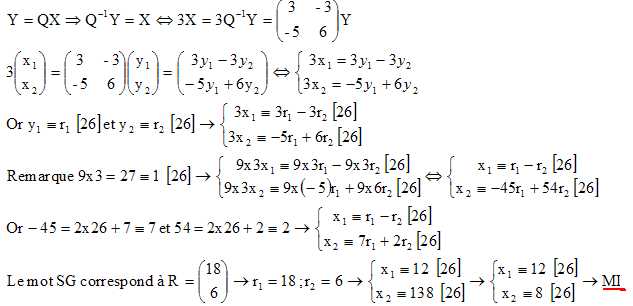
|
| .
. |
|
|
Amérique du Nord.
On dispose de deux urnes U et V contenant chacune
deux boules.
Au départ, l’urne U contient deux boules blanches et l’urne V contient
deux boules noires. On effectue des tirages successifs dans ces urnes
de la façon suivante : chaque tirage consiste à prendre au hasard, de
manière simultanée, une boule dans chaque urne et à la mettre dans
l’autre urne.
Pour tout entier naturel n non nul, on note Xn la variable
aléatoire égale au nombre de boules blanches que contient l’urne U à la
fin du n-ième tirage.
1. a. Traduire par
une phrase la probabilité P(Xn=1) (Xn+1 = 1) puis
déterminer les probabilités conditionnelles suivantes :
P(Xn=0) (Xn+1 = 1) ,P(Xn=1) (Xn+1
= 1) et P(Xn=2) (Xn+1 = 1) .
P(Xn=1)
(Xn+1
= 1) est la probabilité qu'il y ait exactement une boule blanche dans
l'urne U après le n+1 -ième tirage sachant qu'il y en avait
exactement une au n-ième tirage.
La sitution est
inchangée si on tire une boule blanche dans chaque urne ( probabilité
0,25) ou bien si on tire une boule noire dans chaque urne ( probabilité
0,25). P(Xn=1) (Xn+1 = 1) est égale à 0,5.
P(Xn=0)
(Xn+1 = 1) =1, l'urne U ne contient que
des boules noires et l'urne V ne contient que des boules blanches.
P(Xn=2)
(Xn+1 = 1), l'urne U ne contient que des boules
blanches et l'urne V ne contient que des boules noires.
b.
Exprimer P (Xn+1 = 1) en fonction de P (Xn = 0) ,
P (Xn = 1) et P (Xn = 2).
Au début du (n+1)-ième tirage, (Xn
= 0), (Xn = 1) et P (Xn = 2) forment une partition
de l'univers.
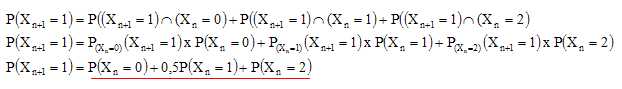
2. Pour tout entier
naturel n non nul, on note Rn la matrice ligne définie par :
Rn =(P (Xn = 0) P (Xn = 1) P (Xn =
2)) et on considère M la matrice définie ci-dessous.
On note R0 lamatrice ligne (0 0 1).
On admettra par la suite que, pour tout entier naturel n, Rn+1
= Rn ×M.
Déterminer R1 et justifier que, pour tout entier naturel n, Rn
= R0 ×Mn.
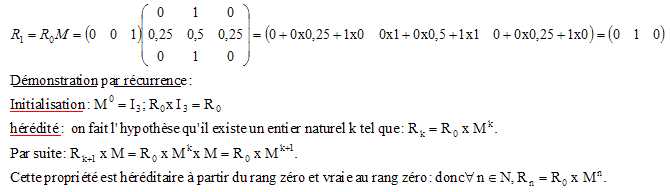
3. On admet que M
= P ×D ×P−1 définies ci-dessous.
Établir que, pour tout entier naturel n, Mn = P ×Dn
×P−1.
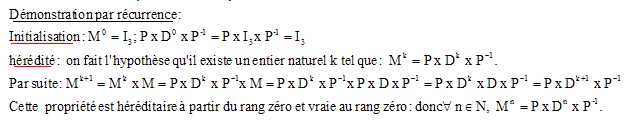
4.a.Calculer Dn
×P−1 en fonction de n.
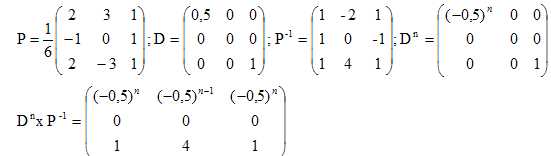
4.b. On donne R0P,
déterminer les coefficients de Rn en fonction de n.
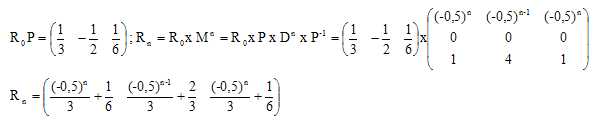
5. Déterminer les
limites suivantes et interpréter les résultats.
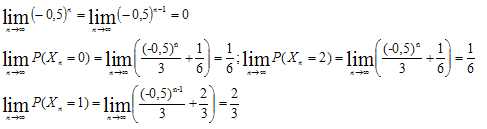
La probabilité que les urnes se retrouvent dans la position
initiale tend vers 1 /6.
La probabilité que chaque urne contienne une boule noire et une boule
blanche tend vers 2/3.
|
|
|
|
Centres
Etrangers.
Le but de cet exercice est d’étudier, sur un exemple, une méthode de
chiffrement publiée en 1929 par le mathématicien et cryptologue Lester
Hill. Ce chiffrement repose sur la donnée d’une matrice A, connue
uniquement de l’émetteur et du destinataire.
Partie A –
Chiffrement de Hill
Voici les différentes étapes de chiffrement pour un mot comportant un
nombre pair de lettres :
Étape 1 On
divise le mot en blocs de deux lettres consécutives puis, pour chaque
bloc, on effectue chacune des étapes suivantes.
Étape 2 On
associe aux deux lettres du bloc les deux entiers x1 et x2
tous deux compris entre 0 et 25, qui correspondent aux deux lettres dans
le même ordre, dans le tableau suivant :
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
M
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
N
|
O
|
P
|
Q
|
R
|
S
|
T
|
U
|
V
|
W
|
X
|
Y
|
Z
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
Étape 3 On
transforme la matrice X en la matrice Y vérifiant Y =AX.
Étape 4 On
transforme la matrice Y en la matrice R où r1 est le reste
de la division euclidienne de y1 par 26 et r2
celui de la division
euclidienne de y2 par 26.
Étape 5 On
associe aux entiers r1 et r2 les deux lettres
correspondantes du tableau de l’étape 2.
Le bloc chiffré est le bloc obtenu en juxtaposant ces deux lettres.
Question : utiliser
la méthode de chiffrement exposée pour chiffrer le mot «HILL ».
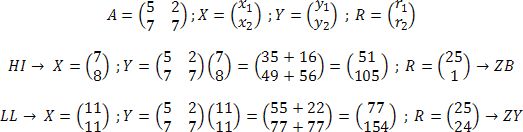
Le mot "HILL" est chiffré par le mot "ZBZY".
Partie B - Quelques
outils mathématiques nécessaires au déchiffrement.
1. Soit a un entier
relatif premier avec 26.
Démontrer qu’il existe un entier relatif u tel que u x a ≡ 1 modulo 26.
a et 26 étant premiers entre eux, il existe deux entiers u et v tels
que : au +26 v = 1 ( th. de Bézout ).
26 ≡ 0 modulo 26, alors 26 v≡ 0 modulo 26.
Ajouter "au" à chaque membre de cette congruence : 26 v+au≡ au
modulo 26 soit au ≡ 1 modulo 26.
2. On considère
l’algorithme suivant :
VARIABLES : a,u, et r sont des nombres (a est naturel et premier avec
26)
TRAITEMENT : Lire a
u prend la valeur 0, et r prend la valeur 0
Tant que r différent de 1
u prend la valeur u +1
r prend la valeur du reste de la division euclidienne de u x a par 26
Fin du Tant que
SORTIE Afficher u
On entre la valeur a = 21 dans cet algorithme.
a. Reproduire sur
la copie et compléter le tableau suivant, jusqu’à l’arrêt de
l’algorithme.
u
|
0
|
1
|
2
|
3
|
4
|
5
|
r
|
0
|
21
|
16
|
11
|
6
|
1
|
L'algorithme affiche 5, c'est à dire 21 x 5 ≡ 1 modulo 26.
3. a. Calculer la matrice 12A− A2.
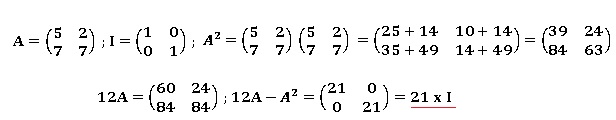
b. En déduire la
matrice B telle que B A = 21I .
12A-A2 = 12 A I -A2 = A ( 12 I-A) = 21 I ; par
suite B = 12 I-A.
c. Démontrer que si
AX = Y , alors 21X = BY .
On suppose que : A x X = Y.
Multiplions à gauche, chaque membre par B : B x A x X = B x Y.
21 I x X = B x Y soit 21X = BY.
Partie C -
Déchiffrement
On veut déchiffrer le mot VLUP.
On note X la matrice associée, selon le tableau de correspondance, à un
bloc de deux lettres avant chiffrement, et Y
la matrice définie par l’égalité : Y =AX.
1. Démontrer que :
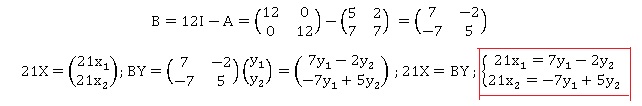
2. En utilisant la
question B .2., établir que :
Soit r1 et r2 sont les restes respectifs de y1
et y2 dans la division euclidienne par 26
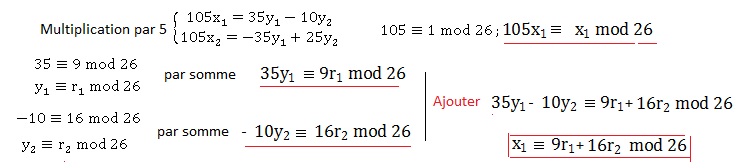

3. Déchiffrer le
mot VLUP.
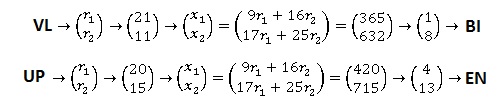
|
|
Asie.
Partie B : Méthode de cryptage
(pour un mot comportant un nombre pair de lettres)
Exemple : avec le mot ESPION
1. On regroupe les lettres par paires. ES PI ON
2. On remplace les lettres par les valeurs associées à l’aide du
tableau précédent, et on place les couples de nombres obtenus dans des
matrices colonne.
3. On multiplie les matrices colonne par la gauche par la matrice A
4. On remplace chaque coefficient des matrices colonne obtenues par
leur reste dans la division euclidienne par 26.
5. On utilise le tableau de correspondance entre lettres et nombres
pour obtenir le mot crypté.
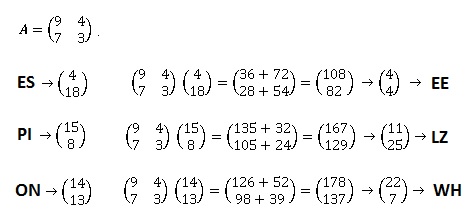
Méthode
de décryptage
Soient a, b, x, y,
x′ et y′ des nombres entiers relatifs.
On sait que si x ≡ x′ modulo 26 et y ≡ y′ modulo 26 alors : ax +by ≡
ax′ +by′ modulo 26.
Ce résultat permet d’écrire que, si A est un ematrice 2×2, et B et C
sont deux matrices colonne 2×1, alors :
B ≡C modulo 26 implique AB ≡ AC modulo 26.
a. Établir que la
matrice A est inversible, et déterminer son inverse.
b. Décrypter le
mot : XQGY.
Pour décrypter les lettres XQ, on cherche la matrice colonne
correspondant à ces deux lettres puis on multiplie à gauche par la
matrice A−1.
On fait de même pour les lettres GY.
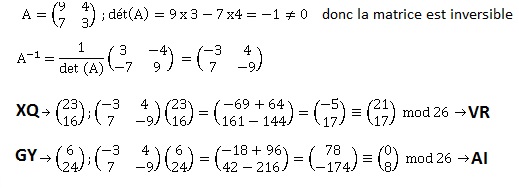
Antilles.
Le plan complexe est rapporté à un repère orthonormé
On considère la droite D d’équation 7x −3y −1 = 0
On définie la suite (An) de points du plan de coordonnées (xn
: yn) vérifiant pour tout n entier naturel :
x0 = 1; y0 = 2 et xn+1 = −6,5 xn
+3yn : yn+1 = −17,5 xn +8yn.
1. On note M
et Xn les matrices suivantes.
a. Montrer que,
pour tout entier naturel n, Xn+1 =MXn.
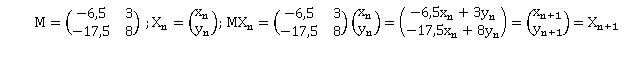
b. Sans justifier,
exprimer pour tout entier naturel n, Xn en fonction de Mn
et X0.
La suite Xn est géométrique de raison M et de premier terme X0.
Xn = Mn X0.
2. On considère la
matrice P et on admet que la matrice inverse de P, notée P−1,
est définie par P−1.
a. Vérifier que P−1MP
est une matrice diagonale D que l’on précisera.
b. Pour tout entier
naturel n, donner Dn sans justification.
c. Démontrer par
récurrence que, pour tout entier naturel n,Mn = PDnP−1.

3. On admet que,
pour tout entier naturel n, l'expression suivante de Mn.
En déduire que, pour tout entier naturel n, une expression de xn
et yn en fonction de n.
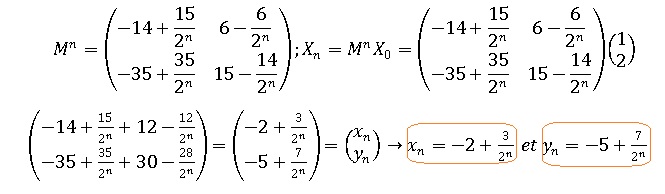
4. Montrer que,
pour tout entier naturel n, le point An appartient à la
droite D.
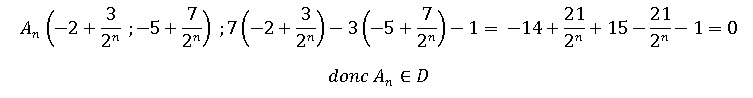
|
|