Mathématiques, loi
normale, loi exponentielle, bac S 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Amérique
du Nord
Partie A.
Dans le cadre de son activité, une entreprise reçoit régulièrement des
demandes de devis. Les
montants de ces devis sont calculés par son secrétariat. Une étude
statistique sur l’année écoulée
conduit à modéliser le montant des devis par une variable aléatoire X
qui suit la loi normale d’espérance µ= 2900 euros et d’écart-type
s=
1250 euros.
1. Si on choisit au
hasard une demande de devis reçue par l’entreprise, quelle est la
probabilité
que le montant du devis soit supérieur à 4000 euros ?
p(X > 4000) =1-P(X
<
4000)=1-0,81057 ~0,189.
2. Afin d’améliorer
la rentabilité de son activité, l’entrepreneur décide de ne pas donner
suite à
10% des demandes. Il écarte celles dont le montant de devis est le
moins élevé. Quel doit être
le montant minimum d’un devis demandé pour que celui-ci soit pris en
compte ? Donner ce
montant à l’euro près.
On recherche x tel que P(X < x) = 0,1.
Utiliser la touche " inverse loi normale" de la calculatrice : x = 1298 €.
Partie B.
Ce même entrepreneur décide d’installer un logiciel anti-spam. Ce
logiciel détecte les messages
indésirables appelés spams (messages malveillants, publicités, etc.) et
les déplace dans un fichier
appelé "dossier spam". Le fabricant affirme que 95 % des spams sont
déplacés. De son côté, l’entrepreneur sait que 60% des messages qu’il
reçoit sont des spams. Après installation du logiciel, il constate que
58,6% des messages sont déplacés dans le dossier spam.
Pour un message pris au hasard, on considère les événements suivants :
• D : « le message est déplacé » ;
• S : « le message est un spam».
1. Calculer P(S n
D).
0,60 x0,95 = 0,57.
2. On choisit au
hasard un message qui n’est pas un spam. Montrer que la probabilité
qu’il soit
déplacé est égale à 0,04.
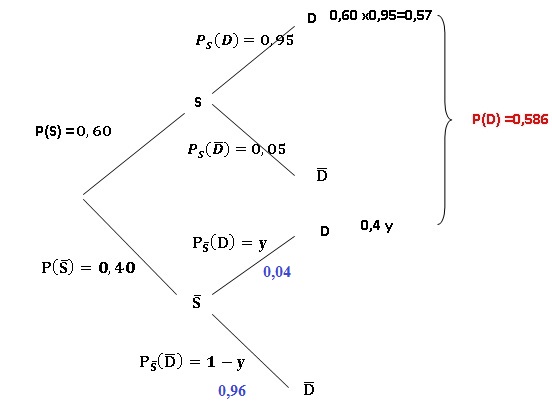
0,586 = 0,57 +0,4 y ; y = (0,586-0,57) / 0,4 = 0,04.
3. On choisit au
hasard un message non déplacé. Quelle est la probabilité que ce message
soit
un spam ?
Probabilité qu'un message soit non déplacé :
0,96 x0,40 + 0,60 x0,05 = 0,414.
Probabilité
qu'un message non déplacé soit un spam : 0,05 x0,60 /0,414=0,072.
4. Pour le logiciel
choisi par l’entreprise, le fabricant estime que 2,7 % des messages
déplacés
vers le dossier spam sont des messages fiables. Afin de tester
l’efficacité du logiciel, le secrétariat
prend la peine de compter le nombre de messages fiables parmi les
messages déplacés.
Il trouve 13 messages fiables parmi les 231 messages déplacés pendant
une semaine.
Ces résultats remettent-ils en cause l’affirmation du fabricant ?
n >0 ; np =231 x0,027 =6,237, supérieur à 5 ; nq = 231
x(1-0,027)=224,7, supérieur à 5.
Intervalle de fluctuation asymptotique au seuil de 95 %:
1,96 x(p q / n)½ = 1,96 x (0,027 (1-0,027) / 231)½=0,021.
0,027+0,021 = 0,048 ; 0,027-0,021=0,006.
Intervalle de confiance [0,006 ; 0,048 ].
13 / 231 = 0,056 ; cette valeur n'appartient pas à l'intervalle de
confiance.
L'affirmation du fabricant est remise en cause.
|
| .
. |
....
.....
|
Liban.
Dans cet exercice, on étudie quelques grandeurs
caractéristiques du fonctionnement des parkings
d’une ville. Dans tout l’exercice, les probabilités seront données avec
une précision de 10-4.
Partie A.Durée d’attente pour entrer
dans un parking souterrain.
On appelle durée d’attente le temps qui s’écoule entre le moment où la
voiture se présente à l’entrée
du parking et le moment où elle franchit la barrière d’entrée du
parking. Le tableau suivant
présente les observations faites sur une journée.
Durée
(min)
|
[0
; 2[
|
[2
; 4[
|
[4
; 6[
|
[6
; 8[
|
Nombre
de voitures
|
75
|
19
|
10
|
5
|
1. Proposer une estimation de la
durée d’attente moyenne d’une voiture à l’entrée du parking.
(75 +3 x19 +5 x10 +7 x5) / (75 +19 +10 +5) =217 /109 ~1,991 min.
2. On décide de
modéliser cette durée d’attente par une variable aléatoire T suivant
une loi exponentielle de paramètre l (exprimé en minute).
a) Justifier que
l’on peut choisir l=
0,5 min.
l=1/1,991
=109 / 217 ~0,50 min.
b) Une voiture se
présente à l’entrée du parking. Quelle est la probabilité qu’elle mette
moins de deux minutes pour franchir la barrière ?
P(T < 2)=1-
exp(-0,50 x2) =0,6321.
c) Une voiture
attend à l’entrée du parking depuis une minute.Quelle est la
probabilité qu’elle franchisse la barrière dans la minute suivante ?
La loi exponentielle est sans mémoire ; P(T < 1)=1- exp(-0,50 ) =0,3935.
Partie B - Durée et tarifs de
stationnement dans ce parking souterrain.
Une fois garée, la durée de stationnement d’une voiture est modélisée
par une variable aléatoire D qui suit la loi normale d’espérance µ= 70
min et d’écart-type s=
30 min.
1.a) Quelle est la
durée moyenne de stationnement d’une voiture ?
70 min.
b) Un automobiliste
entre et se gare dans le parking. Quelle est la probabilité que sa
durée de stationnement dépasse deux heures ?
P(D >120) = 1-P(D<120) = 1-0,9522 =0,0478.
c) À la minute
près, quel est le temps maximum de stationnement pour au moins 99 % des
voitures ?
La touche inverse loi normale de la calculatrice donne 140 min.
2. La durée de
stationnement est limitée à trois heures. Le tableau donne le tarif de
la première
heure et chaque heure supplémentaire est facturée à un tarif unique.
Toute heure commencée
est due intégralement.
Durée
|
Inférieure
à 15 min
|
Entre
15 min et 1 heure
|
heure
supplémentaire
|
Tarif
(€)
|
Gratuit
|
3,5
|
t
|
Déterminer le tarif t de
l’heure supplémentaire que doit fixer le gestionnaire du parking pour
que le prix moyen de
stationnement d’une voiture soit de 5 euros.
P(D < 15) =
0,033376.
P(15 < D < 60) =P(D <60) -P(D <15)=0,36944-0,033376=0,33606.
P(60 < D < 120) =P(D <120) -P(D <60)=0,95221-0,36944=0,5828.
P(120 < D < 180) =P(D <180) -P(D <120)=0,99988-0,95221=0,04466.
E(D) = 5 =
0,33606 x 3,5
+0,5828( 3,5+t) +0,04466(3,5 +2t).
5 =1,176 +2,040 +0,1563 +0,67212 t.
1,627 =0,67212 t ; t = 2,42 €.
Partie C.Temps
d’attente pour se garer dans un parking de centre-ville
La durée de stationnement d’une voiture dans un parking de centre-ville
est modélisée par une variable aléatoire T ' qui suit une loi normale
d’espérance µ' et d’écart-type s'.
On sait que la moyenne du temps de stationnement dans ce parking est
égale à 30 minutes et que 75% des voitures ont un temps de
stationnement inférieur à 37minutes.
Le gestionnaire du parking vise l’objectif que 95 % des voitures aient
un temps de stationnement entre 10 et 50 minutes. Cet objectif est-il
atteint ?
µ' = 30 et P(T ' < 37)
= 0,75.
On pose X = ( T '-30) / s'
=7 / s' suit la
loi normale centrée réduite.
P(X < 7
/ s')=0,75 ; 7
/ s' =0,675 ; s' = 7 /0,675 ~10,4.
P( 10 < T ' < 50) = P(T ' < 50) -P(T ' < 10) =0,945, inférieur
à 0,95..
L'objectif n'est pas atteint.
|
|
|
Centres
étrangers.
On étudie la production
d'une usine qui produit des
bonbons, conditionnés en sachets.
On choisit un sachet au hasard
dans la production journalière. La masse
de ce sachet ( en g ), est modélisée par une variable aléatoire X qui
suit une loi normale d'espérance µ = 175. Une observation statistique a
montré que 2 % des sachets ont une masse inférieure ou égale à
170 g, ce qui se traduit par : P(X <170) = 0,02.
1. Quelle est la probabilité,
arrondie au centième, de l'événement " la masse d'un sachet est
comprise entre 170 et 180 g" ? 0,04 , 0,96 ; 0,98 ; on ne peut pas
répondre car il manque des données.
On pose Y = (X-175) / s
= -5 /s
avec s
l'écart type.
Y suit la loi normale centrée
réduite ; P( Y < -5 /s)=0,02.
On utilise la touche " inverse
loi normale" de la calculatrice pour
trouver : -5 /s
=
-2,054.
Par suite s = 5 /
2,054 ~2,434.
P(170< X < 180 ) =P(-2,054 < Y < 2,054) =1-0,02-0,02 = 0,96. Réponse b.
Les différents bonbons sont
enrobés d'une cire commestible. Ce procédé,
qui déforme certains bonbons, est effectué par deux machines A et B.
Lorsqu'il est produit par A, la probabilité qu'un bonbon prélevé
aléatoirement soit déformé est égale à 0,05.
2. Sur un
échantillon aléatoire de 50 bonbons issus de A, quelle est la
probabilité, arrondie au centième, qu'au moins 2 bonbons soit déformés
? 0,72 ; 0,28 ; 0,54 ; on ne peut pas répondre car il manque des
données.
Soit Z la variable aléatoire
comptant le nombre de bonbons déformés.
n = 50 tirages aléatoires,
indépendantset identiques. deux issus
sont possibles :le bonbon est déformé p = 0,05 ; le bonbon n'est pas
déformé q = 1-p = 0,95.
La variable aléatoire Z suit
une loi binomiale de paramètre n = 50 et p
= 0,05.
Au moins deux signifie : 2 et
plus de deux.
P( Z>2) = 1-P(Z < 1) = 1-0,28 = 0,72 ; réponse a.
A produit un tiers des bonbons, B produit le reste.
Lorsqu'il est produit par B, la probabilité qu'un bonbon soit déformé
est égale à 0,02. On prélève au hasard dans la production un bonbon ;
celui-ci est déformé.
Quelle est la probabilité qu'il soit produit par B ? 0,02 ; 0,67 ; 0,44
;0,01.
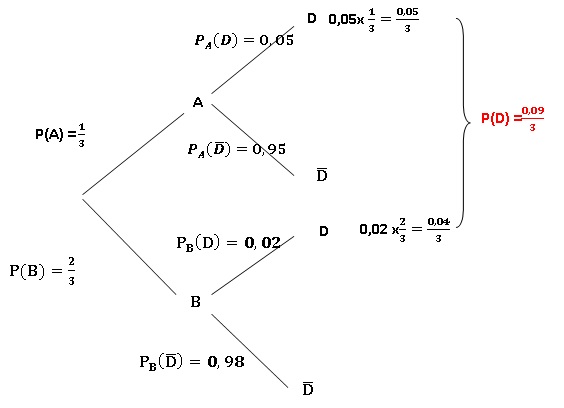
Probabilité que le bonbon
déformé soit produit par B : 0,04 / 0,09 ~0,44, réponse c.
La durée de vie de
fonctionnement ( en jours), d'une machine servant à l'emballage, est
modélisée par une variable aléatoire Y qui suit une loi exponentielle
dont l'espérance est égale à 500 jours.
4. Quelle est la
probabilité, arrondie au centième, que la durée de fonctionnement de la
machine soit inférieure ou égale à 300 jours ? 0,45 ; 1 ; 0,55 ; on ne
peut pas répondre car il manque des données.
l
= 1/500 = 0,002.
P( X < 300) =
1-exp(-0,002 x300) = 0,45, réponse a.
L'entreprise souhaite estimer la proportion de personnes de plus de 20
ans parmi ces clients, au niveau de confiance de 95 %, avec un
intervalle d'amplitude inférieure à 0,05. Elle interroge un échantillon
aléatoire de ces clients.
5. Quel est le
nombre minimal de clients à interroger ? 40 ; 400 ; 1600 ; 20.
Au seuil de 95%, intervalle de confiance (f-1/n½ ; f +1/n½].
Amplitude : 2 / n½ = 0,05 ; n½ = 2 / 0,05= 40 ; n
= 1600, réponse c.
|
|
|
|
Polynésie.
Une société fournit des
abonnements internet et des
abonnements de téléphone mobile. Un client souscrit soit un abonnement
internet, soit un abonnement téléphone mobile, il ne cumule pas les
deux. Sur la ligne d'assistance téléphonique, le client doit d'abord
signaler s'il est client internet ou s'il est client mobile. puis son
appel est mis en attente de réponse par un opérateur.
A. Durée
d'attente.
1. On s'interesse à
la durée d'attente d'un client internet lorsqu'il contact l'assistance
téléphonique avant de joindre un opérateur. Cette durée d'attente en
minute est modélisée par une varaible aléatoire D1 qui suit la
loi exponentielle de paramètre 0,6.
a. Quelle est la durée moyenne d'attente ?
1 / l = 1 /0,6 = 1,667 minutes ou 1 min 40 s.
b. Calculer la probabilité que la durée d'attente
soit inférieure à 5 minutes.
P(D1 < 5) = 1-exp(-0,6 x5) = 0,950.
2. On s'intéresse à
la durée d'attente d'un client mobile lorsqu'il contact l'assisatnce
avant de joindre un opérateur. Cette durée est modélisée par une
variable aléatoire D2 qui suit une loi exponentielle de paramètre l >0.
a. Sachant que P(D2 < 4) =0,798, déterminer l.
1-exp(-4l) = 0,798 ; exp(-4l) = 1-0,798 = 0,202.
-4l = ln(0,202) ; l
~0,4.
b. En prenant l =
0,4, peut-on considérer que moins de 10 % des clients mobiles choisis
au hasard attendent plus de 5 minutes avant de joindre un opérateur.
P(D2 > 5 ) =exp(-0,4 x5) = 0,1353 ( 13,5 %).
13,5 % des
clients mobiles choisis au hasard attendent plus de 5 minutes avant de
joindre un opérateur.
B. Obtention
d'un opérateur.
Si la durée d'attente avant
l'obtention d'un opérateur dépasse 5
minutes, l'appel prend automatiquement fin. Sinon, l'appelant obtient
un opérateur.
On choisit au hasard un client
qui appelle la ligne d'assistance. On
admet que la probabilité que l'appel émane d'un client internet est
0,7.
Si l'appel émane d'un client
internet alors la probabilité d'obtenir un opérateur est égale à 0,95.
Si l'appel
émane d'un client mobile alors la probabilité d'obtenir un opérateur
est égale à 0,87.
1. Déterminer la
probabilité qu'un client joigne un opérateur.
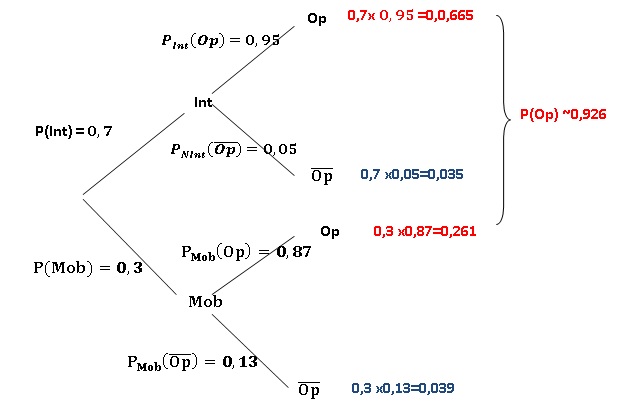
b. Un client se
plaint que son appel a pris fin au bout de 5 minutes d'attente sans
avoir obtenu d'opérateur. Est-il plus probable que se soit un client
internet ou un client mobile ?
Probabilité que l'appel prenne fin au bout de 5 minutes d'attente pour
un client :
- internet : 0,035
- mobile 0,039.
Il est probable que ce soit un client mobile.
C. Enquète de
satisfaction.
La société annonce un taux de satisfaction de 85 % pour ces clients
ayant appelé et obtenu un opérateur. Une association de consommateurs
souhaite vérifier ce taux et interroge 1303 clients. parmi celles-ci
1150 se disent satisfaites. Que pensez-vous du taux de satsifaction
annoncé par la société ?
n =1303 >30 ; p =
0,85 soit np = 1303 x0,85=1107,55 > 5.
nq = n(1-p) = 1303 x0,15 = 195,45 >5.
Au seuil de confiance de 95%, on détermine un
intervalle de fluctuation asymptotique :
1,96 (pq / n)½ = 1,96 x(0,85 x0,15 /1303)½
=0,0194.
[0,85-0,0194 ; 0,85+0,0194 ] soit [0,830 ; 0,869].
La fréquence observée est égale à 1150 /1303 ~0,883, n'appartient pas à
l'intervalle de fluctuation.
Le taux de satisfaction annoncé est trop faible, au risque de 5 %.
|
Antilles.
Dans une usine automobile, certaines pièces métalliques sont
recouvertes d’une fine couche
de nickel qui les protège contre la corrosion et l’usure. Le procédé
utilisé est un nickelage par
électrolyse.
On admet que la variable aléatoire X, qui à chaque pièce traitée
associe l’épaisseur de nickel
déposé, suit la loi normale d’espérance µ1 = 25 micromètres
(μm) et d’écart type σ1.
Une pièce est conforme si l’épaisseur de nickel déposé est comprise
entre 22,8 μm et 27,2 μm.
La fonction de densité de probabilité de X est représentée ci-dessous.
On a pu déterminer que P(X >27,2) = 0,023.
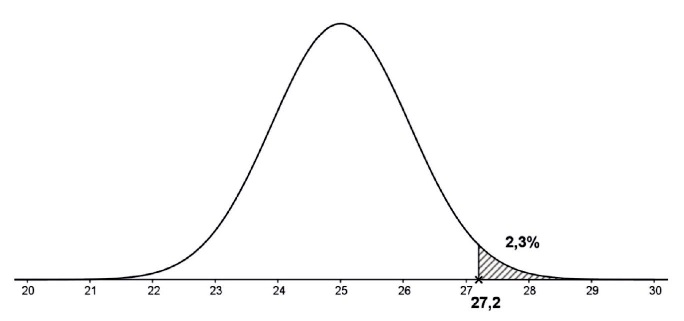
1. a. Déterminer la
probabilité qu’une pièce soit conforme.
P(22,8 < X < 27,2) = 1-0,023-0,023 =0,954.
b. Justifier que
1,1 est une valeur approchée de s1
à 10−1 près.
Le cours indique que lorsque X suit la loi normale d'espérance µ et
d'écart type s,
P(µ-2s1 < X < µ+2s1)=0,954.
22,8 = µ-2,2 ; 27,2 =µ+2,2.
2s1 =
2,2 ; s1 =
1,1.
c. Sachant qu’une pièce est
conforme, calculer la probabilité que l’épaisseur de
nickel déposé sur celle-ci soit inférieure à 24 μm. Arrondir à 10−3.
P(22,8 < X < 27,2)(X
<24)=[ P(X <24)
n ( 22,8 < X <27,1)] / P( 22,8 < X <27,1).
P(22,8 < X < 27,2)(X <24)= P(
22,8 < X < 24) / P(
22,8 < X <27,1).
P(22,8
< X < 27,2)(X
<24)=0,1589 / 0,954 = 0,167.
2.
Une équipe d’ingénieurs propose un autre procédé de nickelage, obtenu
par réaction chimique sans aucune source de courant. L’équipe affirme
que ce nouveau procédé permet théoriquement d’obtenir 98 % de pièces
conformes.
La variable aléatoire Y qui, à chaque pièce traitée avec ce nouveau
procédé, associe
l’épaisseur de nickel déposé suit la loi normale d’espérance µ2
= 25 μm et d’écart-type s2.
a. En admettant
l’affirmation ci-dessus, comparer s1 et s2.
L'espérance mathématique est identique ; Dans le second procédé, la
probabilité qu'une pièce soit conforme est 0,98, supérieure à celle du
premier procédé.
Donc s2
<s1.
b. Un contrôle
qualité évalue le nouveau procédé ; il révèle que sur 500 pièces
testées, 15 ne sont pas conformes. Au seuil de 95 %, peut-on rejeter
l’affirmation de l’équipe d’ingénieurs ?
n =500 > 30 ; p = 0,98 soit np
= 500 x0,98 = 490 >
5 ; q = 1-p = 0,02 soit nq = 500 x0,02 = 10 > 5.
Les conditions sont respectées pour définir un intervalle de
fluctuation asymptotique au seuil de 95 %.
1,96 x(pq / n)½ =1,96 x(0,98 x0,02 / 500)½ =
0,0123.
Intervalle de fluctuation : [0,98 -0,0123 ; 0,98 +0,0123 ] soit [0,968
; 0,992].
485 pièces sont conformes sur 500 ; la fréquence observées est :
485 / 500 = 0,97.
Cette valeur appartient à l'intervalle de fluctuation.
Au seuil de 95 %, on ne peut pas rejeter l'affirmation des ingénieurs.
Métropole.
On étudie un modèle de propagation d’un
virus dans une population,
semaine après semaine.
Chaque individu de la population peut être, à l’exclusion de toute
autre possibilité :
• soit susceptible d’être atteint par le virus, on dira qu’il est « de
type S » ;
• soit malade (atteint par le virus) ;
• soit immunisé (ne peut plus être atteint par le virus).
Un individu est immunisé lorsqu’il a été vacciné, ou lorsqu’il a guéri
après avoir été atteint par le virus.
Pour tout entier naturel n, le modèle de propagation du virus est
défini par les règles suivantes :
• Parmi les individus de type S en semaine n, on observe qu’en semaine
n + 1 :
85 % restent de type S, 5 % deviennent malades et 10 % deviennent
immunisés ;
• Parmi les individus malades en semaine n, on observe qu’en semaine n+
1 :
65 % restent malades, et 35 % sont guéris et deviennent immunisés.
• Tout individu immunisé en semaine n reste immunisé en semaine n + 1.
On choisit au hasard un individu dans la population. On considère les
événements suivants :
Sn : « l’individu est de type S en semaine n » ;
Mn : « l’individu est malade en semaine n » ;
In : « l’individu est immunisé en semaine n ».
En semaine 0, tous les individus sont considérés « de type S », on a
donc les probabilités suivantes :
P (S0)= 1, P(M0) = 0 et P(I0) = 0.
Partie A.
On étudie l’évolution de l’épidémie au cours des semaines 1 et 2.
1. Reproduire sur
la copie et compléter l’arbre de probabilités donné ci-dessous.
2. Montrer que P(I2)
= 0,2025.
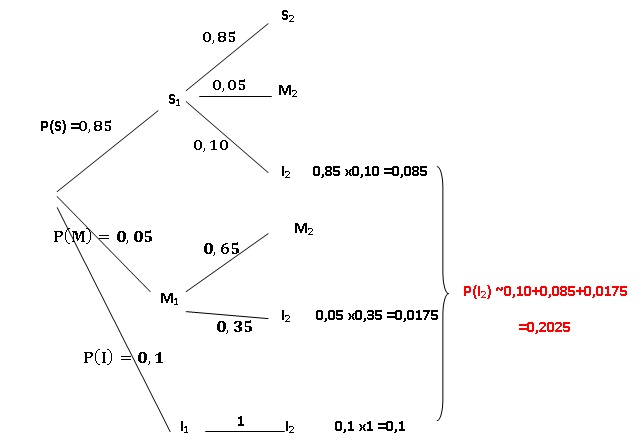
3. Sachant qu’un
individu est immunisé en semaine 2, quelle est la probabilité, arrondie
au millième, qu’il ait été malade en semaine 1 ?
PI2(M1) = P(I2 n M1) / P(I2)
= 0,05 x0,35 / 0,2025 = 7 / 81 ~0,086.
Partie B.
On étudie dans cette partie l’évolution à long terme de l’épidémie.
Pour tout entier naturel n, on note un = P(Sn) , vn
= P(Mn) et wn=P(In) les probabilités
respectives des événements Sn, Mn et In.
1. Justifier que,
pour tout entier naturel n, on a : un + vn + wn
= 1.
Chaque semaine un individu est soit de type S, soit malade , soit
immunisé..
P(Sn) +P(Mn) +P(In) = 1 ; soit un
+ vn + wn = 1.
On admet que la suite (vn) est définie par v0 = 0
et, pour tout entier naturel n :
vn+1 = 0,65vn + 0,05un.
2. À l’aide d’un
tableur, on a calculé les premiers termes des suites (un), (vn)
et (wn) :
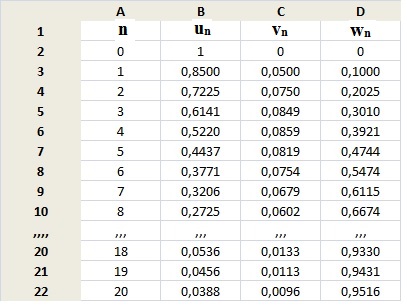
Asie.
Question
préliminaire.
Soit T une variable aléatoire suivant une loi exponentielle de
paramètre l, où l désigne un réel
strictement positif.
Démontrer que, pour tout réel a positif, P(T > a) = exp(-la).
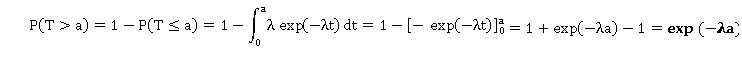
Dans la suite de l’exercice, on considère des lampes à led dont la
durée de vie, exprimée en jour, est
modélisée par une variable aléatoire T suivant la loi exponentielle de
paramètre l = 1/
2800.
Les durées seront données au jour près, et les probabilités au millième
près.
Partie A : étude
d’un exemple
1. Calculer la
probabilité qu’une lampe fonctionne au moins 180 jours.
P(T > 180) =
exp(-180 / 2800) ~0;938.
2. Sachant qu’une
telle lampe a0,938
déjà fonctionné 180 jours, quelle est la probabilité qu’elle fonctionne
encore au moins 180 jours ?
La loi exponentielle est sans mémoire, sans vieillissement..
PT > 180(
T >180+180) ~ 0,938.
Partie B : contrôle
de la durée de vie moyenne
Le fabricant de ces lampes affirme que, dans sa production, la
proportion de lampes qui ont une durée de vie supérieure à 180 heures
est de 94 %.
Un laboratoire indépendant qui doit vérifier cette affirmation fait
fonctionner un échantillon aléatoire de 400 lampes pendant 180 jours.
On suppose que les lampes tombent en panne indépendamment les unes des
autres.
Au bout de ces 180 jours, 32 de ces lampes sont en panne.
Au vu des résultats des tests, peut-on remettre en cause, au seuil de
95 %, la proportion annoncée par le fabricant ?
n = 400 > 30 ; nf = 400 x0,94 =
376 > 5 ; n(1-f) =
400 x0,06 = 24 > 5.
Les conditions sont remplies pour définir un intervalle de fluctuation.
1,96 (f(1-f) / n)½ =1,96 x(0,94 x0,06 / 400)½
=0,0233.
[0,94 -0,0233 ; 0,94 +0,0233] soit [0,917 ; 0,963].
(400-32) / 400 = 0,92.
0,92 appartient à [0,917 ; 0,963], on
ne peut pas remettre en cause la valeur annoncée par le fabricant, au
risque de 5%.
Partie C : dans une
salle de spectacle
Pour éclairer une salle de spectacle, on installe dans le plafond 500
lampes à led.
On modélise le nombre de lampes fonctionnelles après 1 an par une
variable aléatoire X qui suit la loi normale de moyenne µ = 440 et
d’écart-type s =
7,3 .
1. Calculer P ( X
> 445) , la probabilité que plus de 445 lampes soient encore
fonctionnelles après un an.
P(X >445) = 1-P(X <
445) = 1-0,753 =0,247.
2. Lors de
l’installation des lampes dans le plafond, la direction de la salle
veut constituer un stock de lampes. Quelle doit-être la taille minimale
de ce stock pour que la probabilité de pouvoir changer toutes les
lampes défectueuses, après un an, soit supérieure à 95 % ?
P (X > n) = 0,95 ; 1-P(X
< n) = 1-0,95 = 0,05.
La calculatrice donne n = 428.
On doit prévoir un stock de 500 -428 = 72 lampes.
Amérique du Sud
Sofia souhaite se rendre au
cinéma. Elle peut y aller à vélo ou en bus.
Partie A : En
utilisant le bus
On suppose dans cette partie
que Sofia utilise le bus pour se rendre au
cinéma. La durée du trajet entre son domicile et le cinéma (exprimée en
minutes) est modélisée par la variable aléatoire TB qui suit la loi
uniforme sur [12 ; 15].
1. Démontrer que la
probabilité que Sofia mette entre 12 et 14 minutes est de 2/3.
P(12 < TB < 14) =(14-12) / (15-12)
= 2 / 3.
2. Donner la durée
moyenne du trajet.
(15+12) / 2 = 13,5.
Partie B : En
utilisant son vélo
On suppose à présent que Sofia
choisit d’utiliser son vélo.
La durée du parcours (exprimée
en minutes) est modélisée par la
variable aléatoire Tv qui suit la loi normale d’espérance μ =14 et
d’écart-type s
=
1,5.
1. Quelle est la
probabilité que Sofia mette moins de 14 minutes pour se rendre au
cinéma ?
P(14 < Tv) = 0,5.
2. Quelle est la
probabilité que Sofia mette entre 12 et 14 minutes pour se rendre au
cinéma ? On
arrondira le
résultat à 10−3.
P(12 < Tv < 14) =P(14 < Tv)- P(12 < Tv)=0,5 -0,0912
=0,4088 ~0,409.
Partie
C :
En jouant aux dés
Sofia hésite entre le bus et le
vélo. Elle décide de lancer un dé
équilibré à 6 faces.
Si elle obtient 1 ou 2, elle
prend le bus, sinon elle prend son vélo.
On note :
— B l’évènement « Sofia prend
le bus »;
— V l’évènement « Sofia prend
son vélo »;
— C l’évènement « Sofia met
entre 12 et 14 minutes pour se rendre au
cinéma ».
1. Démontrer que la
probabilité, arrondie à 10−2, que Sofia mette entre 12 et 14
minutes est de 0,49.
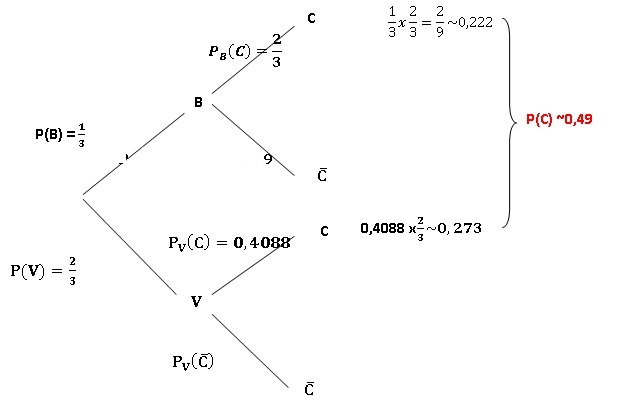
2. Sachant que
Sofia a mis entre 12 et 14 minutes pour se rendre au cinéma, quelle est
la probabilité, arrondie à 10−2, qu’elle ait emprunté le bus
?
PC(B) =P(C n B)
/ P(C) =0,222 / 0,49 ~0,45.
Amérique du Sud
Partie A :
Un organisme de contrôle sanitaire s’intéresse au nombre de bactéries
d’un certain type contenues dans la crème fraîche. Pour cela, il
effectue des analyses portant sur 10 000 prélèvements de 1 mL de crème
fraîche dans l’ensemble de la production française.
Les résultats sont donnés dans le tableau et représentés dans
l’histogramme ci-dessous :
Nombre
de bactéries ( milliers)
|
[100
; 120 [
|
[120
; 130[
|
[130
; 140 [
|
[140
; 150 [
|
[150
; 160 [
|
[160
; 180[
|
Nombre
de prélèvements
|
1597
|
1284
|
2255
|
1808
|
1345
|
1711
|
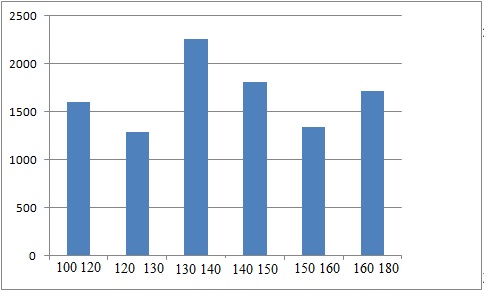
À l’aide de la calculatrice, donner une estimation de la moyenne et de
l’écart-type du nombre de bactéries par prélèvement.
Moyenne : (110 x1597 +125 x1284 +135 x2255 +145 x1808 +155 x1345 +170
x1711) / 10000 =140 milliers / mL.
Variance : 0,1597(140-110)2 +0,1284 (140-125)2
+0,2255(140-135)2+0,1808(145-140)2
+0,1345(155-140)2+0,1711(170-140)2 ~376.
Ecart type : 376½ ~19,15.
Partie B :
L’organisme décide alors de modéliser le nombre de bactéries étudiées
(en milliers par mL) présentes dans la crème fraîche par une variable
aléatoire X suivant la loinormale de paramètres μ = 140 et σ = 19.
1. a. Ce choix de
modélisation est-il pertinent ? Argumenter.
Ce choix est pertinent, on retrouve la moyenne et l'écart type des
résultats précédents.
b. On note p = P(X >160). Déterminer la
valeur arrondie de p à 10−3.
p(X > 160) = 1
-p(X <160) =
1-0,85374 ~0,146.
2. Lors de
l’inspection d’une laiterie, l’organisme de contrôle sanitaire analyse
un échantillon de 50 prélèvements de 1 mL de crème fraîche dans la
production de cette laiterie; 13 prélèvements contiennent plus de 160
milliers de bactéries.
a. L’organisme
déclare qu’il y a une anomalie dans la production et qu’il peut
l’affirmer en ayant une probabilité de 0,05 de se tromper. Justifier
sa déclaration.
n > 30 ; np = 50 x0,146 = 7,3 > 5 ; n(1-p) = 50 x0,854 = 42,7
> 5.
Les conditions sont requises pour établir un intervalle defluctuation
au seuil de 95 %.
1,96 (p(1-p) / n)½ = 1,96 (0,146 x0,854/ 50)½
=0,098
Intervalle de fluctuation au seuil de 95 % : [0,146 - 0,098
; 0,146 +0,098] soit :[0,00486 ;0,244 ]
13 / 50 =0,26. Cette valeur n'appartient pas à l'intervalle de
fluctuation. La déclaration est justifiée.
b. Aurait-il pu
l’affirmer avec une probabilité de 0,01 de se tromper ?
1,96 (p(1-p) / n)½ = 2,58 (0,146 x0,854/ 50)½
=0,129.
Intervalle de fluctuation au seuil de 99 % : [0,146 - 0,129 ;
0,146 +0,129] soit :[0,017 ;0,275 ] .
13 / 50 =0,26. Cette valeur appartient à l'intervalle de fluctuation.
La déclaration n'est pas justifiée.
|
|