Mathématiques,
probabilités, suite, fonction, géométrie, bac
S centres étrangers 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice
1. QCM.
On étudie la production d'une usine qui produit des
bonbons, conditionnés en sachets.
On choisit un sachet au hasard dans la production journalière. La masse
de ce sachet ( en g ), est modélisée par une variable aléatoire X qui
suit une loi normale d'espérance µ = 175. Une observation statistique a
montré que 2 % des sachets ont une masse inférieure ou égale à
170 g, ce qui se traduit par : P(X <170) = 0,02.
1. Quelle est la probabilité,
arrondie au centième, de l'événement " la masse d'un sachet est
comprise entre 170 et 180 g" ? 0,04 , 0,96 ; 0,98 ; on ne peut pas
répondre car il manque des données.
On pose Y = (X-175) / s
= -5 / s avec s l'écart type.
Y suit la loi normale centrée réduite ; P( Y < -5 / s)=0,02.
On utilise la touche " inverse loi normale" de la calculatrice pour
trouver : -5 / s =
-2,054.
Par suite s = 5 /
2,054 ~2,434.
P(170 < X < 180 ) =P(-2,054 < Y < 2,054) =1-0,02-0,02 = 0,96. Réponse b.
Les différents bonbons sont enrobés d'une cire commestible. Ce procédé,
qui déforme certains bonbons, est effectué par deux machines A et B.
Lorsqu'il est produit par A, la probabilité qu'un bonbon prélevé
aléatoirement soit déformé est égale à 0,05.
2. Sur un
échantillon aléatoire de 50 bonbons issus de A, quelle est la
probabilité, arrondie au centième, qu'au moins 2 bonbons soit déformés
? 0,72 ; 0,28 ; 0,54 ; on ne peut pas répondre car il manque des
données.
Soit Z la variable aléatoire comptant le nombre de bonbons déformés.
n = 50 tirages aléatoires, indépendantset identiques. deux issus
sont possibles :le bonbon est déformé p = 0,05 ; le bonbon n'est pas
déformé q = 1-p = 0,95.
La variable aléatoire Z suit une loi binomiale de paramètre n = 50 et p
= 0,05.
Au moins deux signifie : 2 et plus de deux.
P( Z >2) = 1-P(Z < 1) = 1-0,28 = 0,72 ; réponse a.
A produit un tiers des bonbons, B produit le reste.
Lorsqu'il est produit par B, la probabilité qu'un bonbon soit déformé
est égale à 0,02. On prélève au hasard dans la production un bonbon ;
celui-ci est déformé.
Quelle est la probabilité qu'il soit produit par B ? 0,02 ; 0,67 ; 0,44
;0,01.
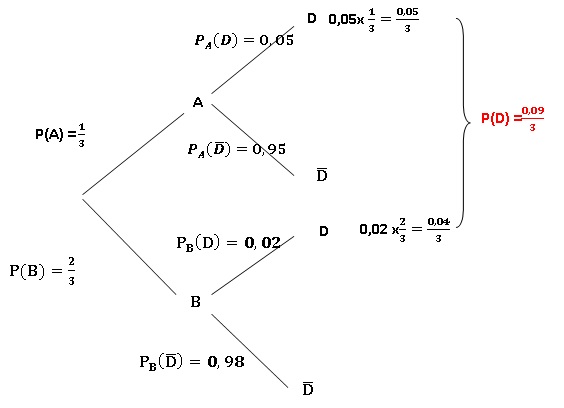
Probabilité que le bonbon
déformé soit produit par B : 0,04 / 0,09 ~0,44, réponse c.
La durée de vie de
fonctionnement ( en jours), d'une machine servant à l'emballage, est
modélisée par une variable aléatoire Y qui suit une loi exponentielle
dont l'espérance est égale à 500 jours.
4. Quelle est la
probabilité, arrondie au centième, que la durée de fonctionnement de la
machine soit inférieure ou égale à 300 jours ? 0,45 ; 1 ; 0,55 ; on ne
peut pas répondre car il manque des données.
l
= 1/500 = 0,002.
P( X < 300) =
1-exp(-0,002 x300) = 0,45, réponse a.
L'entreprise souhaite estimer la proportion de personnes de plus de 20
ans parmi ces clients, au niveau de confiance de 95 %, avec un
intervalle d'amplitude inférieure à 0,05. Elle interroge un échantillon
aléatoire de ces clients.
5. Quel est le
nombre minimal de clients à interroger ? 40 ; 400 ; 1600 ; 20.
Au seuil de 95%, intervalle de confiance (f-1/n½ ; f +1/n½].
Amplitude : 2 / n½ = 0,05 ; n½ = 2 / 0,05= 40 ; n
= 1600, réponse c.
|
| .
. |
....
.....
|
Exercice 2 .
L'espace est muni d'un repère
orthonormé. On considère deux droites d1 et d2
définies par leurs représentations paramétriques :
d1 : x=2+t ; y = 3-t ; z =t, avec t réel.
d2 : x = -5+2t' ; y = -1+t' ; z=5, avec t' réel.
On admet que ces droites
sont non coplanaires.
But de l'exercice
: existe-t-il une droite D
qui soit à la fois sécante avec d1 et d2 et
orthogonale à ces deux droites.
1. Vérifier que le
point A(2 ; 3 ; 0) appartient à d1.
xA=2 = 2 +t soit t=0 ; par suite y = 3-0 = 3 = yA
; z = 0 = zA.
2. Donner un
vecteur directeur de chaque droite. Ces droites sont-elles parallèles ?
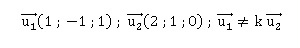
Ces vecteurs n'étant pas colinéaires, ces droites ne sont pas
parallèles.
3. Vérifier que le
vecteur de coordonnées (1 ; -2 ; -3) est orthogonal aux vecteurs
précédents.
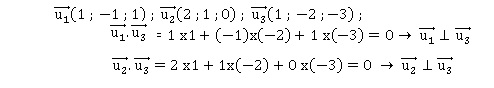
4. Soit P le plan
passant par le point A et dirigé par les vecteurs u1 et u3.
On étudie dans cette question l'intersection de la droite d2
avec ce plan P.
a. Montrer qu'une
équation cartésienne du plan P est 5x+4y-z-22 = 0.
Equation du plan P : ax +by +cz +d = 0.
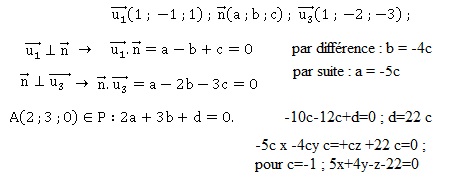
b. Montrer que la
droite d2 coupe le plan P en B(3 ; 3 ; 5).
5(-5+2t') +4(-1+t') -5-22=0 ; 14 t' = 56 ; t' = 4.
Par suite la droite d2 et le plan P se coupent au point de
coordonnées (3 ; 3 ; 5).
5. On consodère la
droite D de
vecteur directeur u3 (1 ; -2 ; -3) et passant par le point B.
a. Donner une représentation paramétrique de cette droite.
x = t" +xB = t"+3 ; y = -2t" +yB = -2t" +3 ; z =
-3t" +zB = -3t" +5 avec t" réel.
b. Les droites d1
et D sont-elles
sécantes ? Justifier.
Si ces droites sont sécantes :
x=2+t =t"+3 soit t = t"+1 ;
y = 3-t=-3-t"-1 = -2t"+3 soit t"=1 et t =2.
z =t =-3t"+5 ; 2 = -3+5 est bien vérifié.
Les droites d1 et
D sont
sécantes au point de coordonnées (4 ; 1 ; 2).
c. Expliquer
pourquoi la droite D
répond au problème.
D'après 3, la droite D
est orthogonales aux droites d1 et d2.
D'après 5b, les droites D et d1 sont
sécantes.
L'intersection de D et d2 est le
point B.
D est sécante avec les
droites d1 et d2 et orthogonale à ces droites.
|
|
|
Exercice
3.
La pharmacocinétique étudie l'évolution d'un médicament après son
administration dans l'organisme, en mesurant sa concentration
plasmatique.
A. Administration par voie
intraveineuse.
On note f(t) la concentration plasmatique ( en µg /L) du médicament ,
au bout de t heures après l'administration. le modèle mathématique est
f(t) = 20 e-0,1t avec t appartenant à [0 ; +oo[.
f(0) = 20 µg /L.
1. La demi-vie du
médicament est la durée en heure après laquelle la concentration
plasmatique du médicament est égale à la moitié de la concentration
initiale. Déterminer cette demi-vie t½.
10 = 20 e-0,1t½ ; ln(0,5) = -0,1 t½ ; t½
=10 ln 2 heures.
2. On estime que le
médicament est éliminé dès que sa concentration est inférieure à
0,2 µg / L.
Déterminer le temps à partir duquel le médicament est éliminé.
0,2 = 20 exp(-0,1t) ; ln 0,01 = -0,1 t ; t = -10 ln(0,01)~46,1 heures.
3. On appelle ASC (
ou aire sous la courbe ) le nombre suivant. Vérifier que l'ASC est égal
à 200 µg /L.h
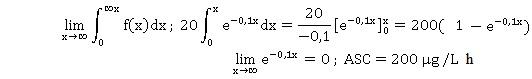
B. Administration par voie
orale.
On note g(t) la concentration plasmatique du médicament ( µg / L) au
bout de t heures après ingestion par voie orale. Le modèle mathématique
est g(t) = 20 (e-0,1t -e-t) avec t appartenant à
[0 ; +oo[. Dans ce cas g(0) = 0.
1. Démontrer que
pour tout t de cet intervalle, g'(t) = 20 e-t(1-0,1e0,9t).
g'(t) = 20 (-0,1 e-0,1t +e-t) =20
(-0,1 e(0,9-1)t +e-t) =20
(-0,1 e0,9t
e-t +e-t) =20
e-t(1-0,1e0,9t).
2. Etudier les
variations de la fonction g(t) sur cet intervalle. En déduire la durée
après laquelle la concentration est maximale ( à la minute près ).
20 e-t est toujours positif.
g'(x) <0 si 0,1e0,9t
>1 soit t > ln(10) / 0,9 = 2,558 heures ou 2 h
34 min.
g(x) est strictement décroissante sur [ 2,558 ; +oo[
g'(x) >0 si 0,1e0,9t <1 soit t >
ln(10) / 0,9 = 2,558 heures.
g(x) est strictement croissante sur [0 ; 2,558[
g't) est nulle si t = ln(10) / 0,9.
g(t) est maximale.
C. Administration répétée
par voie intraveineuse.
On décide d'injecter à intervalles de temps réguliers la même dose de
médicament par voie intraveineuse. l'intervalle de temps entre deux
injections est égal à la demi-vie du médicament.
Chaque nouvelle injection entraîne une hausse de concentration
plasmatique de 20 µg /L.
On note unn. la concentration plasmatique du médicament
immédiatement après la n-ième injection.
Ainsi u1 = 20 et un+1 = 0,5 un +20.
1. Démontrer par
récurrence que, pour tout entier n >1 :
un = 40 -40x0,5n.
Initialisation
: u1 = 20 ; la propriété est vraie au rang 1.
Hérédité :
la propriété est supposée vraie au rang p : up
= 40 -40x0,5p.
up+1 =
0,5 up +20 = 20-40x0,5p x0,5+20
up+1 =40
-40 0,5p+1 . la propriété est vraie
au rang p+1.
Conclusion
: la propriété est vraie au rang 1 et héréditaire.
La propriété est vraie pour tout n >1.
2. Déterminer la
limite de la suite (un) quand n tend vers l'infini.
-1 < 0,5 <1 ; par suite 0,5n tend vers zéro
quand n tend vers l'infini.
La suite tend vers 40 quand n tend vers l'infini.
3. On considère que
l'équilibre est atteint dès que la concentration plasmatique dépasse 38
µg /L. Déterminer le nombre minimal d'injections nécessaire pour
atteindre cet équilibre.
un
= 40 -40x0,5n =38 ; 2 / 40 = 0,5n ; n = ln(0,05)
/ ln(0,5 )~ 4,3.
Après 5 injections, l'équilibre est atteint.
|
|
|
|
Exercice4.
Le
plan est muni d'un repère orthonormé.
Pour tour entier n >4,
on consodère Pn
un polygone régulier à n côtés, de centre O dont l'aire est égale à 1.
On admet qu'un tel polygone est constitué de n triangles superposables
à un triangle OAnBn donné, isocèle en O.
On note rn = OAn la distance entre O et le sommet
An d'un tel polygone.
A. Etude du cas
particulier n = 6.
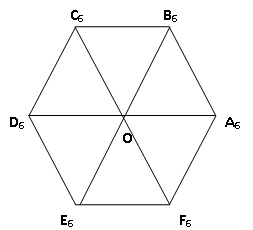
1. Justifier le
fait que le triangle OA6B6 est équilatéral et que
son aire soit égale à 1 /6.
Le triangle OA6B6 est isocèle en O et l'angle au
sommet mesure 60°. Ce triangle est donc équilatéral.
L'aire du polygone est égale à 1 ; ce polygone est constitué de six
triangles identiques. L'aire d'un triangle est égale à 1 / 6.
2. Exprimer en
fonction de r6 la hauteur du triangme OA6B6
issue du sommet B6.
Le triangle étant équilatéral, les hauteurs on même mesure ; les
hauteus sont également médiatrices des côtés.
Soit H le pied de la hauteur : OH2 +HB62
=OA62 ;
OH2 =r62- (0,5 r6)2=3
/ 4 r62 ; OH = 3½ /2
r6.
3. En déduire que r6
= [2 / (3 x3½)]½.
Aire du triangle OA6B6 = 1 / 6 = OH xA6B6
/2 = 3½ /4 r26.
r26 =2 /(3 x3½) ; r6 = [2 /
(3 x3½)]½.
B. Cas général avec n >4.
Le point An est situé sur l'axe réel et a pour affixe rn.
On note rn exp(iqn)
l'affixe de Bn.
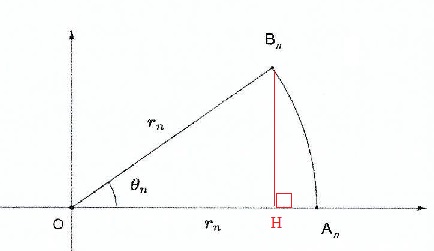
1. Exprimer en
fonction de rn et qn
la hauteur issue de Bn dans le triangle OAnBn,
puis établir que l'aire de ce triangle est égale à r2n
/ 2 sin (qn).
BnH = rn sin (qn) ; A = ½BnH
xOAn=r2n / 2 sin (qn).
2. Donner en
fonction de n, une mesure de l'angle qn, puis
démontrer que : rn = [2 / (n sin(2p /n))]½.
qn=
2p /n ; aire du
triangle OAnBn = 1 / n =r2n
/ 2 sin (qn).
1 / n =r2n / 2 sin (2p /n).
r2n =2 / (n sin(2p /n)) ; rn = [2
/ (n sin(2p /n))]½.
|
Partie C. Etude
de la suite (rn).
On considère la fonction f définie pour tout réel x de l'intervalle ]0
; p[ par f(x) = x / sin(x).
Ainsi rn = [1 /p
f(2p/n)]½.
On admet que f est strictement croissante sur ]0 ; p[.
Montrer que la suite (rn) est décroissante. On pourra
commencer par démontrer que pour n >4, 0 < 2p/(n+1) <p.
pour n >4, 0 < 2 < n < n+1 équivalent à : 0 <1
/ (n+1) < 1 / n < 0,5.
0 <2p
/ (n+1) < 2p / n < p.
f étant strictement croissante et strictement positive sur cet
intervalle : 0 <f(2p /
(n+1)) < f((2p / n).
0 < 1 / p
f(2p /
(n+1)) < 1 / p f((2p / n).
La fonction racine carrée est croissante sur [0 ; +oo[.
Par suite : 0 < [1 / p
f(2p /
(n+1))]½ < [1 / p f((2p / n)]½.
Soit 0 < rn+1 < rn. La suite (rn)
est donc décroissante.
2. En déduire que
cette suite converge. On ne demande pas de déterminer sa limite L et on
admet que L = p-½.
Cette suite est décroissante et de plus elle est
minorée par zéro. Cette suite converge donc.
3. On considère
l'algorithme suivant :
Variable : n est un nombre entier.
Traitement : n prend la valeur 4.
Tant que [2 / (n sin(2p
/n))]½ <0,58 faire
n prend la
valeur n+1
Fin Tant que
Sortie : Afficher n.
Quelle valeur numérique de n affiche cet algorithme ?

|
|