Mathématiques,
bac S métropole 09 /2017
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice 1. 6 points
Partie A.
On considère la suite (u n) définie pour
tout entier naturel n par : 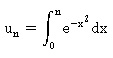
On ne cherchera pas à calculer u n en fonction de n.
1. a. Montrer que
la suite (u n) est croissante.
La fonction exp(-x 2) est continue et positive sur
l'intervalle [n ; n+1]. En conséquence u n >0.
u n+1-u n >0.
La suite est donc croissante.
b. Démontrer que
pour tout réel x >
0, on a : -x 2 <
-2x+1, puis : exp(-x 2) < exp(-2x+1). En déduire que pour tout entier
naturel n, on a : u n < ½e.
(x-1) 2 >
0 ; x 2-2x+1 >
0 ; x 2 >
2x-1 ; -x2 < -2x+1.
La fonction exponentielle étant strictement croissante sur R : exp(-x2) < exp(-2x+1).
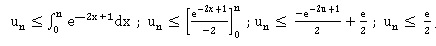
2 . c.
Démontrer que la suite (u n) est convergente. On ne cherchera
pas à calculer sa limite.
La suite (u n) étant croissante et majorée, elle converge.
2. Dans cette
question, on se propose d’obtenir une valeur approchée de u 2.
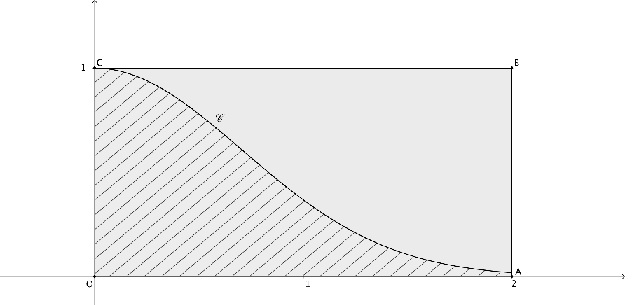
Dans le repère orthonormé , on a tracé la courbe
représentative de la fonction f
définie sur l’intervalle [0; 2] par f(x) = exp(-x 2), et le
rectangle OABC où A(2;0), B(2;1) et C(0;1).
On a hachuré le domaine D compris entre la courbe ,
l’axe des abscisses, l’axe des ordonnées et la droite d’équation x = 2.
On considère l’expérience aléatoire consistant à choisir un point M au
hasard à l’intérieur du rectangle OABC.On admet que la probabilité p
que ce point appartienne au domaine D est :
p = aire de D / aire OABC
a. Justifier que u 2
= 2p.
p = u 2 / (2x1) = u 2 / 2 ; u 2 =
2p.
b. On considère
l’algorithme suivant :
Variables : N, C nombres entiers ; X, Y, F nombres réels
Entrée : Saisir N
Initialisation : C prend la valeur 0
Traitement :
Pour k variant de 1 à N
X prend la valeur d’un nombre aléatoire entre 0 et 2
Y prend la valeur d’un nombre aléatoire entre 0 et 1
Si Y <
exp(-x 2) alors C prend la valeur C+1
Fin si
Fin pour
Afficher C
F prend la valeur C/N
Afficher F
i. Que permet de
tester la condition Si Y < exp(-x2) alors C prend la valeur C+1
concernant la position du point M(X;Y) ?
Le point M appartient-il au domaine D ?
ii. Interpréter la
valeur F affichée par cet algorithme.
F = fréquence des points situés dans le domaine D parmi N tirages au
sort.
iii. Que peut-on
conjecturer sur la valeur de F lorsque N devient très grand ?
F tend vers p si N devient très grand.
c. En faisant
fonctionner cet algorithme pour N = 10 6, on obtient C =
441138.
On admet dans ce cas que la valeur F affichée par l’algorithme est une
valeur approchée de la
probabilité p à 10 -3 près. En déduire une valeur approchée
de u 2 à 10 -2 près.
p ~441138 / 10 6 ; u 2=2x 441138 10 -6
~0,88.
|
| .
. |
....
...
|
Partie B.
Une entreprise spécialisée est chargée par l’office de tourisme d’une
station de ski de la conception d’un panneau publicitaire ayant la
forme d’une piste de ski.
Afin de donner des informations sur la station, une zone rectangulaire
est insérée sur le panneau comme indiqué sur la figure ci-dessous.
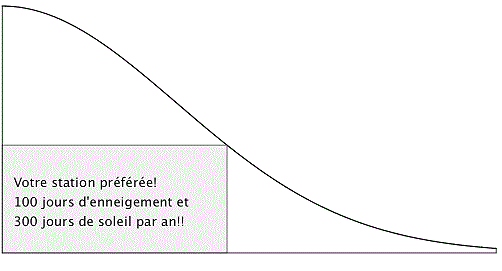
Le panneau, modélisé par le domaine D défini dans la Partie A, est
découpé dans une plaque rectangulaire de 2 mètres sur 1 mètre. Il est
représenté ci-dessous dans un repère orthonormé ; l’unité choisie est
le mètre.
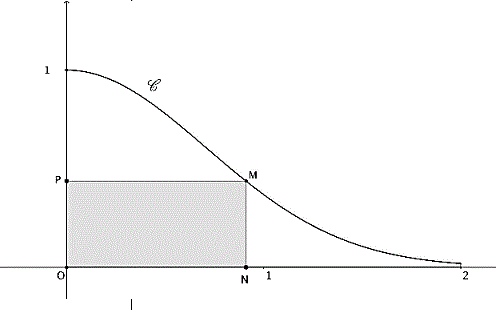
Pour x nombre réel appartenant à l’intervalle [0 ; 2], on note :
• M le point de la courbe de coordonnées
(x ; exp(-x2)),
• N le point de coordonnées (x; 0),
• P le point de coordonnées (0; exp(-x2)),
• A(x) l’aire du rectangle ONMP.
1. Justifier que
pour tout nombre réel x de l’intervalle 0; 2 , on a : A (x)=x exp(-x2).
A(x) = ON * OP = x exp(-x2)
2. Déterminer la position du point M
sur la courbe pour laquelle l’aire du rectangle ONMP est
maximale.
Dériver A(x). On pose u = x et v = exp(-x2) ;
u' = 1 ; v' = -2x exp(-x2).
u'v+v'u = exp(-x2) -2x2
exp(-x2) = exp(-x2) (1-2x2).
La dérivée s'annule pour x = 1 / 2½.
La fonction exponentielle est toujours positive. La dérivée est
positive si x appartient à [0 ; 1 / 2½], A(x) est croissante sur [0 ; 1 / 2½].
A(x) présente
un maximum pour x = 1 / 2½.
3.
Le rectangle ONMP d’aire maximale obtenu à la question 2. doit être
peint en bleu, et le reste du
panneau en blanc. Déterminer, en m2 et à 10-2
près, la mesure de la surface à peindre en bleu et celle de la surface
à peindre en blanc.
Le rectangle est peint en bleu : A = 1 / 2½ exp(-0,5) ~0,43 m2.
Aire peinte en blanc : 0,88 -0,43 = 0,45 m2.
|
|
|
Exercice
2 .( 4 points).
Le plan complexe est rapporté à un repère
orthonormé. À tout point M d’affixe z, on associe le
point M′ d’affixe z'= −z2 + 2z. Le point M′ est appelé image
du point M.
1. Résoudre dans
l’ensemble C des nombres complexes l’équation : −z2 + 2z − 2
= 0..
En déduire les affixes des points dont l’image est le point d’affixe 2.
Discriminant D =22-4(-2)(-1)
=-4 = 4 i2.
z1 = (-2 +2i)/(-2) = 1-i ; z2 = 1+i.Les points
dont l'image est le point d'affixe 2 vérifient :
z'=2 = -z2+2z soit -z2+2z-2=0.
Ce sont les points d'affixe 1+i et 1-i.
2. Soit M un point
d’affixe z et M′ son image d’affixe z′.
On note N le point d’affixe zN = z2.
Montrer que M est le milieu du segment [NM′].
Soit P le milieu du segment [NM'] ; l'affixe de P est :
zP = (zN +zM') / 2 = (z2−z2 + 2z) /2 = z.
Donc M est
le milieu du segment [NM′].
3.
Dans cette question, on suppose que le point M ayant pour affixe z,
appartient au cercle C de centre O et de rayon 1. On note q un argument de z.
a. Déterminer le
module de chacun des nombres complexes z et zN, ainsi qu’un
argument de zN en
fonction de q.
Module de z : |z| = 1. Argument de z : q ; z = 1 exp(iq).
zN = z2 = 1 exp(2iq).
Le module de zN vaut 1 et son argument 2q.
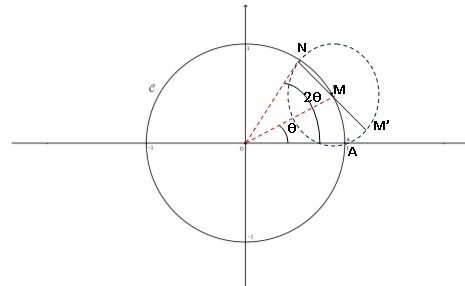
b. Sur la figure
donnée ci-dessous, on a représenté un point M sur le cercle C.
Construire
sur cette figure les points N et M′ en utilisant une règle et un compas
(on laissera les traits de construction apparents).
c. Soit A le point
d’affixe 1. Quelle est la nature du triangle AMM′ ?
M est le milieu du segment [NM'] ; MN=MM'.
N appartient au cercle de centre M et de rayon MA. ; MA = MN.
Par suite, MA = MM'; le triangle AMM' est isocèle en M.
|
|
|
|
Exercice 3. 5 points..
Tous les résultats
demandés seront arrondis au millième.
1. Une étude
effectuée sur une population d’hommes âgés de 35 à 40 ans a montré que
le taux de cholestérol total dans le sang, exprimé en grammes par
litre, peut être modélisé par une variable aléatoire T qui suit une loi
normale d’espérance µ = 1,84 et d’écart type s = 0,4.
a. Déterminer selon
cette modélisation la probabilité qu’un sujet tiré au hasard dans cette
population ait un taux de cholestérol compris entre 1,04 g/L et 2,64
g/L.
p(T <1,04) =
0,02275 ; p(T <2,64)
= 0,9772 ; p(1,04 <
T < 2,64) =
0,9772-0.02275 ~0,954.
b. Déterminer selon
cette modélisation la probabilité qu’un sujet tiré au hasard dans cette
population ait un taux de cholestérol supérieur à 1,2 g/L
p(T > 1,2) = 1 -p(T <
1,2) = 1-0,0668 ~0,945.
2. Afin de tester
l'efficacité d’un médicament contre le cholestérol, des patients
nécessitant d’être traités ont accepté de participer à un essai
clinique organisé par un laboratoire. Dans cet essai, 60 % des patients
ont pris le médicament pendant un mois, les autres ayant pris un
placebo (comprimé neutre). On étudie la baisse du taux de cholestérol
après l’expérimentation.
On constate une baisse de ce taux chez 80 % des patients ayant pris le
médicament.
On ne constate aucune baisse pour 90 % des personnes ayant pris le
placebo.
On choisit au hasard un patient ayant participé à l’expérimentation et
on note :
• M l’événement « le patient a pris le médicament » ;
• B l’événement « le taux de cholestérol a baissé chez le patient ».
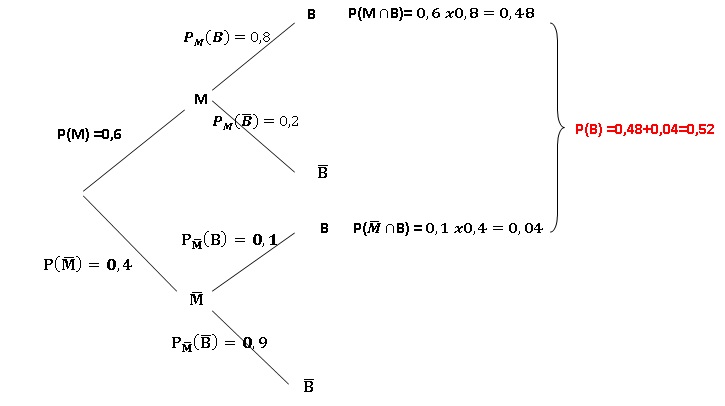
a. Traduire les
données de l’énoncé à l’aide d’un arbre pondéré.
b. Calculer la
probabilité de l’événement B.
c. Calculer la
probabilité qu’un patient ait pris le médicament sachant que son taux
de cholestérol a baissé.
pB(M)=p(M n B) / p(B) = 0,48 /0,52 = 12 / 13 ~0,923.
3. Le laboratoire
qui produit ce médicament annonce que 30 % des patients qui l’utilisent
présentent des effets secondaires.
Afin de tester cette hypothèse, un cardiologue sélectionne de manière
aléatoire 100 patients traités avec ce médicament.
a.
Déterminer l’intervalle de fluctuation asymptotique au seuil de 95 % de
la proportion de patients suivant ce traitement et présentant des
effets secondaires.
p =0,30 ; n =100 >
30 ; np = 30 > 5 ;
n(1-p) = 70 > 5.
1,96 (p(1-p) / n)½ = 1,96(0,3 x0,7 /100)½ =
0,0898.
Intervalle de fluctuation : [0,3 -0,0898 ; 0,30 +0,0898] soit [0,210 ;
0,390]
b. L’étude réalisée
auprès des 100 patients a dénombré 37 personnes présentant des effets
secondaires. Que peut-on en conclure ?
37/100 = 0,37. Ce nombre appatrient à l'intervalle de fluctuation. Au
risque de 5 %, on ne peut pas rejeter cette hypothèse.
c. Pour estimer la
proportion d’utilisateurs de ce médicament présentant des effets
secondaires, un organisme indépendant réalise une étude basée sur un
intervalle de confiance au niveau de confiance 95 %.
Cette étude aboutit à une fréquence observée de 37 % de patients
présentant des effets secondaires, et à un intervalle de confiance qui
ne contient pas la fréquence 30 %. Quel est l’effectif minimal de
l’échantillon de cette étude ?
Intervalle de confiance : [ f -1/n½ ; f +1/n½].
0,30 n'appartient pas à cet intervalle : 0,30 < 0,37 -n-½
; n-½ < 0,07 ; n½ >1/0,07 ; n > 205.
|
Exercice 5.
5 points
Dans l’espace, on
considère le cube ABCDEFGH représenté ci-dessous.
On note I et J les milieux respectifs des segments [EH] et [FB].
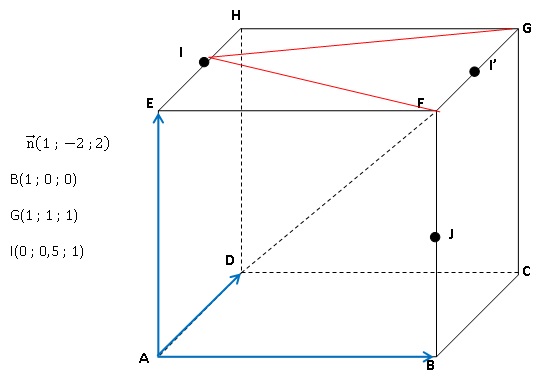
1. Donner les
coordonnées des points I et J.
E(0 ; 0 ; 1) ; H(0;1 ; 1 ) ; I milieu de [EH] : I((0+0) / 2 ; (0+1) / 2
; (1+1) / 2 ) ; I( 0 ; 0,5 ; 1).
B(1 ; 0 ; 0) ; F( 1 ; 0 ; 1) ; J milieu de [FB] ; J((1+1)/2
; (0+0) / 2 ; (0+1) /2) ; J (1 ;
0 ; 0,5) ;
2. a. Montrer que le vecteur nest un
vecteur normal au plan (BGI).
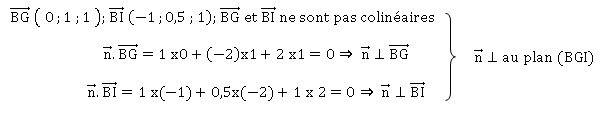
b. En déduire une
équation cartésienne du plan (BGI).
x-2y+2z+d=0.
B(1 ; 0 ; 0) appartient à ce plan : 1+0+0+d=0 d'où d = -1.
Equation du plan (BGI) : x-2y+2z-1=0.
c. On note K le
milieu du segment [HJ]. Le point K appartient-il au plan (BGI) ?
H(0 ; 1 ; 1) ; J(1 ; 0 ; 0,5) ; K milieu de [HJ] ; K((0+1) / 2 ; (1+0)
/ 2) ; (1+0,5) / 2) ; K( 0,5 ; 0,5 ; 0,75).
xK-2yK+2zK -1=0,5-1+1,5 -1=0.
Les coordonnées de K vérifient l'équation du plan ( BGI) : K appartient
donc à ce plan.
3. Le but de cette
question est de calculer l’aire du triangle BGI.
a. En utilisant par
exemple le triangle FIG pour base, démontrer que le volume du tétraèdre
FBIG est égal à 1 / 6.
IG=IF ; le triangle FIG est isocèle en I. L'aire de ce triangle vaut :
½ II' xFG = 0,5 x1 x1 = 0,5.
Volume du tétraèdre FBIG = base x hauteur / 3 = aire du triangle FIG x
BF / 3 = 0,5 x1 / 3 = 1 / 6.
b. Déterminer une
représentation paramétrique de la droite D passant par F et
orthogonale au plan (BGI).
Le vecteur n est un vecteur directeur de cette droite et cette droite
passe par F (1 ; 0 ; 1).
Représentation paramétrique de cette droite :
x = t+1 ; y =-2t ; z =2t+1 avec t réel.
c. La droite D coupe le plan (BGI) en F′.
Montrer que le point F′ a pour coordonnées (7 /9 ; 4 / 9 ; 5 / 9).
F'
appartient au plan ( BGI) et à la droite D : xF'-2yF'+2zF'
-1=0.
1+t -2(-2t)+2(2t+1)-1 = 0 ; 1+t+4t+4t+2-1=0 ; 9t +2=0 ; t = -2 /9.
Par suite xF'=-2/9+1=7/9 ; yF' =-2(-2/9) = 4 / 9
; zF' = 2(-2/9)+1=5/9.
d. Calculer la longueur FF′. En
déduire l’aire du triangle BGI.
F( 1 ; 0 ; 1) ; F'(7 /9 ; 4 /9 ; 5 /9) ; F'F =[(7/9-1)2+(4/9-0)2+(5/9-1)2]½=[(-2/9)2+(4/9)2+(4/9)2]½=(4+16+16)½
/ 9 =6 / 9 = 2 /3.
Volume du tétraèdre FBIG = aire du triangle BGI x FF' / 3 = 1 / 6 ;
aire du triangle BGI =( 3 /6 ) / (2 /3) = 3/4.
|
|