Mathématiques,
bac S Polynésie 09 /2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice
1. 6 points.
Un
parc d’attraction propose à son public un tout nouveau grand huit. Pour
des raisons de sécurité, son accès n’est autorisé qu’aux personnes dont
la taille est supérieure ou égale à 1,40 m et dont l’âge est compris
entre 10 et 70 ans. Des études statistiques sont menées pour évaluer
l’affluence et la satisfaction des visiteurs pour
ce manège. On arrondira, si nécessaire, les probabilités à 10-4.
1.a) La taille en
centimètres d’un visiteur du parc, choisi au hasard, est modélisée par
la variable aléatoire T qui suit la loi normale d’espérance 165 et
d’écart-type 20.
Quelle est la probabilité qu’un visiteur ait la taille requise pour
accéder à ce grand huit ?
P(T > 140) = 1
-P(T < 140)
=1-0,10565 =0,8944.
b) L’âge d’un
visiteur du parc, choisi au hasard, est modélisé par la variable
aléatoire X qui suit la loi normale d’espérance 30 et d’écart-type 17.
Quelle est la probabilité qu’un visiteur ait l’âge requis pour accéder
à ce grand huit ?
P(10 <
X < 70) = P(X < 70) -P(X <10)=0,99069-0,1197 =0,8710.
c)
Les études menées permettent d’établir que 89% des visiteurs ont la
taille exigée, 87% ont l’âge requis mais 8 % n’ont ni la taille, ni
l’âge obligatoires. Quelle est alors la proportion des visiteurs
vérifiant les conditions requises pour essayer la nouvelle attraction ?
|
T
>
140
|
T
< 140
|
Total
|
10
<X
<70
|
84
|
3
|
87
|
X
<10 et X >70
|
5
|
8
|
13
|
Total
|
89
|
11
|
100
|
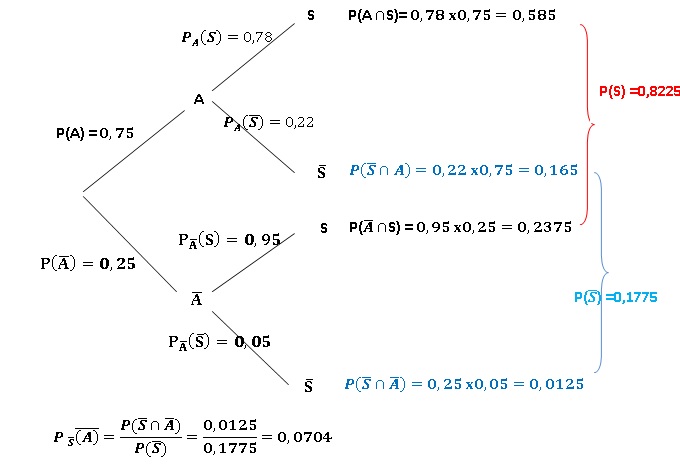
2. Un sondage est
réalisé à la sortie du grand huit et révèle que 25% des personnes ont
attendu moins de 30 min avant de pouvoir essayer le manège. Parmi
elles, 95 % sont satisfaites de l’attraction.
En revanche, 22 % des personnes ayant attendu plus de 30 min ne sont
pas satisfaites de l’attraction.
On choisit au hasard un visiteur à sa sortie du grand huit.
On note A l’événement « le visiteur a attendu plus de 30 min » et S
l’événement « le visiteur est satisfait de l’attraction ».
a) Montrer que la
probabilité qu’un visiteur soit satisfait de l’attraction vaut 0,8225.
b) Le directeur
rencontre un visiteur insatisfait. Quelle est la probabilité que ce
visiteur ait attendu moins de 30 min ?
3. Le directeur est
soucieux de savoir si le temps d’attente, plus important les jours de
grande affluence, remet en cause le taux de satisfaction des visiteurs.
Pour cela, on interroge 200 personnes au hasard à la sortie du grand
huit. Parmi elles, 46 se disent insatisfaites. Le directeur peut-il
être rassuré ?
n=200 > 30 ; p = 0,1775 (
proportion d'insatisfaits) ; np = 35,5 > 5 ; n(1-p)=164,5 > 30.
Les conditions sont vérifiées pour établir un intervalle de fluctuation
asymptotique au seuil de 95 % de la proportion de visiteurs
insatisfaits.
1,96 (p(1-p) / n)½ = 1,96 x(0,1775x0,8225/200) ½=0,053.
Intervalle de fluctuation [0,1775-0,053 ; 0,1775+0.053] soit [0,1245 ;
0,2305].
46 / 200 = 0,23, cette valeur appartient à l'intervalle précédent : au
risque de 5 %, le directeur est rassuré.
|
| .
. |
....
.....
|
Exercice 2. 6 points.
Partie A.
On s’intéresse à l’évolution au cours du temps d’une tumeur composée de
cellules cancéreuses.On
note N(t ) le nombre de cellules cancéreuses après un temps t exprimé
en semaines et N(0) = N0
le nombre de cellules cancéreuses au premier examen. Pour tout réel t
positif ou nul, on admet
qu’il existe un nombre a tel que N(t ) = N0 eat .
1. Des cultures en
laboratoire ont montré que le nombre de cellules de la tumeur double en
14 semaines. En déduire la valeur du paramètre a.
2N0 = N0 e14a ; 2= e14a ; ln2 = 14 a
; a = ln2 / 14 ~0,0495.
2. En arrondissant la valeur de a
obtenue, on peut écrire pour tout réel t > 0, N(t ) = N0 e0,05t
.
La plus petite tumeur détectable au toucher contient environ 109
cellules. Lorsqu’une tumeur est détectable, on décide d’opérer le
patient afin de la retirer. Or, après intervention, il est possible
qu’il reste jusqu’à 104 cellules indétectables. En l’absence
de suivi médical, au bout de combien de temps la tumeur pourrait-elle
redevenir détectable au toucher ?
109=104 e0,05 t ; ln109-ln104 =0,05 t
; t = ln(105)
/0,05 ~230 semaines.
Partie B.
Pour atténuer le risque de récidive, le médecin peut proposer de
compléter l’opération par une
chimiothérapie. Lors d’un traitement par chimiothérapie en
intraveineuse, la concentration du
médicament dans l’organisme, exprimée en µmol L-1, peut être
modélisée en fonction du temps t ,
exprimé en heure, par la fonction c définie sur l’intervalle [0 ;+oo[
par
c(t ) =D / k(1-exp(-kt/80)) où
• D est un réel positif qui représente le débit d’écoulement du
médicament dans la perfusion,
exprimé en micromole par heure ;
• k est un réel positif qui représente la clairance du patient,
exprimée en litre par heure.
La clairance traduit la capacité interne du patient à éliminer plus ou
moins vite le médicament de son organisme. Elle est propre à chaque
individu et est inconnue au début du traitement. Il est
nécessaire de la déterminer afin que le médecin puisse adapter le
traitement en ajustant le débit D.
1. Détermination
de la clairance
Afin de déterminer la clairance, on effectue les mesures suivantes. On
règle le débit de la perfusion
sur 112 µmol h-1 ; au bout de 6 heures, on prélève un
échantillon de sang du patient et on mesure la concentration du
médicament : elle est égale à 6,8 µmol L-1.
a) Justifier que la
clairance k du patient est solution de l’équation 112(1-exp(-3k /
80))-6,8 k=0.
c(6)=D / k(1-exp(-6k / 80))
=6,8 ;
112 / k (1-exp(-3k / 40)) = 6,8 ;
112(1-exp(-3k / 40))-6,8 k=0.
b) Démontrer que cette équation
admet une unique solution sur l’intervalle ]0 ;+oo[.
On note f(x) = 112(1-exp(-3x / 40))-6,8 x.
f '(x) = 112 x3 / 40 exp(-3x / 40)-6,8 = 8,4exp(-3x / 40)-6,8.
f '(x) = 0 pour : exp(-3x
/ 40) = 6,8 / 8,4= 17 / 21
x = -40 / 3 x ln (17 / 21) ~2,82.
f '(x) >0 si x < 2,82 : f(x) strictement croisante sur [0 ; 2,82[.
f '(x) < 0 si x > 0,282 ; f(x) strictement décroissante sur ]2,82
; +oo [.
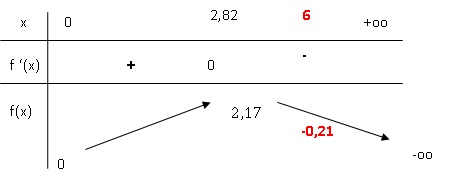
D'après ce tableau de variation, l'équation proposée admeet une seule
solution sur ]0 ; +oo[.
c) Donner une valeur approchée à 10-2
de cette solution. Interpréter ce résultat.
x
|
5
|
5,8
|
5,85
|
5,9
|
f(x)
|
1,02
|
0,07
|
0,00
|
-0,07
|
Pour une clairance de 5,85 L
h-1 et un débit de 112 µmol L-1, la concentration
du médicament est de 6,8 µmol L-1 au bout de 6 heures.
|
|
|
2. Réglage
du débit
a) Déterminer la
limite l de la
fonction c en +oo en fonction du débit D et de la clairance k.
c(t ) =D / k(1-exp(-kt/80))
k étant positif, quand t tend vers l'infini :
-kt / 80 tend vers moins l'infini et en conséquence exp(-kt/80)
tend vers zéro.
l = D / k.
b) La concentration du médicament
dans le sang se rapproche rapidement de sa limite l.
Pour que le traitement soit efficace sans devenir toxique, cette
concentration limite doit être de 16 µmol.L-1. En déduire le
débit D, à régler par le médecin, lorsque la clairance du patient est
de 5,85 L.h-1.
16 = D / 5,85 ; D = 16 x5,85 = 93,6
µmol h-1.
|
|
|
|
Exercice
3. 3 points.
On rappelle que pour tout réel a et tout réel b, cos(a -b) =
cos(a)cos(b)+sin(a)sin(b).
Le plan est rapporté à un repère orthonormé direct. On considère la
droite D d’équation y = -x+2.
1. Montrer que si
le réel µ appartient à l’intervalle ]-p/4 ; 3p/4 [ , alors cos(q-p/4)>0.
-p/4 < q < 3p/4 ; -p/4 -p/4 < q -p/4 < 3p/4 -p/4 ;
-p/2 < q -p/4 < p/2 ; donc cos(q-p/4)>0.
2. Soit M un point
du plan complexe d’affixe z non nulle. On note r =|z| le module de z et q= arg(z) un argument de z ;
les nombres r et q sont appelés coordonnées
polaires du point M.
Montrer que le point M appartient à la droite D si et seulement si ses
coordonnées polaires sont liées par la relation :
r = 2½
/ cos(q-p/4).
z = x + iy = r (cosq +i sin q) avec -p/4 < q < 3p/4.
cos(q-p/4) = cos(q)cos(p/4)+sin(q)sin(p/4)= 2½ / 2 (cosq + sin q).
M ( x ;y) appartient à la droite D : y = -x+2 soit x + y = 2.
x = r cos q ; y = r sin q ; 2 = r (sin q + cos q ) = 2r / 2½ cos(q-p/4).
r = 2½
/ cos(q-p/4).
Réciproquement on suppose que r
= 2½ / cos(q-p/4).
r
cos(q-p/4) =2½ ; r 2½ /
2(cosq + sin q)=2½ ;
r
(cosq + sin q) = 2 soit x +y = 2.
Donc M appartient à la droite D.
3. Déterminer les
coordonnées du point de la droite D le plus proche de l’origine O du
repère.
La distance OM est minimale si OM2 est minimum.
OM2 = x2 +y2 = x2 +(-x+2)2
= 2x2-4x+4= 2(x2-2x+2).
x2-2x+2, polynome du type ax2+bx+c, admet
un minimum pour x = -b / (2a) = 2 /2 =1. Par suite y = -x+2=1.
Le point M (1 ; 1) de la droite D est le plus proche de l'origine.
Exercice 4. 5
points.
On s’intéresse à une population de tortues vivant sur une île et dont
le nombre d’individus diminue de façon inquiétante.
Partie A.
Au début de l’an 2000, on comptait 300 tortues. Une étude a permis de
modéliser ce nombre de tortues par la suite (un) définie par
:
u0 = 0,3 et un+1 = 0,9un(1-un)
où pour tout entier naturel n, un modélise le nombre de
tortues, en milliers, au début de l’année 2000+n.
1. Calculer, dans ce modèle, le
nombre de tortues au début de l’année 2001 puis de l’année 2002.
u1=0,9 u0(1-u0)=0,9 x0,3(1-0,3)=0,189. ( 189 tortues )
u2=0,9 u1(1-u1)=0,9 x0,189(1-0,189)~0,138. ( 138 tortues ).
2. On admet que,
pour tout entier naturel n, un et 1-un
appartiennent à l’intervalle [0 ;1].
a) Montrer que,
pour tout entier naturel n, 0 <
un+1 <
0,9un.
0 < un < 1 ; 0 < 1-un < 1 ; on multiplie les
trois membres par un > 0.
0 < un(1-un)
< un
; 0 < 0,9 un(1-un)
< 0,9 un
; 0 < un+1
< 0,9un.
b) Montrer que,
pour tout entier naturel n, 0 <
un <
0,3 x0,9n.
Initialisation
: 0 < u0
< 0,3
x0,90. La propriété est vraie au rang zéro.
Hérédité.
La propriété est supposée vraie au rang p : 0 < up < 0,3 x0,9p.
0 < up+1
< 0,9up
; 0 < up+1
< 0,9
x0,3 x0,9p ; 0 < up+1 < 0,3 x0,9p+1
.
La propriété étant vraie au rang p+1, elle est héréditaire.
Conclusion
: la propriété est vraie au rang zéro et héréditaire, donc 0 < un < 0,3 x0,9n.
c) Déterminer la
limite de la suite (un). Que peut-on en conclure sur
l’avenir de cette population de tortues ?
-1 < 0,9 <1, donc 0,9n tend vers zéro quand n tend
vers l'infini.
0 < un < 0,3 x0,9n.
Donc, d'après le théorème des gendarmes, la suite (un) tend
vers zéro, quand n tend vers l'infini.
Les tortues vont toutes disparaître.
3. Des études
permettent d’affirmer que, si le nombre de tortues à une date donnée
est inférieur au seuil critique de 30 individus, alors l’espèce est
menacée d’extinction.On souhaite qu’à la fin de son exécution,
l’algorithme ci-dessous affiche la dernière année avant laquelle il
reste au moins 30 tortues. Recopier et compléter l’algorithme afin
qu’il satisfasse cette exigence.
Variables : u est un réel
n est un entier naturel
Traitement : u prend la valeur 0,3
n prend la valeur 0
Tant que u >0,03
faire :
n prend la
valeur n+1
u prend la
valeur 0,9u(1-u)
Fin Tant que
Sortie : Afficher n-1.
|
Partie B
Au début de l’année 2010, il ne reste que 32 tortues. Afin d’assurer la
pérennité de l’espèce, des actions sont menées pour améliorer la
fécondité des tortues. L’évolution de la population est alors modifiée
et le nombre de tortues peut être modélisé par la suite (vn)
définie par :
v10 =0,032 et vn+1 = 1,06 vn(1-vn)
où pour tout entier naturel n >
10, vn modélise le nombre de tortues, en milliers, au début
de l’année 2000+n.
1. Calculer le
nombre de tortues au début de l’année 2011 puis de l’année 2012.
v11 = 1,06 v10(1-v10)
=1,06 x0,032 (1-0,032) =0,03283456 ( environ 33 tortues).
v12 = 1,06 v11(1-v11)
=1,06 x0,03283 (1-0,03283) =0,03366 ( environ 34 tortues).
2. On
admet que, dans ce modèle, la suite (vn) est croissante et
convergente. On appelle l
sa limite. Montrer que l
vérifie :
l=1,06 l(1-l).
Quand n tend vers l'infini : vn tend vers l ; 1-vn tend
vers 1-l ; 1,06 vn(1-vn)
tend vers l=1,06 l(1-l).
vn+1 tend vers l
; la limite étant unique : l=1,06 l(1-l).
3. La
population de tortues est-elle encore en voie d’extinction ?
La suite est croissante et v10 = 0,032; vn >
0,032 pour tout n >
10.
Il y aura donc au moins 32 tortues au delà de l'année 2010. La
population n'est plus en voie d'extinction.
|
|