|
expérience
de Melde modifiée
:
Utiliser les
résultats précédents pour
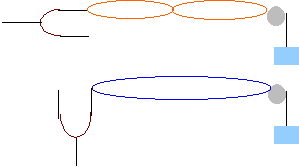
interpréter l'expérience
schématisée ci-dessous, c'est à dire
pour comparer le second montage à l'expérience
plus classique de Melde représenté
au-dessus.
Ordre de
grandeur: la corde a une masse linéïque de 0,8 g
/ m, une longueur utile de 0,5 m et est tendue par le poids
d'une masse de 50 g. Le diapason représente un
système qui vibre à la fréquence de 50
Hz.
corrigé
Pour le
premier cas, la corde oscille à la fréquence
du vibreur : il y a résonance lorsque le vibreur a
une fréquence égale à l'une des
fréquences propres de la corde. Les fréquences
propres sont données par :
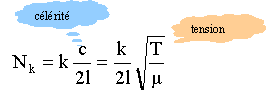
2l = 1
mètre; m=
8 10-4 kg/m
; T=
0,05*9,8 = 0,49 N
Nk
= 25 k Hz, k est un entier
pour k=2 (2
fuseaux) la relation est vérifiée pour une
fréquence de 50 Hz.
Dans le
second cas la tension varie de manière
sinusoïdale ; phénomène de
"résonance paramètrique ": la corde vibre une
fréquence égale à la moitié de
celle du vibreur, soit 25 Hz
retour
- menu
|