réactions d'addition sur les alcènes cinétique de substitution SN2 comparaison des pouvoirs nucléophiles de I- et Br- méthode potentiométrique : détermination de k1 polarimétrie : détermination de k2.d'après Mines En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .

réactions d'addition sur les alcènes Addition du dibrome sur un alcène : - Ecrire les formules topologiques des alcènes non cycliques de formule C4H8. Les nommer. - L'addition du Br2sur l'un de ces alcènes, noté C conduit à un seul dibromoalcane à chaîne carbonée linéaire. Identifier C en justifiant. Addition du bromure d'hydrogène sur l'alcène C dans un solvant polaire. - Ecrire le mécanisme de l'addition. - On obtient la molécule D : 2-bromobutane (S) : écrire la représentation spatiale de Cram. On obtient une autre molécule D' : identifier D'. 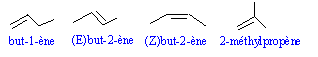corrigé Le 2-méthylpropène conduit à un dérivé dibromé à chaine ramifié ; le but-1-ène conduit au 1,2-dibromobutane racémique ; le (Z) but-2-ène conduit à deux énantiomères : (2R, 3R 2,3-dibromobutane et le (2S, 3S) 2,3-dibromobutane. C est le (E) but-2-éne : il conduit a un composé méso, achiral.   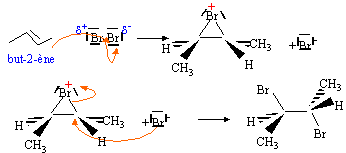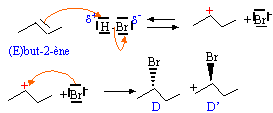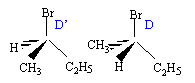addition de H-Br sur le (E) but-2-ène dans un solvant polaire ordre de priorité des groupements : -Br , -C2H5 , CH3 et H D est le (S) 2-bromobutane ; D' est le (R) 2-bromobutane; D et D' sont deux énantiomères.

cinétique de substitution SN2 Etude de l'action des ions iodures sur le (S) 2-bromobutane, noté D, dans un solvant peu polaire et aprotique. Le solvant : - Définir solvant polaire et protique ? Citer deux exemples. -Quel est l'intéret d'utiliser un solvant peu polaire et aprotique dans le cadre d'un mécanisme SN2 ? Schéma réactionnel : (1) D+I- --k1-->E + Br-. (2) E+I- --k2-->E' + I- ; (2') E'+I- --k'2-->E + I- . (3) E+Br- --k3-->D + I- ; (3') E'+Br- --k'3-->D' + I- ; (1') D'+I- --k'1-->E' + Br- ; (4) D+Br- --k4-->D' + Br- ; (4') D'+Br- --k'4-->D + Br- ; - Identifier E et E'. Comment appelle-t-on ces molécules ? - Justifier que k1 = k'1 ; k2 = k'2 , k3 = k'3 ; k4 = k'4. corrigé Un solvant polaire est un solvant dont le moment dipolaire n'et pas nul ( le barycentre des charges négatives ne coincide pas avec celui des charges positives). Un solvant protique est un solvant possédant des hydrogènes ayant un caractère acide ( H lié à un atome électronégatif comme l'oxygène ou l'azote) ; dans ce type de solvant les anions sont facilement solvatés. exemples de solvants protiques et polaires : acide éthanoïque et éthanol. Un solvant polaire, protique solvate d'autant plus les anions que leur charge est plus forte et plus localisée. Les réactifs étant fortement solvatés, le complexe activé est peu stabilisé ( énergie d'activation plus grande et réaction plus lente). 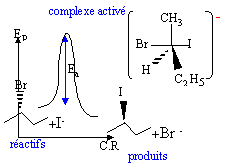E est le (R) 2-iodobutane obtenu à partir de D par un mécanisme SN2 ( inversion de configuration); E' est le (S) 2-iodobutane obtenu à partir de D' par un mécanisme SN2 ( inversion de configuration); E et E' sont deux énantiomères. Deux énantiomères ont les mêmes propriétés chimiques vis à vis de réactifs nucléophiles achiraux ( I- et Br- ) : donc les réactions (1) et (1') ont la même vitesse ; il en est de même pour (2) et (2') , (3) et (3') ainsi que (4) et (4').

comparaison des pouvoirs nucléophiles de I- et Br-   On donne les numéros atomiques Z(I)=53 et Z(Br)=35 Définir nucléophile. Quelle est la configuration électronique des ions I- et Br-.  - Calculer la charge effective Z* associée au dernier groupe de Slater occupé par les électrons. - La valeur du rayon d'un ion est : r = n*² / Z* a0 avec a0 = 53 ppm. Calculer r(I-) et r(Br-) - Comparer ces résultats aux valeurs espérimentales r(I-)= 216 ppm et r(Br-)= 195 ppm. Conclure quant à l'approximation de Slater ? - Justifier que les ions I- sont plus nucléophile que les ions Br-. Quelles réactions peut-on négliger dans le schéma réactionnel.   corrigé Un nucléophile est une espèce possédant des doublets non liants ; elle réagit avec des sites déficients en électrons ( site électrophile). Le pouvoir nucléophile est d'autant plus grand que la vitesse de l'attaque nucléophile est grande. configuration électronique : Br- : 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6. s4s,4p= 7*0,35 + 18*0,85 +8*1+2*1= 27,75 ; Z*4s,4p= 35-s4s,4p= 7,25. I- : 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2 5p6. s5s,5p= 7*0,35 + 18*0,85 +28*1= 45,75 ; Z*5s,5p= 53-s5s,5p= 7,25. r(Br-) = n*² / Z* a0 = 3,7² / 7,25*53 = 100 ppm écart avec la valeur expérimentale : 49% r(I-) = n*² / Z* a0 = 4² / 7,25*53 = 120 ppm écart avec la valeur expérimentale : 44% La différence entre les valeurs est dans le même sens (I- plus gros que Br-) : l'approximation de Slater est très approximative, mais permet de comparer les rayons des ions. Les électrons périphériques de I- sont plus éloignés du noyau et subissent la même charge effective que dans Br- : en conséquence, ils sont plus disponibles pour une attaque nucléophile ; I- est plus polarisable ( son nuage électronique se déforme sous l'influence d'un champ électrique extérieur); I- plus gros est moins solvaté et donc plus disponible pour une attaque nucléophile. il est raisonable de négliger les réactions (3), (3'), (4) et (4') du schéma réactionnel où intervient le nucléophile Br-.

méthode potentiométrique : détermination de k1. On étudie la cinétique précédente, seules les réactions (1), (2) et (2') interviennent. A t=0, on introduit dans V= 200 mL de solvant n1=0,05 mol de D et n2 = 0,1 mol d'iodure de sodium NaI . A de dates ti, on prélève du milieu réactionnel un échantillon de volume v0 = 10 mL. On le refroidit et on le dose par une solution aqueuse de nitrate d'argent AgNO3 de concentration cAg=0,2 mol/L. 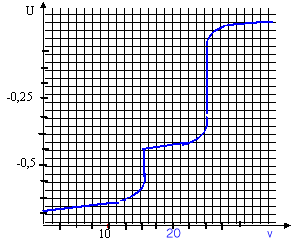Le suivi du dosage est suivi par une méthode potentiométrique où l'on observe la différence de potentiel U= EAg-Eréf entre une électrode d'argent et une électrode de référence en fonction du volume v de nitrate d'argent ajouté. On obtient pour l'instant t= 20 min la courbe ci-dessous :   Shématiser le dispositif du dosage. Exprimer U en fonction de [Ag+], Eréf et du potentiel standart E0 du couple Ag+/Ag. L'échantillon à doser contient les ions I- et Br- qui peuvent précipiter en présence des ions Ag+.: pKs1(AgI)= 16,1 ; pKs2(AgBr) = 12,3. Pour des concentrations en Br- et I- du même ordre de grandeur dans l'échantillon à doser, quel précipité apparaît en premier dans le dosage ? Selon quelle réaction R1 ? Justifier. - On note ve le volume où le deuxième précipité commence à se former. Quel est le point correspondant sur le graphe ? Relever ve. En déterminant le rapport [I-] / [Br-] montrer qu'en ce point R1 est presque terminée. - Donner la relation entre cAg, ve et nI- ( nI- : nombre de moles d'ion iodure dans l'échantillon). En déduire à l'instant t3, la relation donnant la concentration en iodure dans le milieu réactionnel [I-]M en fonction de cAg, ve et v0. Dans le milieu réactionnel on note les concentrations : a= [D]M à t==0 ; b = [I-]M à t =0 et x = [I-]M à t quelconque. On donne les concentrations des ions iodures, obtenues par la méthode précédente en fonction du temps : t(min) 0 5 10 20 40 80 infini x mol/L 0,422 0,375 0,277 0,255 - Exprimer et calculer numériquement a et b. Que peut-on dire de l'effet des réactions (2) et (2') sur les quantités d'ion iodure ? En déduire les concentrations [D] et [Br-] à l'instant t en fonction de a, b et x. - Compléter le tableau. - Déterminer l'équation différentielle vérifiée par x, l'intégrer et en déduire l'expression de t en fonction de x, a, b et k1. En déduire k1 ( en L mol-1 s-1) par une méthode non graphique. On présentera les valeurs utilisée sous forme de tableau. 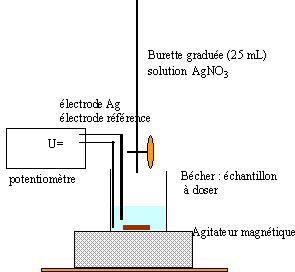corrigé potentiel relatif à l'électrode d'argent ( formule de Nernst) U =E0(Ag+/Ag) + 0,06 ln [Ag+]-Eréf. le précipité le moins soluble ( de pKs le plus grand) apparaît le premier : c'est à dire AgI selon la réaction R1 : Ag+ + I- = AgI (solide) K10 = 1/([I-][Ag+])= 1/ Ks1 = 1016,1. la seconde réaction de dosage est R2 : Ag+ + Br- = AgBr (solide) K20 = 1/([Br-][Ag+])= 1/ Ks2 = 1012,3. Le point anguleux du graphe (ve=16 mL) correspond à l'apparition du second précipité. En ce point les deux précipités sont présents donc : Ks1 =[I-][Ag+] et Ks2 = [Br-][Ag+] soit : [I-] / [Br-] = Ks1/Ks2 = 10-16,1 / 10-12,3=10-3,8. la concentration en I- est très inférieure à celle en Br- : R1 est pratiquement terminée. a = 0,05 / 0,2 = 0,25 mol/L ; b = 0,1 / 0,2 = 0,5 mol/L effet des réactions (2) et (2') : il se crée autant d'ion I- qu'il n'en disparaît. Les ions iodures disparaissent en (1): lorsqu'un ion iodure réagit avec une molécule D il se forme un ion Br-. (1) D + I- ---> E + Br- initial a b 0 0 en cours date t a-(b-x) = a-b+x x .... b-x t infini a-b+xoo=0 en défaut xoo = b-a = 0,25 Eoo a = 0,25 date t3 :à la première équivalence nI- initialement présent = n Ag+ versé soit cAgve= [I-]v0. 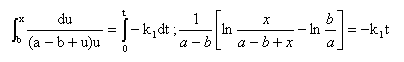[I-] = cAgve/v0 = 0,2*16/10 = 0,32 mol/L t(min) 0 5 10 20 40 80 infini x mol/L 0,5 0,422 0,375 0,32 0,277 0,255 0,25 La loi de vitesse d'une réaction SN2 s'écrit : -d[D]/dt = - d[I-]/dt = k1[D][I-] = k1(a-b+x) x dx/ ((a-b+x) x)= -k1t ; calcul de k1 à partir des données : t(min) 5 10 20 40 80 infini x mol/L 0,422 0,375 0,32 0,277 0,255 0,25 k1L mol-1 min-1 0,163 0,162 0,165 0,163 0,162 0,163 k1 moyen = 0,163 / 60 = 2,72 10-3 L mol-1 s-1

polarimétrie : détermination de k2.   On part d'un nouvel état initial, correspondant à l'état d'équilibre ontenu au bout d'un temps infini dans l'expérience précédente. Donner la composition du système dans cet état, soit les valeurs de [Br-]oo , [D]oo , [E]oo ,[E']oo en fonction de c= 0,125 mol/L. On modifie l'état précédent en doublant rapidement à t=0 la concentration de l'espèce E. On suit la réaction en étudiant le pouvoir rotatoire a de la solution en fonction du temps. On obtient les résultats suivants : t(s) 0 50 150 250 a (°) 1,3 0,9 0,45 0,2 Le pouvoir rotatoire a de la solution est donné par la formule : a = l S[a]i ci où l est la longueur de la cuve où l'on mesure a, [a]i est le pouvoir rotatoire spécifique de la substance dissoute n°i et ci sa concentration. On note a le pouvoir rotatoire spécifique de l'espèce E. On rappelle que celui de E' lui est opposé [a]' = -[a]. - Exprimer a à tout instant en fonction de [a], l, [E] et [E']. - Les seules réactions mises en jeu ici sont (2) et (2'). Quelle est la valeur de a lorsque t tend vers l'infini ? Que peut-o dire de [I-] au cours de la même réaction ? - A l'instant t quelconque, on note y la concentration dont a diminué [E] depuis l'instant initial. Exprimer [E] et [E'] en fonction de c et y. - Exprimer la vitesse d'apparition de E' en fonction de k2, [I-], [E] et [E']. En déduire une équation différentielle vérifiée par a, l'intégrer et donner a en fonction de a 0 ( valeur initiale de a à t=0) , k2, c et t. - Grâce au tableau, déterminer la valeur de k2 par une méthode non graphique ( tableau de valeurs demandé). - Comparer k1 et k2. ce résultat était-il prévisible ? Justifier. corrigé D est le réactif limitant Doo = 0 ; [I-]oo = 0,25 mol/L = 2c ; [Br-]oo = 0,25 mol/L = 2c ; les concentrations n'évoluant plus : d[E']/dt = 0 = k2[E]oo[I-]oo -k'2[E']oo[I-]oo ; avec k2=k'2 donc [E]oo= [E']oo. conservation de la matière : [D]+[E]+[E']=a soit 2[E]oo= a ; [E]oo=½a = c à chaque instant le pouvoir rotatoire s'écrit : a = l[a][E]+l[-a][E'] = l[a] ([E]-[E'] ) lorsque t -->oo le pouvoir rotatoire s'annule. la concentration [I-] reste constante, égale à 2c. à une date t, on note y la diminution de (E] depuis la date initiale. (2) E + I- ---> E' + I- initial 2c 2c c 2c en cours date t 2c-y 2c c+y 2c t infini Eoo 2c E'oo 2c a = l[a] ([E]-[E'] ) = l[a] (c-2y) ; da/dt = -2 l[a] dy/dt--> dy/dt= 1/(-2 l[a]) da/dt d[E']/dt =dy/dt = k2[E][I-] -k2[E'][I-]= k2[I-] ([E]-[E'] ) = 2c k2(c-2y) dy/dt =2c k2(c-2y) 1/(-2 l[a]) da/dt = 2c k2a /( l[a]) ; da/dt = - 4c k2a. ou da/ a = -4c k2 dt puis intégrer ln (a/a0)= - 4c k2 t on calcul k2 à partir du tableau de données : t(s) 50 150 250 a (°) 0,9 0,45 0,2 k2 L mol-1 s-1 0,0147 0,0141 0,0150 k2 moyen = 1,5 10-2 L mol-1 s-1 La constante de vitesse k1 est 7 fois plus petite que k2 : I- est meilleur nucléofuge que Br-, la liaison C-I ( plus longue que C-Br) est plus polarisable que la liaison C-Br. retour - menu