En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
| .
. |
| .
. |
- Deux tensions : a(t)=1,414 A cos(2pfat)
et e0 (t)= 1,414 E0 cos
(2pf0t+j0)
avec fa = 1420 Hz et f0 = 1450 Hz.
sont appliquées aux entrées d'un
multiplieur. La tension de sortie est : m(t)= a(t)
e0(t).
- Montrer que m(t) est la superposition de deux signaux sinusoïdaux de fréquence f et f '<f :
m(t) = M[cos (2pft+j0) + cos (2pf 't+j0)].
- Calculer f et f '. - Filtre
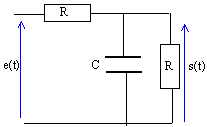
- Quel est le type de filtre ?
- Déterminer sa fonction de transfert H(x) en fonction de x= wRC.
- Déterminer sa pulsation de coupure w C en fonction de R et C.
- Le diagramme de Bode en gain de ce filtre est représenté ci-dessous. Donner une valeur approchée du produit RC.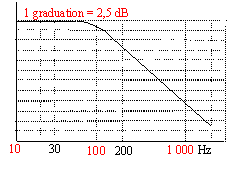
- En haute fréquence, quelle est la propriété du filtre ? Que devient le déphasage de s(t) par rapport à e(t) ?
- A l'entrée de ce filtre on injecte le signal
m(t). La tension de sortie sortie est :
s(t) = Scos (2pft+jS) +S' cos (2pf 't+jS')]
- Calculer S/S' à partir du diagramme de Bode.
corrigé
rappel mathématique : cos(a) cos(b) = ½[cos (a+b) + cos (a-b)]
a = 2pf0t+j0 et b= 2pfat ; a+b = 2p(f0+fa)t +j0 ; a-b = 2p(f0-fa)t +j0 ;
m(t) = AE0[cos (2p(f0+fa)t +j0) + cos (2p(f0-fa)t +j0 )]
soit f = f0+fa = 1420+1450=2870 Hz et f ' = f0-fa= 1450-1420= 30 Hz.
filtrage :
à basse fréquence le condensateur se comporte comme un interrupteur ouvert ; à haute fréquence il se comporte comme un court-circuit.
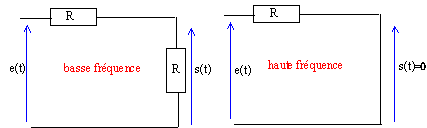
Les schémas équivalents montrent que ce filtre est un passe bas.
La fonction de transfert s'écrit : H(t) = S / E
admittance équivalente à R et C en dérivation : Y= 1 / R + jCw = [1 +jRCw] / R
et l'impédance est Z = 1/ Y = R / [1 +jRCw]= R / [1 +jx]
montage équivalent : 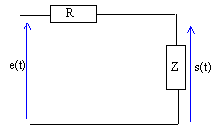
H(x) = Z / (R+Z) avec R+Z = R+R / [1 +jx] = R(2+jx) / (1+jx)
H(x) = 1 / (2+jx)= (2+jx)-1.
le gain du filtre est maximal à fréquence nulle ( x=0) : H = (4+x²)-½. Hmax = ½.
La pulsation de coupure à - 3 dB est telle que H(wC) = Hmax / 2½ soit x2 = 4 et RCwC= 2.
La fréquence de coupure sur le graphe vaut environ 150 Hz : d'où wC = 2*3,14*150 = 942 rads-1
et RC = 2/942 = 2,1 10-3 s.
En haute fréquence, la fonction de transfert s'écrit ( jx >> 2) : H(w) = 1 / (jRC w)
en conséquence le signal de sortie est l'intégrale du signal d'entrée. Sur le diagramme de Bode en gain on observe une pente de -20 dB par décade.
Si le signal d'entrée est sinusoïdal, le signal de sortie présente un retard de ½p.
mélangeur :
Le filtre est linéaire : le signal de sortie est obtenu en ajoutant les réponses aux deux composantes du signal d'entrée qui de plus ont la même amplitude. Le rapport des amplitudes de sortie est donc S/ S' = H(f) / H(f ')
lecture du gain en dB sur le diagramme de Bode
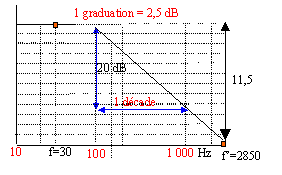
GdB = 20 log H soit log(S / S') = [(GdB(f)-GdB(f' )]/ 20= 11,5*2,5 / 20 = 1,43.
S/S' = 101,43 = 27; le filtre ne laisse donc passer que la composante basse fréquence du signal.
retour - menu