![]() Fluide
de Van der Waals d'après
Mines 99
Fluide
de Van der Waals d'après
Mines 99
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
| .
. |
| .
. |
Au sein des noyaux lourds la matière nucléaire ( protons et neutrons) se comporte comme un fluide de Van der Waals ( modèle très simple). L'équation d'état d'une mole de ce fluide est (P+a/V²)(V-b)=RT. a et b sont deux constantes caractéristiques du fluide étudié. a=122 ; b=10-4 S.I . P: pression ; V: volume ; T : température.
L'énergie interne d'une mole de fluide est : U(T,V) =CvT-a/V ; Cv : capacité calorifique molaire à volume constant du fluide ; Cv est considérée comme une constante.
- Déterminer les unités de a et b dans le
S.I.
- Quelle est l'interprétation physique de a et b ?
- On assimile les particules du fluide à des sphères de rayon r. Donner l'ordre de grandeur de r. NA= 6,02 1023 mol-1. - Montrer que l'entropie d'une mole de fluide S(T,V) = Cv lnT+ Rln(V-b) + Cte.
- On réalise une transformation adiabatique
réversible conduisant une mole du fluide de
l'état (T0=300K ; V0= 0,02
m3 ) à l'état (T1 ;
2V0). Déterminer T1 en
fonction de T0, V0, b, R et
Cv.
- On mesure expérimentalement T1=230 K; en déduire Cv.
- Quelle est à priori la structure moléculaire des particules du fluide étudié ?
- Déterminer le travail reçu par le fluide lors de cette transformation, en fonction de T1, T0, V0, a et Cv. Faire le calcul. -
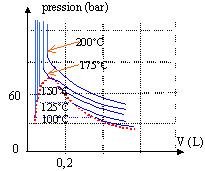
La figure ci-dessus donne un ensemble de courbes expérimentales, appelées isothermes d'Andrews ( pour une mole de fluide).
- Comment s'appelle la courbe en pointillés rouges ?
- Déterminer les coordonnées du point critique C ; donner les propriétés physiques de ce point.
- Préciser l'état physique du fluide et calculer, après les avoir définis, les titres molaires xv et xl de la vapeur et du liquide dans les trois cas suivants :
* le fluide occupe un volume égal à 0,6 L à 110°C.
* le fluide est placé sous une pression de 110 bars à 200°C
* le fluide occupe un volume de 0,2 L à 125 °C.
- Que vaut le volume molaire de la vapeur saturante sèche à la pression de 40 bar ?
corrigé
unité de b : volume en m3 ;
a/V² a la dimension d'une pression ; a a la dimension de PV² soit PV * V ;
PV a la dimension d'une énergie en joule ; unité de a : Jm3 .
a/V² : pression moléculaire ; l'effet attractif entre molécules diminue la pression sur les parois.
b représente le volume propre des NA molécules ( dans une mole) assimilées à des sphères de rayon r. L'ordre de grandeur de r est :
volume d'une sphère = 4/3pr3 ; NA= 6,02 1023 molécules dans une mole
b = 4/3pr3 NA soit r3 = 3b/(4pNA)
r3 = 3*0,25 / (4*3,14 *6,02 1023 ) = 9,92 10-26 soit r =4,6 10-9 m
r est de l'ordre de grandeur du rayon de l'atome
entropie :
L'énergie interne d'une mole de fluide est : U(T,V) =CvT-a/V ;
calcul de la différentielle dU : dU= CvdT +a/V² dV
La variation d'énergie interne est la somme de la chaleur et du travail reçus par le système.
travail élémentaire et chaleur reçus lors d'une transformation élémentaire réversible :
dW= -PdV ; dQ= TdS
d'où dU= -PdV + TdS = CvdT +a/V² dV
TdS= CvdT+( P+a/V² )dV
or (P+a/V²)= RT / (V-b) d'où TdS= CvdT+RT / (V-b) dV
dS= Cv/T dT + R / (V-b) dV
par intégration on trouve l'entropie S(T,V) = Cv lnT+ Rln(V-b) + Cte.
détente adiabatique réversible :
La détente est adiabatique et réversible, donc isentropique.
S(T1,2V0) =S(T0,V0)
soit : Cv lnT0+ Rln(V0-b) =Cv lnT1+ Rln(2V0-b)
lnT1= lnT0+R/Cv ln[(V0-b)/(2V0-b)]
Cv =R[ln(V0-b)-ln(2V0-b)] / [lnT1- lnT0]
Cv =R[ln((V0-b)/(2V0-b))] / [ln(T1/T0]
Cv = 8,314 [ln((0,02-10-4) /(0,04-10-4))] / [ln(230/300)]=8,314*(-0,696) / (-0,266)=21,74 J K-1mol-1.
Cv est voisin de 2,5 R, le gaz est probablement diatomique.
travail reçu par le fluide :
dans une détente adiabatique le travail reçu est égal à la variation d'énergie interne du fluide.
W=DU = U1-U0 avec U= CvT-a/V ;
DU =Cv(T1-T0)-a[1/(2V0)-1/V0]=Cv(T1-T0)+a/(2V0)
DU = 21,74*(230-300)+122/0,04 = -1521,8 +3050=1528,2 J.
équilibre liquide vapeur :
La courbe en pointillé est la courbe de saturation. Son sommet est le point critique C. La branche gauche est la courbe d'ébullition ( apparition des premières bulles de vapeur) et la branche droite, la courbe de rosée ( apparition des premières gouttes de liquide)
PC voisin 80 bar et VC voisin 0,1 L.
Au dessous de la température critique 175 °C, l'état vapeur et l'état liquide sont distincts; à l'équilibre les deux phases sont séparées par un ménisque. Au dessus de 175°C, le liquide et la vapeur forme une phase unique, fluide hypercritique.
A : 0,06 L ; 110°C état vapeur
B : 110 bar ; 200°C état hypercritique
D : 0,2 L ; 125°C mélange liquide vapeur
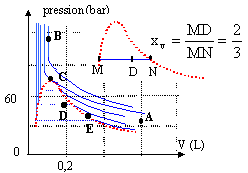
fraction molaire de la vapeur : xv=0,66 ; du liquide : xl=0,34
E 40 bar ; V = 0,35 L
retour - menu