doublet de lentilles minces ; oculaires

Aurélie 01/02

vision d'un petit objet à l'aide d'un microscope

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

On considère un microscope optique, fonctionnant en lumière blanche, dont l'objectif et l'oculaire sont assimilés à deux lentilles minces convergentes L₁ et L₂ de focale image f₁ = 2 mm et f₂ = 30 mm. L'ensemble est dans l'air. L'oeil est placé en O au voisinage du foyer image de l'oculaire F_{i 2}. Il observe l'image définitive située à la distance minimale de vision distincte d_m =25 cm de O.

L'intervalle optique D séparant le foyer image F_{i 1}de L₁ du foyer objet F_{0 2}de L₂ est égal à 180 mm. On fera les approximations utiles sachant que f₁ <<f₂ <<D.

Les grandeurs écrites en bleu et en gras sont algébriques.

L'oeil se trouve au centre du cercle oculaire, image de la monture de L₁ donnée par L₂. Trouver F_{i
2}O en fonction de f₂ et D et calculer sa valeur.
- En déduire le diamètre a du cercle oculaire sachant que la monture de L₁ a un diamètre D =11 mm.
Trouver le grandissement du microscope en fonction de f₂, f₁, d_met D. Calculer sa valeur.
Du fait de la structure granulaire de la rétine, l'oeil ne peut distinguer deux points que si l'angle sous lequel il les voit est au moins égale à e = 1,5 minutes d'angle. Trouver en fonction de f₂, f₁, e et D la taille l du plus petit objet donts les extrémités A et B sont vues distinctement à travers le microscope.
- Calculer l et comparer sa valeur à la longueur d'onde moyene de la lumière blanche utilisée. Conclure.

corrigé

cercle oculaire :

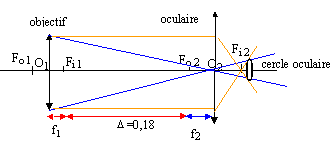
formule de Newton appliquées à L₂ :

l'objet est la lentille L₁ de centre optique O₁.

F_{o
2}O₁ * F_{i 2}O= - f₂²

or F_{o
2}O₁ = F_{o 2}F_{i
1} + F_{i 1}O₁= -D -f₁ voisin de -D .

F_{i 2}Ovoisin f₂² / D = 0,03 ² / 0,18 = 5 10^-3 m .

en utilisant les triangles semblables :

a / D = O₂O / O₁O₂ avec O₁O₂ = f₁ + D + f₂ voisin D et O₂O voisin f₂.

a voisin f₂D /D = 0,03 *0,011 / 0,18 = 1,8 10^-3 m.

grandissement du microscope :

grandissement transversal du microscope : G_t = A_iB_i / A_oB_o = A_iB_i / A₁B₁*A₁B₁ / A_oB_o

pour l'objectif : G_{t
1} = A₁B₁ / A_oB_o= - F_{i
1}A₁/ f₁

F_{i
1}A₁= F_{i 1}F_{o
2} + F_{o 2}A₁= D + F_{o 2}A₁ .(1)

formule de Newton : F_{o 2}A₁ *F_{i 2}A_i = -f₂².(2)

F_{i 2}A_i = F_{i
2}O + OA_i= F_{i
2}O -d_m voisin de -d_m .

(2) s'écrit : F_{o 2}A₁= f₂²/ d_m.

(1) s'écrit : F_{i
1}A₁= D + f₂²/ d_m.

G_{t 1} = -( D + f₂²/ d_m) / f₁ = -(0,18 + 0,03² / 0,25) / 2 10^-3 = -91,8.

pour l'oculaire : G_{t
2} = A_iB_i /A₁B₁= - F_{i
2}A_i/ f₂= f₂/F_{o
2}A₁

(2) conduit à G_{t 2} = d_m/ f₂= 0,25 / 0,03 = 8,33.

pour le microscope G_t = G_{t 1} * G_{t 2} = -( D + f₂²/ d_m) / f₁ *d_m/ f₂voisin de - D d_m/ (f₁f₂)

G_t = -91,8*8,33 = -765.

limite de résolution :

diamètre apparent ou angle sous lequel l'observateur voit l'objet à travers le microscope : A_iB_i/ d_m.

ce diamètre apparent doit être supérieur ou égal à e.( 1,5 / 60 = 0,025 ° soit 0,025*3,14/180 = 4,3 10^-4 rad)

A_iB_i/ d_m>= e.

grandissement du microscope |G_t| = A_iB_i / A_oB_o d'où A_iB_i= |G_t| A_oB_o

|G_t| A_oB_o/ d_m>= e.

A_oB_o>= e d_m/ |G_t| avec |G_t| = D d_m/ (f₁f₂)

A_oB_o>= e f₁f₂/ D soit A_oB_o>=4,3 10^-4 * 0,03 * 2 10^-3 / 0,18 = 1,4 10^-7 m = 0,147 mm.

cette valeur est inférieure à la longueur d'onde moyenne de la lumière blanche (de l'ordre de 0,5 mm ) :

c'est donc la diffraction qui limite la taille du plus petit objet visible par l'instrument et non pas le pouvoir séparateur de l'oeil.

retour - menu