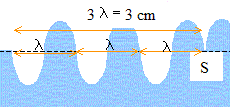En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||
|
||||||||
|
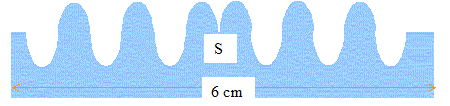
C'est une vague qui remonte certain fleuve à marée montante. On donne sa célérité v = 25 km/h soit 25/3,6 = 6,94 m/s. On donne une coupe de la surface de l'eau à la date t=0. 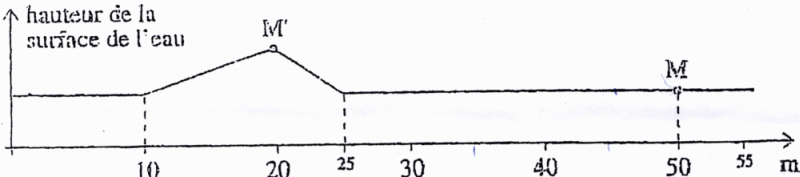 Le mascaret est une onde transversale : la direction de propagation est horizontale, tandis que la déformation de l'eau s'effectue suivant la verticale. A t = 5,04 s, quelle sera la perturbation au point M ? En 5,04 s, la vague parcourt : 5,04*6,94 ~ 35 m ; or le point M est situé à 50 m, ce dernier n'est pas encore atteint par la vague. M ne subit aucune perturbation à cette date. Â l'instant t =5,04 s, quel point N subit la même perturbation que le point M' à la date t=0 ? La perturbation parcourt 35 m en 5,04 s ; M' est situé à l'abscisse 20 m. N se trouve donc à l'abscisse 20+35 = 55 m. Donner l'allure de la surface de l'eau à t = 5,04 s.  Onde progressive sinusoïdale à la surface de l'eau. Texte : fréquence f= 50 Hz. A la date t on donne une coupe verticale de la surface de l'eau .
Quel est la valeur de t ? ( 6 ms ; 30 ms ; 60 ms ; 90 ms ; 120 ms) Analyse : Question relative à date de la prise de vue. L'onde se propage dans toutes les directions à partir de la source S.
d'où t = 3T = 0,06 s =
60
ms.
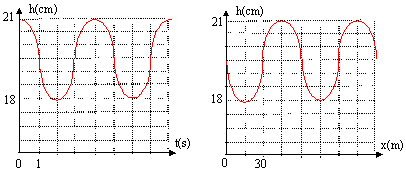
La houle. Texte : Dans l'approximation de la houle ( vague d'amplitude très inférieure à la longueur d'onde) en eau profonde, la célérité de la houle s'exprime par la relation c = [gl/(2p)]½, dans laquelle g est l'accélération de la pesanteur et l la longueur d'onde de la houle. g= p 2 = 10. Analyse : Question relative à la nature de l'onde. La perturbation est perpendiculaire à la direction de propagation : onde transversale. Question relative à "le milieu est-il dispesif". l = c/f et c2 =gl/(2p) d'où c2 = gc/(2pf) ; c = g/(2pf) La célérité dépend de la fréquence de l'onde : le milieu est donc dispersif. Question relative à la célérité, la fréquence étant connue ( 3,14 Hz). c= g/(2pf) = 10/(2p2) = 1/2 = 0,5 m/s.
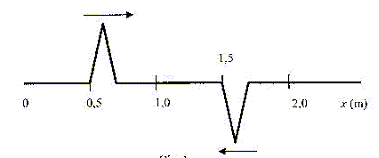
Ondes sur une corde. Texte : deux ondes se propagent dans la même direction et en sens contraire sur une corde. La valeur commune de la célérité des deux ondes est v= 5,0 m/s. A l'instant t=0 la corde à l'aspect suivant :
Analyse : Question relative à l'allure de la corde à t = 0,1 s. En 0,1 s chaque perturbation parcourt 0,1*5 = 0,5 m. La corde a l'aspect suivant : (pas de déformation de la corde)
|
||||||||
|
|
||||||||
|
|