Concours kiné berck : 9 années de QCM Laser, photons, réfraction, diffraction, ondes. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

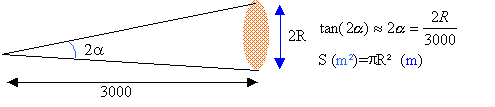
Une source laser est supposée ponctuelle. Le faisceau émis est légèrement divergent, assimilable à un cône de demi angle au sommet a=0,5 10-4 rad. Quelle est la surface de la tache lumineuse produite par le laser sur la façade d'un immeuble situé à 3 km (en m²) ? R= 3000*0,5 10-4 = 0,15 m ; S= 3,14*0,152 =0,071 m2. Une lampe spectrale émet un rayonnement de longueur d'onde l=366 nm. La quantité de photons émis par heure est N= 332 mmol /h. Données : h= 6,62 10-34 Js ; c= 3 108 m/s ; nombre d'Avogadro 6,02 1023 mol-1. Déterminer la puissance (en W) avec laquelle la lampe émet ce rayonnement (5,2 ; 16,4 ; 30,1 ; 32,3 ; 38,1 ; aucune réponse exacte) énergie d'un photon : E=hc/l= 6,62 10-34*3 108 / 366 10-9 = 5,43 10-19 J nombre de photons émis par seconde : 0,332*6,02 1023 /3600 = 5,55 1019 photons énergie libérée en une seconde : 5,55 1019* 5,43 10-19 = 30,1 W L'indice d'un verre, pour une radiation de longueur d'onde l se calcule par la formule de Cauchy : où A et B sont des constantes. Pour la lumière rouge : l R= 775 nm ; indice nR= 1,617. Pour la lumière violette : l V= 427 nm ; indice nR= 1,642. Calculer l'indice du verre pour une radiation jaune l J= 579 nm. c1,617 = A + B/(775 10-9)² =A + 1,665 1012 B.(1) 1,642 = A + B/(427 10-9)² =A + 5,485 1012 B.(2) (2)-(1) donne : 0,025 = 3,82 1012 B ; B= 6,545 10-15 m-2. d'où A = 1,606. nJ= 1,606 + 6,545 10-15 / (579 10-9)²=1,626.   La lumière d'un laser est diffactée par une fente de largeur a. On observe la figure de fiffraction sur un écran à la distance D de la fente. La tache centrale a pour largeur L. La longueur d'onde du faisceau laser est l = 0,6328 mm. D= 2,5 m ; a= 0,2 mm. Calculer la largeur L (cm) de la tache de diffraction. L= 2*0,6328 10-6 * 2,5 / 2 10-4 = 1,58 10-2 m voisin 1,6 cm.     Web www.chimix.com Une corde est tendue par le poids d'une masse m= 200 g; OB= 250 cm ; AP= 150 cm. On montre que la célérité des ondes transversales le long d'une corde est donnée par la relation v=( F/m)½ avec F tension de la corde en N et m masse par unité de longueur de corde. On produit une brève secousse à l'extrémité O de la corde. On déclenche le chronomètre lorsque la perturbation arrive au point A de la corde. On arrête le chronomètre lorsque la perturbation arrive au point P et on lit Dt= 0,35 s. Déterminer la masse ( en kg ) de la corde.(0,18 ; 0,27 ; 0,35 ; 0,56 ; 0,84 ; aucune réponse) AP= 1,5 m ; Dt= 0,35 s ; v = AP/Dt=1,5/0,35 = 4,286 m/s F= mg = 0,2*9,8 = 1,96 N m = F/v² = 1,96 / 4,289² = 0,107 kg /m masse de la corde : 0,107*2,5 = 0,27 kg. Un coup sec est appliqué à une canalisation en acier dans laquelle circule du pétrole. Un capteur situé à la distance d=480 m du point d'application du coup, enregistre deux signaux sonores très brefs séparés par une durée Dt= 224 ms. Vitesse de propagation du son dans l'acier va= 5,00 km/s. Déterminer la vitesse ( en km/s) de propagation du son dans le pétrole. (0,85 ; 1,20 ; 1,50 ; 1,70 ; 2,10 ; aucune bonne réponse) durée du parcours dans l'acier : ta = d/ va= 0,48 / 5 = 0,096 s durée du parcours dans le pétrole : tp= d/vp = 0,48 / vp Dt=tp-ta ; 0,224 = 0,48 / vp-0,096 ; 0,32 = 0,48 / vp ; vp= 0,48/0,32 =1,5 km/s. 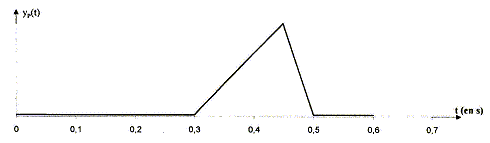Une perturbation transversale se propage le long d'une corde tendue horizontalement. La déformation commence à l'instant t=0 en un point S. On considère un point P situé à la distance x=3,6 m du point S. Le mouvement de P est un mouvement rectiligne vertical suivant l'axe des y. On note yP(t) la représentation de la position de P en fonction du temps. Calculer la célérité ( m/s) de la perturbation le long de la corde.(7,2 ; 12 ; 18 ; 24 ; 30 ; aucunne réponse exacte) La perturbation atteint le point P, situé à une distance d= 3,6 m de la source avec un retard de 0,3 s ; d'où la célérité : 3,6 / 0,3 = 12 m/s. Les niveaux d'énergie de l'atome d'hydrogène ont pour valeur En=-13,6 / n2 (eV). h= 6,63 10-34 J s ; 1 eV= 1,6 10-19 J ; c= 3,00 108 m/s. Parmi les affirmations suivantes combien il y en a-t-il d'exactes ? - Le spectre d'émission de l'atome d'hydrogène est continu. faux. - L'énergie minimale d'un électron capable de provoquer l'excitation d'un atome d'hydrogène à partir de son niveau fondamental vaut 10,2 eV.vrai. La différence dénergie entre le premier niveau excité et le niveau fondamental vaut 13,6-13,6/4 = 10,2 eV. Le choc entre l'atome d'hydrogène et un électron d'énergie 10,2 eV conduit à l'excitation de l'atome. - L'atome d'hydrogène peut émettre la radiation de longueur d'onde dans le vide l=122 nm en passant du niveau d'énergie n=2 au niveau n=1.vrai. DE= 10,2 eV soit 10,2*1,6 10-19= 1,63 10-18 J DE= hc/ l ; l=hc/DE= 6,63 10-34*3 108/1,63 10-18 =1,22 10-7 m = 122 nm. - Le niveau d'énergie 0 eV correspond à l'atome d'hydrogène dans son niveau fondamental.faux. niveau fondamental : n=1 et E=-13,6 eV ; atome ionisé E=0 eV. - La valeur de l'énergie de l'atome d'hydrogène au niveau n=4 est de -1,36 10-19 J.vrai. E4 = -13,6 / 16=-0,85 eV soit -0,85*1,6 10-19 = -1,36 10-19 J. 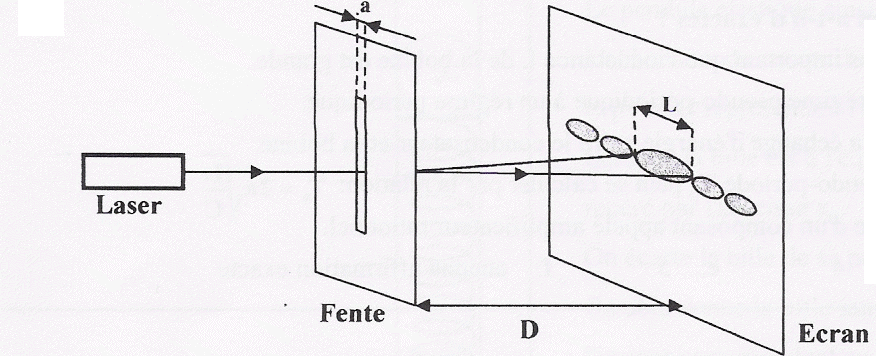Texte : une pointe vibrant à la fréquence f=80 Hz produit des rides circulaires à la surface de l'eau d'une cuve à onde. La célérité de l'onde vaut 24 cm/s. Analyse : Question relative à la distance ( cm) séparant la 1ère et la 10è crête. (2,7 ; 3,0 ; 3,3 ; 3,0 ; 6,6 ; aucune réponse exacte) Un point de la 1ère crête et un point de la 10è crête vibrent en phase. Ils sont distants d'un nombre entier de longueur d'onde l. La distance dans ce cas vaut 9 l.  Or l = c/f ; l = 24 / 80 = 0,3 cm. puis 9*0,3 = 2,7 cm. Texte : la célérité du son dans l'air se calcule par la relation : c = [gP/m]½. g = 1,4 pour l'air ; P : pression de l'air ( Pa) ; m : masse volumique de l'air ( kg m-3). Mair = 29,0 g/mol ; R = 8,31 J K-1 mol-1. Analyse : Question relative à la célérité du son(m/s)dans l'air à -17°C. (308 ; 319 ; 327 ; 331 ; 340 ; aucune réponse exacte) Equation des gaz parfaits : PV=nRT avec n = m/Mair ; PV = m/MairRT Or m/V = m ; P = mRT/Mair ; P/m = RT/Mair avec T = 273-17 = 256 K et Mair = 0,029 kg/mol. c = [gP/m]½ = [gRT/Mair]½. c = [1,4*8,31*256/0,029]½ =320 m/s.

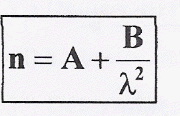retour -menu