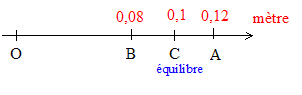|
Concours Esiee : 4 années de QCM pendule, oscillateur élastique En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||
|
||||||||||
T = 2p [L/g]½. B- La période du mouvement est proportionnelle à L. Faux. "proportionnelle à L½" . C- La vitesse maximale atteinte est indépendante de m. Vrai. th de l'énergie cinétique entre A et M : DEc=½mv2 - 0 La tension du fil perpendiculaire à la vitesse ne travaille pas. travail du poids ( de A vers M) ; origine des altitudes : la position d'équilibre) W = mgL(cosq- cos qA). ½mv2 = mgL(cosq- cos qA) ; v2 =2gL(cosq- cos qA) D- La tension du fil est de norme constante au cours du mouvement. Faux. E- La fréquence
du mouvement est indépendante de
m.
Vrai. La fréquence est l'inverse de la
période ; la période est
indépendante de m.
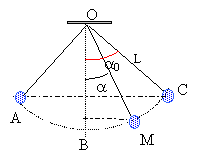
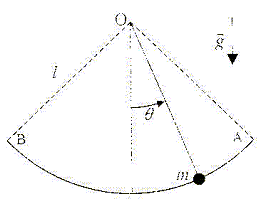
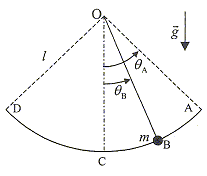
Une masse m attachée à un fil inextensible,
sans masse, de longueur L, oscille dans un plan vertical
entre les positions A et C. g= 10 m/s² période T=
2p(L/g)½
= 2 s soit L=T²g/(4p²)
= 4*10 / 40 = 1 m b) vrai ; a)
faux. L'accélération de m est normale à la trajectoire si le mouvement est circulaire uniforme ; ce qui n'est pas le cas ici. c) faux.
Le régime est pseudopériodique ( amortissement) d) faux
Une masse m=25 g est attachée à l'extrémité d'un ressort horizontal, de constante de raideur k= 0,2 N/m et de longueur à vide Lo= 10 cm. L'autre extrémité du ressort est fixée à un point fixe O. A est le point d'abscisse OA = 12 cm et B est le point d'abscisse OB= 8 cm. On lâche m de A avec une vitesse nulle. Cette masse se déplace sans frottement sur le plan horizontal selon l'axe Ox.
L'énergie potentielle élastique de m en A vaut-elle 0,04 mJ ? vrai. En A la déformation du ressort vaut : |longueur - longueur initiale| = L-L0 = x Energie potentielle élastique en A : Ep(A) = ½kx² = 0,5*0,2 (0,02)² = 4 10^ - 5 J = 0,04 mJ. L'énergie potentielle élastique de m en B vaut-elle 0,64 mJ ? faux. En B la déformation du ressort vaut : longueur - longueur initiale = x=0,02 m La déformation en B est identique à la déformation en A : donc l'énergie potentielle élastique en B est à l'énergie potentielle élastique en A. La pulsation du mouvement vaut-elle 8 rad/s ? faux. w2 = k/m ; raideur k(N/m) et masse m (kg) ; w2 = 0,2 / 0,025 = 8 ; w = 8½ rad/s. L'énergie cinétique de m lorsque m est au milieu de [AB] vaut-elle 0,04 mJ ? vrai. En C, milieu de [AB], le ressort n'est pas déformé : l'énergie mécanique du système {masse + ressort} est sous forme : ½mv² En B, m est immobile : l'énergie mécanique du système {masse + ressort} est sous forme : ½kx² ( avec x= 0,02 m) L'énergie mécanique se conserve( frottements négligés) Energie cinétique en C = énergie potentielle élastique en A= 0,04 mJ. L'énergie mécanique de m en A vaut-elle 1,44 mJ ? faux. Energie cinétique en C = énergie potentielle élastique en A= énergie mécanique= 0,04 mJ.
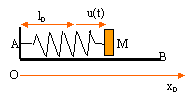
Une plate forme AB a un mouvement périodique de
période T, parallèlement à
Ox0 fixe par rapport à un observateur
terrestre. On installe à bord de cette plate forme un
système comportant un ressort de raideur k. L'une des
extrémités est solidaire d'une masse M
assimilable à un point matériel et l'autre
extrémité est fixée en A. On note u(t)
l'abscisse de M par rapport à la plate forme.
L'origine de u est la position d'équilibre de la
masse. La masse M subit une force de frottement
F=-fv
colinéaire à sa vitesse par rapport à
la plate forme.
période propre du résonateur ( ressort + M)
:T0 = 2p(M/k)½.
d) Une résonance aigue correspond nécessairement à une fréquence de résonance élevée. e) La résonance est d'autant plus floue que f est élevé. Une résonance aigue correspond à un amortissement faible. La résonance floue correspond à un amortissement fort d) faux ; e) faux. |
||||||||||
|
|
||||||||||
|
|
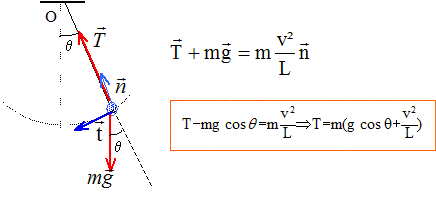
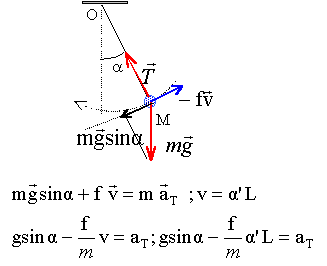 e)
faux
e)
faux