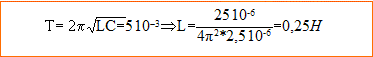Concours Esiee : 4 années de QCM condensateur, dipôle RC En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

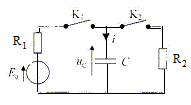
Le condensateur est initialement déchargé. Le générateur délivre une tension E0. Les résistances R1 et R2 sont différentes. De t=0 à T K1 est fermé et K2 est ouvert. T est suffisamment long pour charger complètement le condensateur. A- L'intensité initiale du courant est nulle. Faux. additivité des tensions à la date t=0 : E0 = R1 i(0) + uC (0) ; or uC(0) = 0 d'où i(0) = E0/R1. B- La tension finale aux bornes du condensateur est nulle. Faux. La tension finale aux bornes du condensateur vaut E0. A partir de t=T, K1 est ouvert et K2 est fermé. C- L'intensité initiale lors de la décharge est nulle. Faux. Le courant change de sens. additivité des tensions à la date t=T+ : 0= R2i(T+) + uC (T+) ; or uC(T+) = E0 d'où i(T+) = -E0/R2. D- La tension uC à la date t =T+ vaut -E0. Faux. Continuité de la tension aux bornes du condensateur uC(T+) =uC(T-) = E0 E- La constante de temps du circuit entre [0 ; T) est la même qu'à t >T . Faux. t1 = R1C et t2 = R2C avec R1différent de R2.   Le condensateur est initialement déchargé. Le générateur délivre une tension E0 = 4 V. C= 10 mF ; R1 =10 W et R2 =20 W. De t=0 à T =1 ms K1 est fermé et K2 est ouvert. T est suffisamment long pour charger complètement le condensateur. A- Lénergie accumulée dans le condensateur à t=T vaut 8 10-5 J. Vrai. Le condensateur est chargé ; la tension à ses bornes vaut E0=4 V. ½CE02 = 0,5*10-5*16 = 8 10-5 J B- L'énergie dissipée par effet joule de t=0 à T à travers R1 vaut 8 10-5 J. Vrai. Energie dissipée par effet Joule dans R1 pendant la durée dt : dW =R1i2dt avec i = E0/R1 exp(-t/t) ; t = R1C = 10-4 s ; T= 10t. dW= R1(E0/R1)2exp(-2t/t)dt intégrer entre 0 et 10t : E02/R1 (-½ t )[exp(-2t/t)]010t =E02/R1 (½ t ) = 16/10 * 5 10-5 = 8 10-5 J C-L'énergie fournie par le générateur de t=0 à t=T vaut 8 10-5 J. Faux. L'énergie fournie par le générateur est égale à la somme de l'énergie stockée par le condensateur et de l'énergie dissipée par effet joule. soit 16 10-5 J. A partir de t=T, K1 est ouvert et K2 est fermé. D- L'énergie accumulée par le condensateur à t=T vaut 16 10-5 J. Faux. 8 10-5 J E- L'énergie dissipée par effet joule à travers R2 vaut 16 10-5 J. Faux. Elle est égale à l'énergie stockée initialement par le condensateur soit 8 10-5 J.     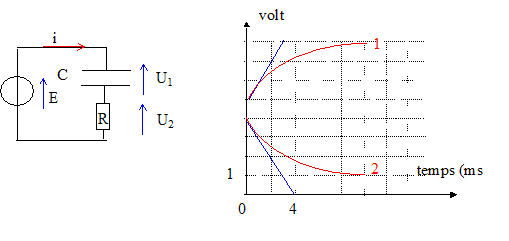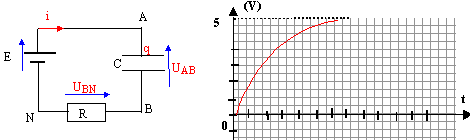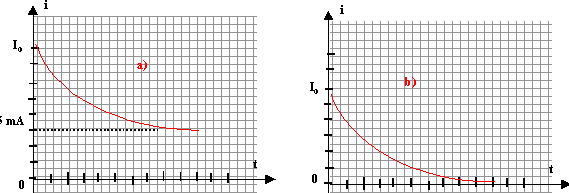Web www.chimix.com On considére le montage série ci-dessous R= 300 ohms. A l'instant t=0, on ferme le circuit, le condensateur étant initialement déchargé. 1. La courbe 1 correspond-elle à la tension aux bornes du résistor ? faux. Courbe 1 : la tension aux bornes du condensateur est croissante lors de la charge. L'intensité du courant décroît de la valeur E/R à la valeur zéro lors de la charge. De plus la tension aux bornes d'un résistor et l'intensité qui le traverse sont proportionnelles. Courbe 2 : tension décroissante aux bornes du résistor, image de l'intensité. 2. E vaut-elle 3 V ? vrai. En fin de charge : - l'intensité du courant est et en conséquence la tension aux bornes du résistor sont nulles. - la tension aux bornes du condensateur est alors égale à la tension aux bornes du générateur. Le graphe indique U1 max = 3 V, donc E= 3 V La constante de temps t vaut-elle 4 ms ? L'abscisse de l'intersection de la tangente à l'origine avec l'asymptote horizontale donne la constante de temps t. Sur le graphe 1 ou lit : t = 1,5 divisions soit 3 ms. faux.  4. La valeur de la tension aux bornes du résistor à la date t= t vaut-elle 2 V ? faux. A t= t l'intensité, donc la tension aux bornes du résistor est égale à 37 % de sa valeur initiale ; soit environ 3*0,37 voisin 1 V. 5. La capacité du condensateur vaut-elle C= 5 microfarads ? faux. t = RC avec R= 300 ohms et t = 3 10-3 s C= t / R = 3 10-3 / 300 = 10-5 farad = 10microfarads. 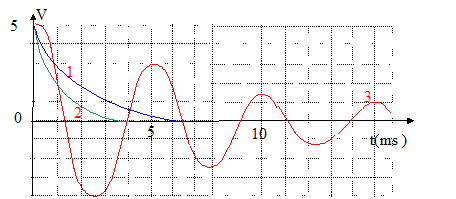Les courbes ci-dessous représentent l'évolution de la tension aux bornes du condensateur en série avec une résistance R variable et une inductance L fixée pendant une durée de 20 ms. Le condensateur porte une charge initiale de 12,5 microcoulombs. R peut prendre les valeurs suivantes (ohms) 50 ; 630 ; 1000.   1. La capacité vaut-elle C= 2,5 microfarads ? vrai. Q= CU Q : charge maxi en microcoulomb ; C : capacité en microfarad ; U: tension maximale (V) aux bornes du condensateur C= Q/U= 12,5 / 5 = 2,5 microfarads.  2. L'inductance vaut-elle L= 250 mH ? vrai.  3.Les trois courbes correspondent-elles à des régimes pseudo-périodiques ? non La courbe 3 correspond à un régime pseudo-périodique. Les autres courbes correspondent à un régime apériodique. 4. La courbe 1 correspond-elle à R = 1000 ohms ? non La courbe 2 correspond à la plus grande valeur de la résistance.  5. La courbe 3 correspond-elle à R= 630 ohms ? vrai. La courbe 2 correspond à la plus valeur de la résistance.   La tension aux bornes d'un condensateur de capacité C, en série avec une résistance R= 250 W, évolue en fonction du temps comme indiqué ci-dessous.L'énergie accumulée par le condensateur au bout d'un temps très long est de 1 mJ. Le courant i est de la forme : c) I0= 20 mA d) C= 0,4 mF e)C=80 m F a) faux ; b) vrai I0 = 5/ 250 = 0,02 A = 20 mA c) vrai énergie stockée par le condensateur en fin de charge : ½CU²= 10-3 J ; C= 10-3*2/U² =2 10-3 / 52 = 8 10-5 F = 80 m F e) vrai ; d) faux.

retour -menu