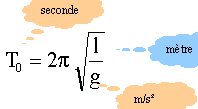En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||
|
||||||||||
|
Texte :
Analyse : Quelle est la variation relative ( %) de la période si la longueur varie de 2 % ? DT/T = 0,5 D L/L avec D L/L= 0,02 DT/T = 0,5*0,02 = 0,01 ou 1 %.
Texte : On s’intéresse à
l’énergie mécanique d’un
système ressort-masse horizontal. On négligera les frottements sur le plan
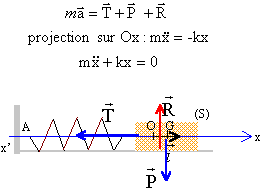
horizontal Analyse : L'équation
différentielle qui régit le mouvement
s'écrit : x"-k/m x=0.
Faux. L’équation
du mouvement est x(t) = A cos (
(k/m)½t+j).
Vrai. k/m représente
la période de ce mouvement en
rad.s-1.
Faux. période T : pulsation w0
(rad/s )telle que w0²=
k/m Au maximum de
l’élongation, l’énergie
mécanique est E =
½kA2.
Vrai. L'énergie cinétique est nulle ;
l'énergie mécanique est sous forme
potentielle élastique.
Pendule simple. Texte : On considère un pendule simple constitué d’une masse m=250 g attachée à un fil sans masse de longueur L=1 m. On négligera les frottements de l’air, on prendra g=10m.s-2 et 0,1½~0,314 ; p ~3,14 Analyse : La variation de q , angle par rapport à la normale, au cours du temps exprime parfaitement le mouvement de ce pendule. Vrai. La période du mouvement est d’environ 2 secondes. Vrai.
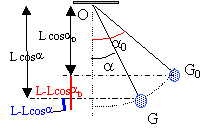
T0 = 2p (1/10)½ =2*3,14* 0,314 = 2 s. Le travail du poids du pendule pendant son mouvement est W= -mgL(1-sin q). Faux. le travail du poids est égal à : mg ( zG-zG0) l'origine des altitudes est prise au point le plus bas, la position d'équilibre.
mg ( zG0 -zG) = mg ( L-Lcosa0 -L+Lcosa) mg ( zG0 -zG ) = mgL(cosa -cosa0 ). L’énergie n’est pas conservée. Faux. En absence de frottement l'énergie mécanique est constante.
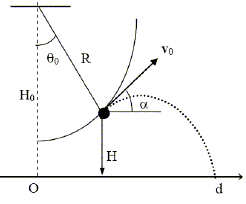
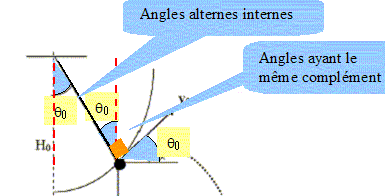
On considère un pendule simple, constitué d'une bille sphérique de masse ponctuelle m, suspendue parl'extrémité d'un fil inextensible de longueur R à un plafond horizontal.
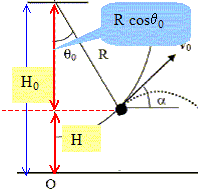
La masse m est libérée avec une vitesse v0. On prendra g=10 N/kg et Ep=0 pour H=0 (au niveau du sol). La hauteur H par rapport au sol quand le pendule est à l'angle q0 est H= H0-R cos q0. Vrai.
Si le pendule a une amplitude maximale qmax, la vitesse v0 au point q0<qmax est : [2gR(cosq0-cosqmax)]½. Vrai. Au point d'amplitude angulaire qmax, la vitesse est nulle. L'énergie du pendule est sous forme potentielle de pesanteur : EM = mg( H0-R cos qmax). Au point d'amplitude angulaire q0, la vitesse est v0. L'énergie du pendule est sous forme potentielle de pesanteur et cinétique : EM =mg( H0-R cos q0) + ½mv20. Ecrire la conservation de l'énergie mécanique , en l'absence de frottement : mg( H0-R cos qmax) = mg( H0-R cos q0) + ½mv20. -R gcos qmax= -Rg cos q0 + ½v20 ; v20 = 2gR(cosq0-cosqmax). La vitesse v0 fait un angle q0 par rapport à l’horizontale. Vrai.
L’énergie cinétique de la masse arrivée au sol est nulle. Faux.
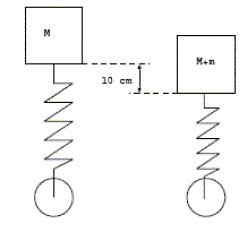
On considère une masse M posée sur un ressort qui se met à osciller avec une période de 1,5 secondes et est comprimé de 10 cm lorsque qu’on rajoute une masse m.
La période d’oscillation de la masse M à vide est plus courte qu’en présence de la masse m. Vrai.
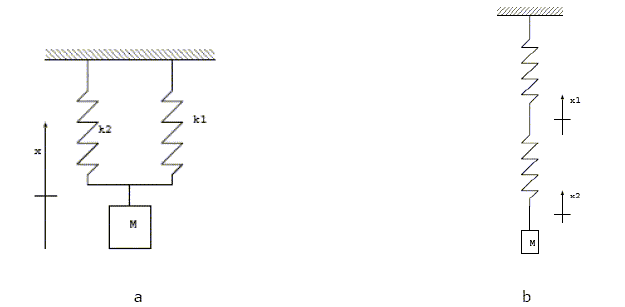
La période est proportionnelle à la racine carrée de la masse. La période d'oscillation de la masse M à vide est de 2p(M/k)½ où k est la constante de raideur du ressort. Vrai. On considère deux ressorts identiques de même raideurs k. On peut les combiner ensemble soit en série (a) soit en parallèle (b).
Le ressort équivalent dans le cas a a une raideur K=2 k. Vrai. A l'équilibre Mg = k1x+k2x=(k1+k2)x = Kx. Le ressort équivalent dans le cas b a une raideur K=½k. Vrai.
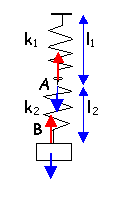
en B : Mg= k2(l2-l'0) L'allongement du système est DL= ( l1+ l2) -(l0 + l'0) DL =( l2- l'0) + ( l1- l0) =( l2+ l'0) +k2 /k1(l2-l'0) DL =( l2- l'0)[ 1+k2 /k1] Mg= k2 / [ 1+k2 /k1] DL raideur du ressort unique : k2 / [ 1+k2 /k1]=k1k2 / ( k1+ k2) longueur à vide de ce ressort : l0 + l'0 si les deux ressorts sont identiques : 0,5 k et 2lo |
||||||||||
|
|
||||||||||
|
|
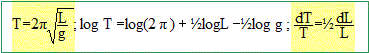
x"+k/m
x=0.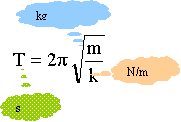
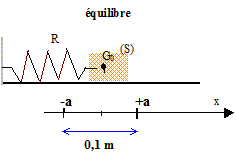k = 20 N/m.
