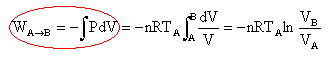Aurélie 01/02
cycles réalisés avec un gaz parfait

une seule source : récepteur

à l'aide de deux sources

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

Le cycle comprend une isotherme AB, une adiabatique CA, une isochoreBC. La masse de gaz est constante.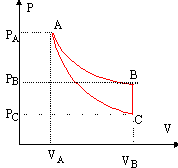

  1. On dispose d'une seule source de chaleur ; sa température est celle de l'isotherme. Peut-on réaliser un cycle moteur ? Justifier.
  2. On étudie le cycle ABCA. Les transformations sont réversibles. La masse d'air, assimilé à un gaz parfait est m = 1 g. Masse molaire 29 g/mol ; Cp / Cv = g = 1,4= constante.
    VA = 8 10-5 m3 ; PA = 10 bars = 106 pascals. PA / PC = 10.
    - Calculer TA, TB, TC, PB, TC, VB, VC.
    - Calculer les travaux échangés avec l'extérieur au cours des transformations AB, BC, CA.
    - Calculer les quantités de chaleur échangés avec l'extérieur au cours des transformations AB, BC, CA.
    - Calculer le travail et la quantité de chaleur échangés avec l'extérieur au cours du cycle.

 

corrigé
La variation d'entropie DS est nulle sur le cycle.

la variation d'entropie est égale à la somme de l'entropie échangée et de l'entropie crée : DS = S éch + S crée.

 or S crée est positive ou nulle ; donc S éch est négative ou nulle

or S éch = Q / T donc Q négatif ou nulle.

La variation d'énergie interne est nulle sur le cycle. DU = Q + W =0

Q étant négatif alors le travail W est positif.

conclusion : une seule source de chaleur étant disponible, alors le système:

- céde un transfert thermique vers l'extérieur Q <=0

- reçoit du travail W>=0

c'est un récepteur.

Quantité de matière : n =1 /29 = 3,45 10-2 mol.

Au point A : TA = PA VA / (nR)= 106 * 8 10-5 /(3,45 10-2 *8,32) =279 K.

la transformation AB étant une isotherme alors TB = 279 K.

Au point C : pour une transformation adiabatique réversible : PA VA g =PC VC g .

VC g = PA / PC VA g = 10 (8 10-5)1,4 soit VC = 10 1/1,4 *8 10-5 = 4,14 10-4 m3.

la transformation BC étant une isochore alors VB = 4,14 10-4 m3.

TC = PC VC / (nR)= 105 * 4,14 10-4 /(3,45 10-2 *8,32) =144,2 K.

Au point B : la transformation AB est une isotherme PA VA = PB VB.

PB =PA VA / VB = 106 * 8 10-5 / 4,14 10-4 = 1,93 105 Pa.

travail lors de la transformation isotherme AB :

WA-->B = -3,45 10-2 *8,32 *279 ln(41,4 / 8) = -132 J.

au cours de la transformation BC isochore, le volume reste constant : le travail est nul.

au cours de la transformation adiabatique CA, pas déchange de chaleur avec l'extérieur, le travail mis en oeuvre est égal à la variation d'énergie interne du gaz.

WC-->A = DU = nCv(TA-TC) = n R /(g -1)(TA-TC)

WC-->A =3,45 10-2 *8,32 / 0,4 *(279-144,2)= 98 J.

travail total sur le cycle : -34 J.

chaleur échangée lors de la transformation isotherme AB :

la température est constante, alors la variation d'énergie interne est nulle.

DU = WA-->B +QAB = 0

QAB = -WA-->B =132 J.

au cours de la transformation adiabatique CA pas de transfert thermique.

au cours de la transformation BC isochore, le volume reste constant : le travail est nul.

DU = QBC = nCv(TC-TB) = n R /(g -1)(TC-TB)

QBC = 3,45 10-2 *8,32 / 0,4 *(144,2-279)= -98 J.

soit Q total = +34 J.

Deux sources de chaleur sont nécessaires pour réaliser réversiblement un cycle composé de deux isothermes AB et CD et deux isochores BC et DA. La masse de gaz est identique à celle de la première partie.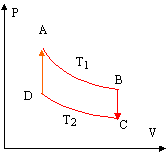

  1. En fonction des paramètres VA, T1, T2, PC, établir les expressions :
    - de la quantité de chaleur totale Q1 reçue par le système au cours d'un cycle moteur réversible.
    - de la quantité de chaleur totale Q2 cédée par le système au cours d'un cycle moteur réversible.
    - du rendement thermodynamique du cycle     h= -W/ Q1.
    - Exprimer le rendement thermodynamique du cycle de Carnot (les températures des sources sont égales aux températures extrêmes précédentes) ?
    - Comparer les deux rendements et conclure.
    - applications numériques : VA= 8 10-5 m3 ; PA = 4 106 pa; PC = 105 Pa ; T2 = 300 K.
corrigé
isotherme AB :

la température étant constante, la variation d'énergie interne est nulle

DU = Q + W =0 soit Q = -W  

travail élémentaire des forces de pression : dW = -PdV

PV = nRT1 donne PdV + VdP = 0 soit dW = VdP = nRT1 / P dP = nRT1 d ln P

travail W A-->B = nRT1 ln(PB /PA)

QA-->B = nRT1 ln(PA /PB) positif car PA >PB

de même sur l'isotherme CD : Q C-->D = nRT2 ln(PC /PD) négatif car PC <PD

isochore BC :

le travail des forces de pression est nul et la variation d'énergie interne du gaz est égale à QB-->C

DU = QB-->C = nCv(TC-TB) = n R /(g -1)(T2-T1) négative car T2<T1

de même sur l'isochore DA :

DU = QD-->A = nCv(TD-TA) = n R /(g -1)(T1-T2) positive car T2<T1

transfert Q1 positif :

Q1 = nRT1 ln(PA /PB) + n R /(g -1)(T1-T2).

transfert Q2 négatif :

Q2 =nRT2 ln(PC /PD) + n R /(g -1)(T2-T1)

rendement :

la variation d'énergie interne est nulle sur le cycle donc W +Q1 + Q2 = 0

h= -W/ Q1 = (Q1 + Q2 )/ Q1 = 1 + Q2/ Q1

h = 1+ [T2 ln(PC /PD) + 1 /(g -1)(T2-T1)] / [T1 ln(PA /PB) + 1 /(g -1)(T1-T2)]

or PD = nRT2/ VA et PA / PB = VB / VA =VC / VD = nRT2/ (PCVA)

h = 1+ [T2 ln(PCVA /(nRT2)) + 1 /(g -1)(T2-T1)] / [T1 ln(nRT2/ (PCVA)) + 1 /(g -1)(T1-T2)].

h = 1+a T2/T1

avec a = ln(PCVA /(nRT2)) + 1 /(g -1)(1-T1/T2)] / [ ln(nRT2/ (PCVA)) + 1 /(g -1)(1-T2/T1)].

le rendement du cycle de Carnot est : hcarnot = 1 - T2 / T1.

si a est inférieur ou égal à -1 alors h <= hcarnot .

a est-il bien inférieur à -1?

ln(PCVA /(nRT2)) + 1 /(g -1)(1-T1/T2)] <= -[ ln(nRT2/ (PCVA)) + 1 /(g -1)(1-T2/T1)].

1-T1/T2<= -1+T2/T1 soit 2 <=T2/T1 +T1/T2 soit (T1-T2 )>0 vrai.

applications numériques :

T1 = 8 10-5*4 106/(8,32*3,4510-2) = 1114,8 K.

PA /PB=0,0345*8,32*300 / 8 = 10,76

Q1 = 3,45 10-2 *8,32[1114,8 ln 10,76 + 1 /0,4 *(1114,8-300)] = 1345 J.

Q2 = 3,45 10-2 *8,32 [300 ln(1/10,76) + 1 /0,4(300-1114,8)]= -789 J.

h= 1- 789 / 1345 = 0,41.

hcarnot= 1 -300/1114,8 = 0,73.

retour - menu