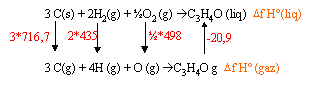Aurélie 01/02
enthalpie, déplacement d'un équilibre

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

 

L'acroléïne CH2=CH-CHO est un liquide dans les conditions standarts à 298°C.

  1. Déterminer l'enthalpie standart de formation de l'acroléïne à partir de son énergie de combustion.
  2. Même question à partir des énergies de liaisons . Comment expliquer la différence ?

données : DH° combustion acroléine = -1630 kJ/mol ; DH°(H2O liq) = -285,3 kJ/mol ; DH°(CO2 gaz) = -393,5 kJ/mol ;

DH° sublimation C(s) = 716,7 kJ/mol ; DH° vaporisation acroléine (liq) = 20,9 kJ/mol ;

enthalpie de formation des liaisons (kJ/mol )
H-H
O=O
C=C
C=O
C-C
C-H
H-H
435
498
620
720

804 dans CO2
340
415
436

corrigé
combustion acroléïne :  

C3H4O (liq) + 3,5 O2 donne 3 CO2 (gaz) + 2 H2O (liq)

DH° combustion = 2 DH° (H2O(liq)) + 3 DH°(CO2 (gaz)) - Df H°(C3H4O (liq))

Df H°(C3H4O (liq)) = 2 DH° (H2O(liq)) + 3 DH°(CO2 (gaz)) - DH° combustion

Df H°(C3H4O (liq)) = 2*(-285,3) + 3*(-393,5) - (1630) = -121,1 kJ/mol.

à partir des énergies de liaisons :  

réaliser un cycle

 

Df H°(C3H4O (liq)) = 3*716,7 +870 +249 + Df H°(C3H4O (gaz) -20,9 = 3248,2 +Df H°(C3H4O (gaz)

liaisons créees : C=C ; C=O; 4 C-H ; C-C

Df H°(C3H4O (gaz) = - S énergies de liaisons des liaisons créees + S énergies de liaisons des liaisons rompues

Df H°(C3H4O (gaz) = -620 +-340 -4*415 -720 = -3340 kJ/mol

Df H°(C3H4O (liq)) = 3248,2 -3340 = -91,8 kJ/mol.

le calcul à partir des énergies de liaisons est imprécis et donne seulement un ordre de grandeur.

Soit la réaction équilibrée CO(g) + H2O(l) = CO2(g) + H2(g) avec Df H° = -43,51 kJ/mol

  1. En appliquant les lois de déplacement de l'équilibre préciser l'influence :
    - de la pression
    - d'une augmentation de la température.
    - d'une augmentation de la concentration de la vapeur d'eau.
  2. Donner l'expression de la constante d'équilibre K en fonction des pressions partielles des constituants du mélange à l'équilibre.
  3. A 450°C la constante K vaut 7,14. On porte à 450°C sous pression constante 105 Pa un mélange constitué de 1 mole d'eau et une mole de CO. Quelle est la composition du mélange gazeux quand l'équilibre est atteint ?
    - Quelle serait la composition si le mélange initial était constitué d'une mole de CO et de 10 mol d'eau ?
  4. Calculer la valeur de K à 350°C en supposant les enthalpies indépendantes de la température.
corrigé
La preesion n'a aucune influence car le nombre total de moles reste constant

une augmentation de température favorise une réaction endothermique, donc déplacement de l'équilibre vers la gauche.

l'augmentation de la concentration de la vapeur d'eau déplace l'équilibre à droite, consommation de la vapeur d'eau
CO
H2O
CO2
H2
initial
a (mol)
b (mol)
0
0
date t
a-x
b-x
x
x
pression partielle
(a-x)P / (a+b)
(b-x)P / (a+b)
xP / (a+b)
xP / (a+b)
nombre total de mol : a+b ; P : pression totale.

constante d'équilibre : K = PH2 * PCO2 / (PH2O * PCO)

K = x² / [(a-x) (b-x)] indépendant de la pression totale.

si a=b=1 mole alors à 450°C :K =7,14

7,14(1-x)(1-x) = x²

6,14 x² -14,28 x + 7,14 =0

résoudre x = 0,728 mol.

composition du mélange : 0,728 mol H2 et CO2; 0,272 mol H2O et CO.

si a=1 et b=10 mol alors à 450°C :K =7,14

7,14(1-x)(10-x) = x²

6,14 x² -71,4 x + 64,26 =0

résoudre x = 0,993 mol.

composition du mélange : 0,993 mol H2 et CO2; 9,017 mol H2O et 0,017 mol CO.

l'équilibre précédent a bien été déplacé à droite.

influence de la température :

d lnK / dT = D H° / (RT²)

dlnK = D H° / R d(-1/T)

intégrer entre T1 = 450+273 = 723 K et T2 =350+273 = 623 K

ln (K2/ K1 ) =D H° / R(1 / T1 - 1/T2 ) avec K1 =7,14

ln (K2 / 7,14) = -43510 / 8,31 ( 1 / 723 -1 / 623) = 1,135

K2= 7,14 exp 1,135 = 22,25.

une diminution de température en passant de 450°C à 350°C favorise la réaction exothermique ; déplacement de l'équilibre à droite et augmentation de K. 

retour - menu