Jeu de billes et gravité. Bac
Métropole 09 /2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Le
mouvement de la bille est étudié dans le référentiel terrestre supposé
galiléen. À la date t = 0, la bille est lâchée sans vitesse initiale du
point A situé en haut d’une tour de hauteur H. Elle roule ensuite sans
glisserjusqu’au point B, en ligne droite le long d’un rail de longueur L.
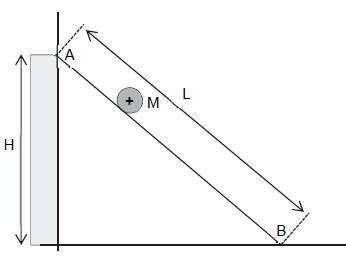
masse de la bille m = 8,51 g ; volume de la bille V = 1,07 cm3.
Q1. Déterminer la masse volumique r de la bille. En déduire la nature probable du matériau qui la constitue.
m / V = 8,51 / 1,07 =7,95 g / cm3. (acier).
On relève la position de la bille par chronophotographie. On détermine
alors, par un traitement numérique, la valeur de la vitesse v de la
bille à chaque instant, puis on représente graphiquement les
évolutions au cours du temps de son énergie cinétique Ec, de son
énergie potentielle Ep et de son énergie mécanique Em.
Q2. Identifier,
parmi les courbes 1, 2 et 3, en justifiant, la courbe représentant
l’évolution de l’énergie cinétique ainsi que celle représentant
l’évolution de l’énergie potentielle de pesanteur.
La vitesse croît au cours de la descente : l'énergie cinétique augmente.
L'altitude diminue lors de la descente et l'énergie potentielle diminue.
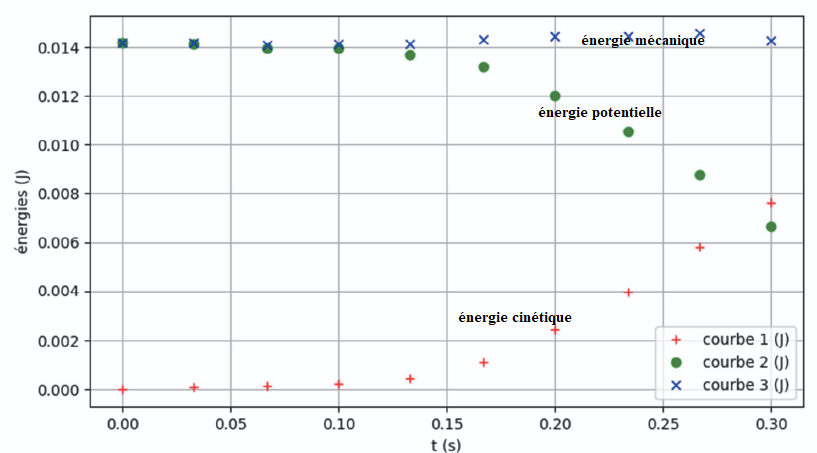
Q3. Décrire l’évolution temporelle de l’énergie mécanique de la bille à partir des données expérimentales.
Commenter.
L'énergie mécanique est à peu près constante : les frottements sont négligeables.
Les données précédentes ont été obtenues en étudiant le mouvement de la bille dans le repère d’espace
(Ox ; Oz). Les coordonnées du centre de masse sont notées x(t) et z(t).
L’origine de l’énergie potentielle de pesanteur de la bille est prise
lorsque son centre de masse est à la position z = 0.
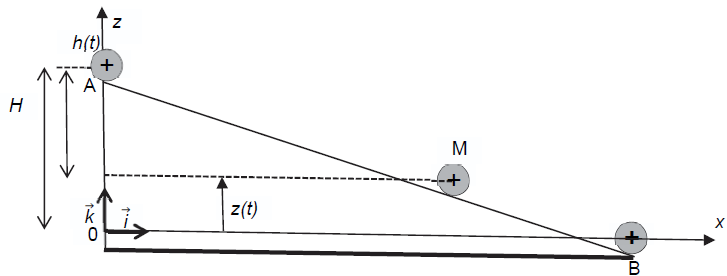
Un programme, écrit en langage Python, a permis d’obtenir les données précédentes. Deux extraits en sont donnés.
La variable N correspond ici au nombre d’images pointées sur la vidéo du mouvement de la bille allant du point A au point B.
La fonction range(a,b) renvoie les entiers de a à b-1 par pas de 1. Les valeurs des variables x, z et t sont
stockées dans des tableaux x, z et t, indicés de 0 à N-1.
Q4. Expliquer pourquoi le programme présenté ne permet pas de calculer l’énergie cinétique aux points A et B.
Pour le calcul de la vitesse en un point, le programme utilise le point d'avant ( i-1) et le point d'après ( i+1).
A étant le premier point, il n'y a pas de point d'avant. B étant le derrnier point, il n'y a pas de point d'après.
Q5. Recopier et
compléter les lignes 81 et 84 du programme écrit en langage Python
présenté afin qu’il calcule les énergies potentielle Ep et mécanique Em.

Lors du mouvement étudié sur cette portion du circuit, la bille roule
sans glisser. Son énergie cinétique, qui tient compte de la rotation de
la bille sur elle-même, est exprimée par la relation suivante :
Ec = 0,7 mv2.
Q6. En appliquant
la conservation de l’énergie mécanique entre l’instant initial t = 0 et
l’instant t, montrer que l’expression de la vitesse de la bille à
l’instant t s’écrit :
v(t) =( 10 / 7 g h(t))½.
avec h(t) la hauteur de chute, c’est-à-dire la différence d’altitude du
centre de masse de la bille entre l’instant initial t = 0 et l’instant
t.
Energie mécanique initiale : m g H.
Energie mécanique à la date t : m g z(t) + 0,7 m v(t)2.
Conservation de l'énergie mécanique : m g H = m g z(t) + 0,7 mv(t)2.
m g(H-z(t) = mgh(t) =0,7 mv(t)2.
gh(t) =0,7 v(t)2.
v(t) = (g h(t) / 0,7)½.
|
...
= =
|
....
|
L’évolution
observée du carré de la vitesse en fonction de la hauteur de chute h(t)
est représentée. Les points expérimentaux sont modélisés par une droite
d’équation :
v2(t) = k·h(t).
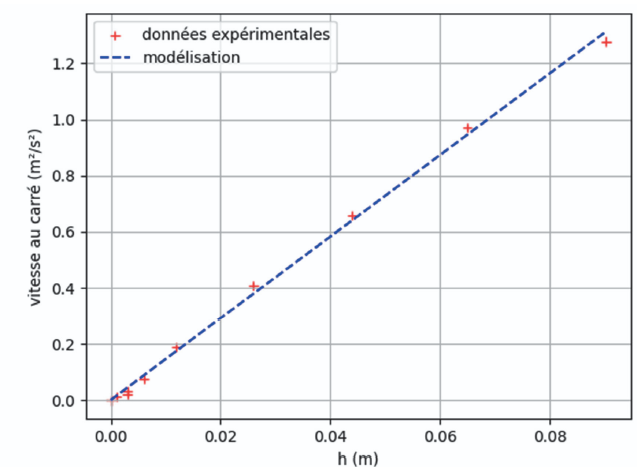
Q7. Justifier que l’équation de la modélisation est cohérente avec l’expression donnée en Q6.
v2(t) =g / 0,7 h(t) .
Droite passant par l'origine : fonction linéaire de coefficient directeur k=g / 0,7.
Q8.
Déterminer la relation entre l’intensité de la pesanteur g et la
constante k. Calculer la valeur de l’intensité de la pesanteur g dans
cette expérience, sachant que l’analyse des résultats donne la
valeur k = 14,53 m·s–2.
g = 0,7 k = 0,7 * 14,53 ~10,2 m s-2.
On reproduit sept
fois la chute de la bille et on rassemble les valeurs de l’intensité de
la pesanteur déterminées pour chacune des expériences dans le tableau
suivant :
expérience
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
valeur expérimentale de g (m s-2)
|
10,17
|
9,70
|
9,81
|
10,19
|
10,32
|
10,32
|
9,42
|
9,89
|
Un traitement statistique des données du tableau précédent permet
d’obtenir que l'incertitude-type sur la mesure de l’intensité moyenne
de la pesanteur est u(gmoy) = 0,11 m·s–2.
Q9. Discuter de
l’accord du résultat de la mesure de l’intensité moyenne de la
pesanteur issu des huit expériences avec sa valeur de référence.
Conclure sur l’utilisation de cette méthode pour mesurer la valeur de
l’intensité de la pesanteur avec ce jeu.
Valeur moyenne de g : 9,98 ±0,11 m s-2.
|(g-gréf) / u(g)| =|(9,98-9,81) / 0,11| =1,5 < 2.
Le résultat de la mesure est compatible avec la valeur de réérence.
Cette méthode est valable pour mesurer la valeur de
l’intensité de la pesanteur avec ce jeu.
|
|
|
|