Le réfrigérateur. Bac Métropole 09 /2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . ... . . ... .. .. ...... ... Les objectifs de cet exercice sont :  - d’étudier dans une première partie le refroidissement d’une bouteille d’eau placée dans un réfrigérateur « A » destiné à maintenir au frais des boissons à la température d’environ 7 °C  - d’étudier dans une seconde partie la difficulté d’ouverture d’une porte d’un réfrigérateur « B » dans deux situations différentes. 1. La température « idéale » d’une bouteille d’eau pour optimiser l’hydratation  Données :  le système étudié dans cette partie est une bouteille d’eau notée S ;  volume du système S : VS = 1,5 L ; masse volumique du système S : rS = 1,00 kg·L–1 ;  capacité thermique massique du système S : cS = 4,18×103 J·K–1·kg–1 ;  la température idéale de consommation de l’eau, afin d’optimiser la réhydratation du corps humain, est : qdéale = 16 °C ;  la loi de Newton donne l’expression du flux thermique F (en W) reçu par le système S, à une température q(t), de la part de l’air intérieur du réfrigérateur dont la température qréfri est considérée constante F = a·(qréfri – q(t)) où a = 0,50 W·K–1 est une estimation du coefficient d’échange thermique entre le système S et l’air intérieur du réfrigérateur. À l’instant t = 0, on place le système S dans le réfrigérateur « A », on ferme la porte de ce réfrigérateur puis on mesure la température q(t) du système S à intervalle de temps régulier pendant une demi-journée. Q1. Caractériser qualitativement le phénomène de convection, un des modes de transfert thermique ayant lieu entre S et son environnement. Transfert thermique dû au mouvement d'un fluide, liquide ou gaz. Q2. Indiquer, en justifiant, le sens du transfert thermique Q dans le cas étudié. Le transfert thermique s'effectue du corps chaud, la boutielle d'eau, vers le corps froid, l'intérieur du réfrigérateur. 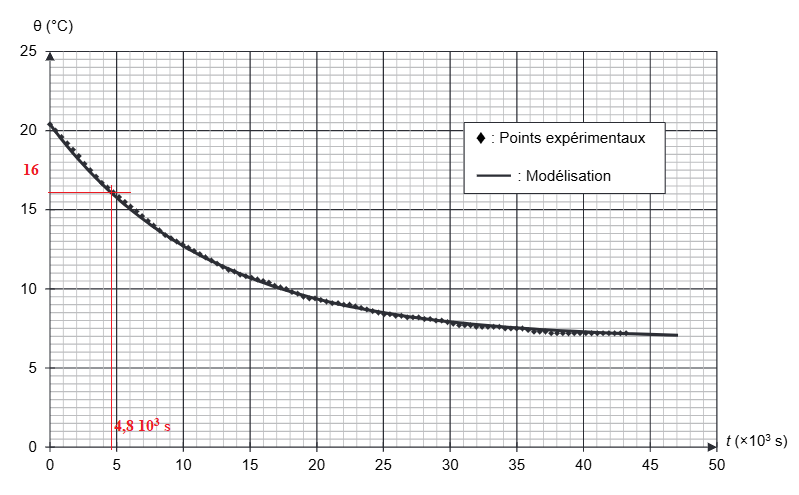L’utilisation d’un tableur-grapheur permet d’obtenir :  - le tracé de la courbe de température expérimentale à partir des mesures effectuées ; - le tracé d’une courbe de modélisation de l’évolution temporelle de la température q(t) du système S à l’aide d’une fonction de la forme générale : q(t) = A·exp(-t / t) + B où A, B et t sont des constantes.  Ces deux courbes sont représentées. Q3. Exprimer q(t = 0) puis la limite de q(t) quand t --> +∞ en fonction des constantes A et B. En déduire, en utilisant la figure des valeurs des constantes A et B en précisant leur unité respective. 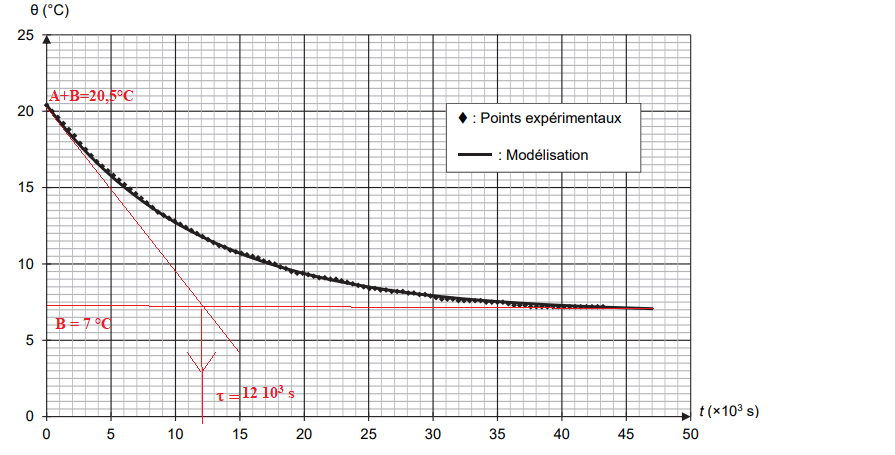Quand t tend vers +oo, q(t) = B =7°C. q(t = 0)=A +B=20,5°C ; A = 13,5°C..  Q4. Montrer graphiquement, en faisant apparaître la construction sur la figure, que la valeur de la constante t est de l’ordre de 12×103 s. On cherche à déterminer par un modèle l’équation différentielle vérifiée par la fonction q(t). Pour cela, on effectue un bilan d’énergie pour le système S, entre les instants t et t + Dt. Q5. Appliquer le premier principe de la thermodynamique au système S entre t et t + Dt pour exprimer la variation de température q(t + Dt) – q(t) en fonction de Dt, ρS, VS, cS, a et (qréfri – q(t)). DU =,W + Q avec W=0 dans ce cas. Q = mS cS Dq = ρS, VS cS (q(t + Dt) – q(t)) . F =Q / Dt ; F = a(qréfri – q(t))/ Dt = ρS VS cS (q(t + Dt) – q(t)) q(t + Dt) – q(t)=a(qréfri – q(t)) / ((ρS VS cS)Dt). On en déduit que l’équation différentielle régissant l’évolution de la température q(t) s’écrit : dq(t) dt + q(t) / t = θréfri / t avec t = ρS VS cS / a . La solution de cette équation différentielle a pour expression : q(t) = (q0 – qréfri)·exp(-t / t) + qréfri . On donne pour l’expérience réalisée : q0 = 20,4 °C et qréfri = 6,8 °C. Q6. Établir, selon cette modélisation, en fonction de t , q0, qréfri et qidéale, l’expression de la durée tidéale nécessaire pour que le système S atteigne la température idéale de consommation d’une boisson. qidéale = (q0 – qréfri)·exp(-tidéale / t) + qréfri qidéale -qréfri =(q0 – qréfri)·exp(-tidéale / t) (qidéale -qréfri) / (q0 – qréfri)= exp(-tidéale / t) ln((q0 – qréfri) /(qidéale -qréfri) )= tidéale / t ; tidéale = t ln((q0 – qréfri) /(qidéale -qréfri) ) Q7. Calculer cette durée tidéale. Indiquer si cette durée est cohérente avec le graphique ci-dessous. Une construction graphique est attendue. t = ρS VS cS / a =1 x 1,5 x4,18 103/ 0,50=1,254 104.s ln((q0 – qréfri) /(qidéale -qréfri) )=ln((20,4-6,8) / (16-6,8))=0,39. tidéale =1,254 104.x 0,39 =4,9 103 s. Résultat en accord avec le graphe ci-dessous. ... =  = .... 2. Ouverture de la porte du réfrigérateur « B » Dans des conditions d’usage régulier, l’ouverture de la porte d’un autre réfrigérateur nommé « B » est parfois difficile. Un élément d’explication de cette difficulté peut être envisagé en considérant la différence de pression entre l’air intérieur du réfrigérateur et l’air extérieur à celui-ci. Mise en service du réfrigérateur.  On étudie l’influence du changement de température lors de la mise en service du réfrigérateur sur la différence de pression. Données :  l’air est considéré comme un gaz parfait ;  constante des gaz parfaits : R = 8,314 J·K–1·mol–1 ;  équation d’état du gaz parfait : P·V = n·R·T avec P la pression du gaz en Pa, V le volume occupé par le gaz en m3, n la quantité de matière de gaz en mol et T la température du gaz en K ;  volume d’air dans le réfrigérateur : Vréfri = 0,15 m3 ;  température de l’air ambiant extérieur au réfrigérateur : Tamb = 293 K ;  pression de l’air ambiant extérieur au réfrigérateur : Pamb = 1009,1×102 Pa ;  intensité de la pesanteur : g = 9,8 N·kg–1. À la date t = 0, la porte du réfrigérateur, contenant de l’air à la température T0 = Tamb et à la pression P0 = Pamb, est fermée puis le réfrigérateur est mis en fonctionnement. On note T et P, respectivement la température et la pression de l’air intérieur du réfrigérateur à une date quelconque. On fait l’hypothèse que le réfrigérateur constitue un système fermé, lorsque la porte est fermée : il n’échange pas de matière avec l’extérieur.  Q8. Expliquer pourquoi, dans le cadre de cette hypothèse, le quotient P /T peut être considéré constant lors du refroidissement de l’air du réfrigérateur après la fermeture de la porte. Porte fermée : le volume du gaz situé à l'intérieur et la quantité de matière de ce gaz sont constants. P / T = nR / V = constante. Q9. Calculer, dans ce modèle, la valeur, notée Pfinale, de la pression de l’air à l’intérieur du réfrigérateur lorsque la température intérieure a atteint sa valeur stabilisée égale à 277 K. Pfinale / 277 = Pamb / Tamb = 1009,1 102 / 293 =344,4. Pfinale =344,4 x277 =9,54 104 = 954 102 Pa. En réalité, on mesure à cette température une pression intérieure finale voisine de 1009,1×102 Pa. Q10. Indiquer une raison possible de l’écart entre le résultat du calcul effectué à la question Q8 et la pression réellement mesurée. L'hypothèse que la réfrigérateur est un système fermé est fausse. Difficulté d’ouverture d’une porte de réfrigérateur juste après sa fermeture.  Dans certains cas, la réouverture d’une porte de réfrigérateur juste après fermeture, peut s’avérer difficile. Afin d’expliquer ce phénomène, on enregistre la pression de l’air à l’intérieur du réfrigérateur lors d’une expérience pour laquelle, le réfrigérateur étant ouvert, on en ferme la porte à un instant t1. L’évolution de la pression mesurée est représentée sur la figure . On s’intéresse à la réouverture la porte après une durée Dt suivant la fermeture. Q11. À l’aide de la figure , justifier qu’il peut être difficile de rouvrir la porte du réfrigérateur après une durée Dt = 3 s. La pression intérieure est inférieure à la pression extérieure. La résultante globale des force pressantes est dirigée de l'extérieur vers l'intérieur. Q12. En assimilant la porte du réfrigérateur à une plaque rectangulaire solide très fine de surface Splaque = 1,2 m2, déterminer la valeur et la direction de la résultante Fdes forces pressantes qui s’appliquent  sur cette plaque lorsque l’on souhaite rouvrir la porte après une durée Δt = 3 s. Commenter le résultat obtenu. F = DP S =(1009,1-1008,55) 102 x 1,2 =66 N. Cette force est faible ; on la compense en tirant sur la porte.

menu