Aurelie 03/ 02
une bobine inductive et deux condensateurs

Concours kiné 01 Ceerrf

suite --> pendule

Google

 

On réalise le montage ci dessous. Les deux condensateurs sont identiques C1=C2=C =2 10-7 F et la résistance de la bobine est négligée. L=0,1 H et E=10 V.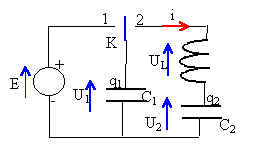

 

  1. Les deux condensateurs sont déchargés et on ferme K en position 1. Calculer la charge Q acquise par le condensateur1. Calculer l'énergie W emmagasinée.
  2. A la date t=0, on bascule K en position 2 :
    - Nommer le phénomène qui s'établit dans le circuit. Quelle relation peut-on écrire à tout instant entre les charges q1 et q2 des condensateurs et Q ? Justifier.
    - Donner en les justifiant les expressions des 3 tensions u1, u2 et uL en fonction de q1, q2 C et di/dt.
  3. En utilisant les relations précédentes, établir l'équation différentielle vérifiée par la charge q1 sous la forme q1 "+ A q1' =B
  4. Cette équation a pour solution q1=Q/2 (1+ cos(w0t)) avec w0² =A
    - Exprimer T0 période propre de l'oscillateur en fonction des données .
    - Calculer T0.
  5. Déterminer en fonction de W, la répartition de l'énergie dans le circuit à la date T0/4.
 

corrigé
charge maxi acquise par le condensateur n°1 : Q = C E = 2 10-7 *10 = 2 10-6 = 2mC.

énergie stockée : ½Q² /C = 0,5 * 4 10-12 / 2 10-7 = 10-5 J.

en fermant l'interrupteur en position 2, le circuit est le siège d'oscillations électriques libres; échange permanent d'énergie entre condensateurs et bobine.

la charge électrique reste constante (se conserve) : Q =q1 + q2.

u1 = q1/C ; u2 = q2/C ; uL =L di/ dt = -Ld²q1 /dt²

avec i = dq2 /dt = - dq1 /dt ( décharge du condensateur n°1 et charge du condensateur n°2)

aux bornes d'appareils en série les tensions s'ajoutent :

u1 = u2 + uL

q1/C = (Q-q1) / C -Ld²q1 /dt²

Ld²q1 /dt² + 2q1/C = Q/C

d²q1 /dt² + 2q1/(LC) = Q/(LC).

période :

w0² = 2/(LC) et T0 = 2p/w0

w0² =2 / (0,1 * 2 10-7 ) = 108 et w0 = 104 rad/s.

T0 = 6,28 10-4 s.

répartition de l'énergie à t= T0/4 : w0T0/4 = 2p/T0 * T0/4 = p /2.

q1 = ½ Q ( 1+ cos p /2 ) = ½ Q donc q2 = ½ Q

énergie totale stockée : ½ Q²/C

énergie stockée par le condensateur n°1 : ½ q1² / C = 0,125 Q² / C ( soit 25% de l'énergie totale)

énergie stockée par le condensateur n°2 : ½ q2² / C = 0,125 Q² / C ( soit 25% de l'énergie totale)

énergie stockée par la bobine : ½ Q² / C -0,125 Q² / C-0,125 Q² / C = 0,25 Q² / C ( soit 50% de l'énergie totale)
retour - menu