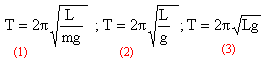Aurélie dec 2001
pendule simple

sage femme Ile de France 2001

exercice suivant : circuit RC

Google

Les horloges anciennes donnent l'heure grâce à un balancier qui oscille réguliérement et qui bat la seconde, c'est à dire qu'il effectue un aller retour - menu en 2s. Le balancier est assimilé à un pendule simple constitué d'un fil de masse négligeable, de longueur L à l'extrémité duquel est fixée une masse m égale à 200 g.

On donne g =9,81 m/s² nà Paris ; si q <20° alors sin q = q (rad) et cosq = 1-½q² (rad).

  1. Par analyse dimensionnelle, choisir l'expression correcte de la période en justifiant pour chaque expression proposée sa dimension :
  2. Calculer la longueur du pendule qui bat la seconde.
  3. En 1671, l'astronome français Richer s'aperçoit qu'en Guyane, le même pendule bat moins vite qu'à Paris. Calculer l'écart en ms entre les deux périodes sachant que l'intensité du champ de pesanteur vaut 9,78 m/s² en Guyane.
    - Quel facteur peut-on modifier pour rétablir la même période qu' à Paris ?
    - En 1790 lors de l'établissement du système métrique, il a été proposé d'utiliser un pendule simple pour définir le mètre. Compte tenu des questions précédentes, indiquer pourquoi cette idée a été abandonnée.
  4. On écarte le pendule simple de sa position d'équilibre d'un angle q m = 8° par rapport à la verticale et on l'abandonne sans vitesse, à un instant pris comme origine des temps. On suppose d'abord les frottements négligeables par rapport aux autres forces mises en jeu.
    - Montrer que l'énergie mécanique E du système {terre pendule} est donnée par la relation :
    E= mgL(1-cosq) +½ mLq'² où q ' est la dérivée de q par rapport au temps.

    - Calculer l'énergie initiale à t=0. Comment évolue cette énergie au cours du temps ?
    - Quelle sera l'allure de la courbe q ² = f ( q '²). On utilisera l'approximation des petits angles.

  5. De l'équation précédente, on peut déduire l'équation différentielle du mouvement :
    Lq" + gq=0 où q " est la dérivée de q ' par rapport au temps..
    - Vérifier que q =qmcos(wt) est solution de cette équation ; en déduire l'expression de la pulsation w et retrouver celle de la période déterminée à la question 1 par l'analyse dimensionnelle.

corrigé

l'unité de l'expression se trouvant sous le radical doit être [s]² pour être homogène à une durée en seconde.

L est en mètre [m] ;

la masse m est en kg ; son inverse en [kg]-1.

g est en m s-2 et son inverse est en [m]-1[s]².

L / mg : [m][kg]-1[m]-1[s]² soit : [kg]-1[s]²

(1) est fausse.

L est en mètre [m] ; g est en m s-2 et son inverse est en [m]-1[s]².

L/g : [m] [m]-1[s]²soit [s]²

(2) est correcte.

L g : [m] [m][s]-2.

(3) est fausse.

élever l'expression (2) au carré : T² = 4 p² L /g d'où L = T² g / (4 p² )

L = 4*9,81 / (4*3,14²) = 0,995 m.

nouvelle période : L= 0,995 m et g =9,78 m/s²

T1 = 2*3,14 * racine carrée (0,995 / 9,78 ) = 2,0031 s

l'écart est de + 3,1 ms.

cet écart peut être annuler en diminuant légèrement la longueur du pendule.

Un tel dispositif ne peut pas être utilisé pour définir l'unité de longueur, car la période et en conséquence la longueur dépendent du lieu où l'on se trouve.

énergie mécanique :

somme de l'énergie potentielle de pesanteur et de l'énergie cinétique.

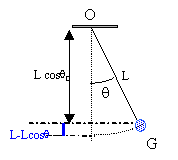
origine de l'énergie potentielle de pesanteur : la position d'équilibre

Ep = mgh = mg (L - L cosq)

énergie cinétique : ½mv² avec v = q ' L

Ec =½ m L² q '²

énergie mécanique : mg L( 1 - cosq) + ½ m L² q '² .

à t = 0 alors l'angle q est égal à zéro et la vitesse initiale est nulle

E = 0,2*9,81 * 0,995 (1 -cos8) = 0,019 J.

en absence de frottement cette énergie reste constante.

courbe q ² = f(q'²) :

mg L( 1 - cosq) + ½ m L² q '² = A = constante

diviser par mgL : ( 1 - cosq) + ½ L/g q '² = A / (mgL)

remplacer cos q par 1 -½q² : ½q² +½ L/g q '² = A / (mgL)

soit q² + L/g q '² = 2A / (mgL) = Cte.

q² = Cte - L/g q '² . droite

solution de l'équation différentielle : Lq" + gq = 0 ou q" + g / L q = 0

q =qmcos(wt)

la dérivée est : q '=qm(-w)sin(wt) ;

dériver à nouveau : q "= qm(-w) w cos(wt) = -w² qm cos(wt) = -w² q

repport dans l'équation différentielle :-w² q + g / L q = 0

l'égalité est vérifiée pour w² = g / L.

or T = 2p / w =2p racine carrée (L/g).

 

retour - menu