Aurélie dec 2001
circuit RC

sage femme Ile de France 2001

exercice suivant : circuit RLC

Google

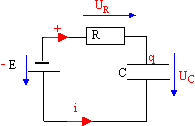
Etudions le circuit comprenant un générateur idéal E, un conducteur ohmique de résistance R et un condensateur de capacité C. R = 100 kW ; C= 1 mF et E=6V.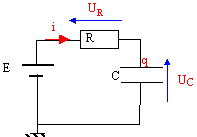

  1. Avec les conventions indiquées sur le schéma, donner les expressions de UR, UC, i.
  2. A l'instant t=0, le condensateur est déchargé :
    - établir l'équation différentielle vérifiée par UC(t).
    - vérifier que UC = E(1 - exp (-t / (RC)) est solution de cette équation.
    - On a relevé les valeurs de UC au cours du temps :
    t(s)
    0,1
    0,2
    0,3
    0,4
    0,5
    UC (V)
    3,82
    5,25
    5,71
    5,88
    5,96
    ln(1-UC/E)

    - Compléter le tableau puis tracer ln(1-UC/E) en fonction du temps.
    - Grâce au coefficient directeur de la droite obtenue, en déduire la valeur du produit RC.
    - On nomme t = RC constante de temps du circuit. Que représente physiquement cette grandeur ? Montrer qu'elle est homogène à un temps et la calculer à partir des caractéristiques du circuit. La comparer à la valeur trouvée graphiquement.
    - En déduire les expressions de q(t) et i(t), puis calculer q(t=5t ) et i (t= 1s). Commenter les valeurs obtenues.
  3. En réalité, le condensateur ne peut pas se charger entièrement car un dispositif approprié inverse les bornes du générateur quand UC=3 V. On prendra comme nouvelle origine des temps cet instant de basculement mais on conservera les conventions initiales de signe.
    - redessiner le circuit.
    - établir la nouvelle équation différentielle vérifiée par UC(t).
    - vérifier que UC = -E(1 - 1,5exp (-t / (RC)) est solution de cette équation.
    - calculer UC à t=0 et à t infini.
    - un nouveau basculement intervient quand UC=-3V. Calculer l'intervalle de temps Dt entre ces deux basculements.
corrigé
UR = Ri ; UC = q / C et i = dq /dt.

UR + UC = E soit Ri + UC = E ou encore R dq / dt + UC = E

avec i = d(CUC) / dt = C d(UC) / dt

donc : RC dUC / dt + UC = E

dériver UC = E(1 - exp (-t / (RC)) : U 'C = E / RC exp (-t / (RC))

repport dans l'équation différentielle : E exp (-t / (RC)) + E - E exp (-t / (RC)) = E égalité vraie.

t(s)
0,1
0,2
0,3
0,4
0,5
UC (V)
3,82
5,25
5,71
5,88
5,96
ln(1-UC/E)
-1
-2,08
-3,03
-3,91
-5,01

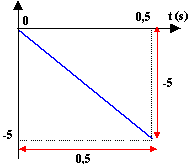
le coefficient directeur de cette droite est : -5/0,5 = -10.

UC = E(1 - exp (-t / (RC)) s'écrit :UC / E =1 - exp (-t / (RC)

soit 1 -UC / E =e xp (-t / (RC) ou ln(1 -UC / E) = -1/ (RC) t

le coefficient directeur de la droite est égal à -1 / (RC) d'où RC = 0,1 s.

R est équivalent à une tension (V) divisée par une intensité (A) : R : [V] [A]-1.

C la capacité est en coulomb divisé par une tension en volt : C : [C] [V]-1.

une charge en coulomb est équivalente à une intensité (A) fois un temps (s) doù la capacité : [A] [s] [V]-1.

unité du produit RC : [V] [A]-1 [A] [s] [V]-1= [s] .

R = 105 W ; C = 10-6 F et RC = 0,1 s.

charge et intensité :

charge q = CUC = CE(1 - exp (-t / (RC))

q(t=0,5) = 6 10-6( 1- exp(-0,5 /0,1)) = 0,993*6 10-6 = 5,96 10-6 C.

intensité i = dq/dt = -CE / (RC) exp (-t / (RC)

i ( t=1) = 6 10-6 / 0,1 exp(-1 / 0,1 ) = 2,7 10-9 A.

au dela de t = 5 fois la constante de temps on peut considérer que la charge du condensateur est complète ; l'intensité du courant est alors nulle.

décharge du condensateur puis charge en sens contraire :

 

on garde le même sens positif de parcours du circuit alors :

UR = -Ri ; i = -dq/dt : UC = -q /C

UR + UC = E soit - Ri + UC = -E

avec i = -d(CUC) / dt = -C d(UC) / dt

donc : RC dUC / dt + UC = -E

dériver UC = -E(1 - 1,5exp (-t / (RC)) : U 'C = -1,5 E / RC exp (-t / (RC))

repport dans l'équation différentielle : -1,5 E exp (-t / (RC)) - E +1,5 E exp (-t / (RC)) = -E égalité vraie.

UC(t=0 ) = -6 ( 1 -1,5) = 3V ;

UC(t infini ) = -6 ( 1-0 ) = -6V

cherchons la valeur de t correspondant à UC= -3V.

-3 = -6 (1 -1,5 exp (-t / 0,1))

3 / 6 = 1 -1,5 exp (-t / 0,1))

1,5 exp (-t / 0,1)) = 1-3 / 6 = 0,5

exp (-t / 0,1)) = 0,5 /1,5 = 1/3

-t / 0,1 = ln(1/3) = -1,0986

t = 0,1098 s. 

retour - menu