Aurélie sept 2000


devoirs en première S

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

Google


.
.

1

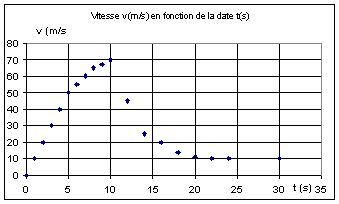
saut en parachute

(d'après lycée Bretagne)
Un parachutiste saute. Avec son équipement sa masse est 100 kg ( prendre g = 10 m.s-2 ). Le graphe donnant sa vitesse au cours de la chute est fourni.

  1. Vérifier que la chute est libre pendant les 5 premières secondes. (Phase A)
  2. Le parachute s'ouvre à t = 10s . Que se passe t il entre les dates 5 et 10 s ? (Phase B) puis entre 10 et 22 s (Phase C) et enfin après 22s (D) ? On précisera sur chaque phase le bilan des forces appliquées au parachutiste et leur effet sur le mouvement.
  3. En déduire sur la phase D l'intensité de la force de l'air sur le système.
  4. Cette force dépend de la surface S du parachute et de la vitesse v et d'une constante k s'exprimant en kg. m-3.Proposer une formule pour l'intensité de la force de frottement f en fonction de k, S et v.
  5. Calculer l'aire sous la courbe entre t = 0 et t = 5s. Calculer son unité en tenant compte des unités des axes (Indication l'aire ici n'est pas en m², l'unité dépend de l'unité de chaque axe de mesure). Réfléchir à ce que représente cette valeur.
  6. Il saute d'une altitude 645 m ! Sachant que l'aire mesurée entre t =5 et t = 22s vaut 510 u.S.I évaluer l'instant de l'impact au sol.
  7. Quelle est la vitesse moyenne pendant le saut .
corrigé
Pendant les 5 premières secondes de chute, parachute fermé, la courbe est pratiquement linéaire et le coefficient directeur de la droite est voisin de 10. En accord avec la relation théorique vitesse = g t = 10 t.

phase B:

Le parachutiste est soumis à son poids et à la résistance de l'air d'autant plus grande que la vitesse de chute est élevée. La résistance de l'air freine un peu le parachutiste. La chute n'est plus une chute libre et la vitesse est inférieure à 10 t.

phase C:

Le parachute est ouvert. Les forces de frottement sur les couches d'air deviennent très importantes. Le mouvement de chute est freiné : la vitesse de chute diminue.

phase D:

le poids et les forces de frottements se neutralisent (poids = frottement =1000N). Le mouvement de chute devient uniforme : la vitesse atteint une valeur limite et reste constante au voisinage de 10 m par seconde.

Il suffit de regarder les unités de chaque grandeur

aire comprise entre la courbe et l'axe des abscisses :

t appartient à :[0; 5s]

aire = vitesse * temps =ms-1*s = mètre

5*50/2 = 125 mètres

ou bien 10 t * t /2 = 5 t² = distance de chute libre.

phases b et c : l'aire indique la distance parcourue en mètre soit 510 m

phase a : 125 m parcourus soit en tout 635 m

phase d : mouvement uniforme 10 m parcouru par seconde

durée de la chute 23 s.

vitesse moyenne (m/s) = distance (m) / durée (s)

645 /23 = 28 m/s.


 


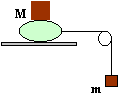
2

coefficient de frottement

Etudier expérimentalement le coefficient de frottement d'un savon sec ou humide.

  1. Matériel Un savon sec de masse ms =50g , eau , une poulie idéale + fil , masses marquées, une table lisse.

    Protocole On place sur le savon une Masse M, on suspend des masses marquées m dont le poids est transmis intégralement au savon par l'intermédiaire d'une poulie. On augmente m (gramme par gramme) jusqu'à ce que le savon commence à se déplacer , on note m la dernière valeur qui précède le déplacement.
    M (kg)
    50
    100
    500
    1000
    Savon sec m(g)
    60
    90
    330
    630
    savon mouillé m(g)
    30
    45
    160
    310
    Analyse

Etudier l'équilibre limite du système [savon + Masse] en général.

On appelle T la force de traction exercée par le fil (pour une poulie idéale T = m.g) ,

  • le poids total du système [ms+M] ,
  • N la réaction normale de la table,
  • f la force de frottement de la table sur le savon.
  1. Soit R la réaction de la table. Pour M = 500 g sur le savon sec. Faire un schéma des forces à l'échelle 1N -->1 cm.
  2. On appelle a0 l'angle limite que font R et N. Evaluer a0 . Montrer que tan( a0 ) dépend du rapport T / N et donc de m / (ms + M).
  3. Par analogie de raisonnement :

    Faire un schéma pour la même masse M mais savon mouillé. Evaluer a1

    Faire un schéma pour la masse 1000g et savon sec. Echelle 1N -->2 cm

    Evaluer a2

  4. Conclure sur la valeur de l'angle limite a et sa dépendance vis à vis de M et/ou la qualité du contact table - savon.
corrigé


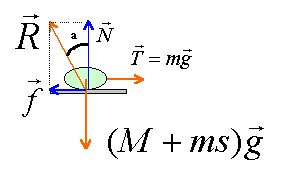
A l'équilibre la somme des vecteurs forces est nulle.

N= (M+ms)g et f = T = mg

tan (a) = mg / [(M+ms)g] = m/ (M+ms)

application numérique :
M = 500 g
M=1000 g
savon sec (angle a)
31°
31°
savon mouillé angle a)
16°
16°

La valeur de l'angle limite a dépend essentiellement de la qualité du contact ( savon mouillé ou non, rugosité du support ) et non de la valeur de la surcharge M.


devoir précédent
retour - menu
à suivre