|
|
d'après
concours kiné Limoges 2000
les
2 exercices suivants
|
|
1
charge du
condensateur
|
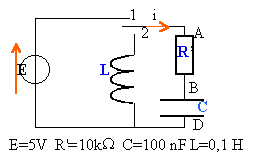
On place l'interrupteur en position 1 pendant quelques
secondes.
- Déterminer l'équation liant la tension
uBD, sa dérivée par rapport au
temps et les caractéristiques des composants du
circuit.
- Vérifier que uBD= E+A
e-bt
est solution de l'équation
précédente quelle que soit la valeur de A,
mais avec une valeur particulière de b
que l'on exprimera en fonction de certaines grandeurs du
circuit. Que représente 1/b.
Calculer sa valeur.
- Donner l'allure de la courbe uBD=f(t). On
déterminera comment sur la courbe
déterminer 1/b.
- Calculer l'énergie acquise par le condensateur
en fin de charge
corrigé
|
|
|
condensateur en série avec un résistor
et un générateur de tension continue : charge
du condensateur.
E = Ri + uBD.
avec q=CuBD et i= q'
=Cu'BD.(dérivée de la charge qpar
rapport au temps)
E = RC u'BD +
uBD.(1)
uBD= E+A e-bt
dériver : u'BD =-Abe-bt
remplacer dans
(1)
E= RC(-Abe-bt
) + E+A e-bt
vérifier quelque soit A à condition que
1/b =RC constante de temps du
dipole RC.
RC=104 *100 10-9=
10-3 s
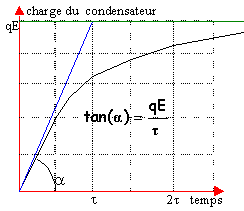
énergie acquise par le condensateur en fin de
charge :
0,5 CE² = 0,5 100 10-9 *5² = 1,25
microjoule.
|
|
2
décharge
du condensateur à travers la bobine
|
On bascule ensuite l'interrupteur en position 2
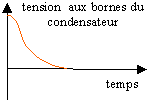
- Quelle est l'allure générale de la
courbe d'équation uBD=g(t) dans les 2
cas suivants : R' est faible; R' est très
élevée.
- On suppose R' nulle. Etablir l'équation
différentielle permettant de déterminer
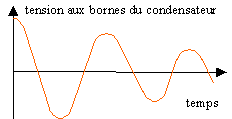
uBD(t). Donner l'allure générale
de la courbe d'équation uBD=h(t) et
calculer sa période.
corrigé
|
|
|
|
|
|
R' grande , régime
apériodique
|
R' peu élevée, régime
pseudopériodique
|
condensateur en série avec une bobine inductive de
résistance négligeable
tension aux bornes du condensateur plus tension aux
bornes de la bobine =0
u BD + L di/dt = u BD + L i'
avec i = q' = C u'BD donc i' = q" = C
u"BD .
u BD + L C
u"BD= 0
la courbe uBD = h(t) est une sinusoïde de
pulsation w = racine
carrée (1 / (LC))
de période T = 2 p
racine carrée (LC) = 6,28 racine carrée (
0,1*10-7)
T= 6,28 10-4 s.
|
|
3
dipole
RLC en régime forcé
|
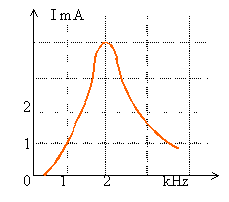
On étudie la réponse d'un circuit RLC
série pour un régime forcé
sinusoïdal imposé par un
générateur de tension. On relève
l'intensité efficace I du courant pour
différentes fréquences. Le
générateur maintient une tension de valeur
efficace U=0,8 V constante.
- Déterminer la fréquence de
résonance f0 : relever
l'intensité I0 de
résonance.
- Quelle est la bande passante b
à 3dB ? Quel est le facteur de qualité
?
- Le facteur de qualité est aussi égal
à Lw0 / R.
Déterminer les valeurs de la résistance
totale R, de l'inductance L et de la capacité C de
l'oscillateur.
- La résistance R du circuit est divisée
par 2 :
- Que devient la fréquence de résonance
?
- Calculer la nouvelle valeur de la bande passante
?
- Le circuit est-il: plus sélectif, aussi
sélectif, moins sélectif ?
corrigé
|
|
|
lecture graphique : f0 =2000 Hz et
I0=0,004 A
bande passante : ensemble des fréquences pour
lesquelles l'intensité est supérieure à
0,004 / 1,414 soit intensité supérieure
à : 0,0028 A
tracer une horizontale passant par 0,0028 A puis à
partir des intersections avec la courbe, tracer 2
verticales.La bande passante est l'ensemble des
fréquences comprises entre ces 2 verticales.
1,7 à 2,5 kHz soit b
voisin de 800 Hz
facteur de qualité : f0 / b
voisin de 2000/ 800 =
2,5.
à la
résonance d'intensité
:
- l'impédance du circuit est
minimale, égale à la résistance du
circuit
Ueff = R Ieff avec Ieff
= 0,004 A
R = 0,8 / 0,004 =
200
ohms.
- la fréquence du
générateur est égale à la
fréquence propre du dipole LC
2000= 1 / (2p racine
carrée (LC))
LC = 1 / (4p²*
2000²) = 6,34 10-9.
(1)
- la bande passante est égale à
Lw0 / R avec
w0 = 2
p f0 = 6,28 *2000 = 1,256
104 rad s-1.
d'où L= 2,5 * 200 / 1,256 104 =
40
mH.
repport dans
(1) : C = 6,34
10-9/ 0,040 =
1,58 10-7
F
la résistance du
circuit est divisée par 2 :
- le facteur de qualité double et
devient égal à 5.
- la fréquence propre du dipole Lc ne
change pas donc b= 2000/5 =400
Hz
- le circuit est plus sélectif, la bande
passante est plus étroite et le facteur de
qualité augmente.
retour - menu
|




