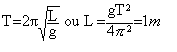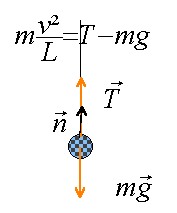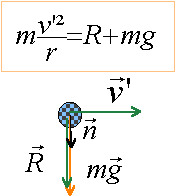|
|
|
|
entretien d'un pendule simple |
Intensité de la pesanteur g=10 m s-2 et p²=10 Le fil du pendule est toujours rectiligne dans sa totalité et tendu.
corrigé |
|
entre deux passages consécutifs et dans le même sens par la verticale il y a une période. donc T=2s.
conservation de l'énergie mécanique aux cours des premières oscillations : au départ, énergie cinétique : 0,5 mv² au point le plus haut, énergie potentielle de pesanteur : mgL(1 -cos qm) d'où : 1 -cos qm = 0,5 v² / (gL) cos qm = 1-0,5 v² / (gL) cos qm = 1-0,5*3,14² / (10*1)=0,5 qm = 60°. ensuite qm diminue du fait de l'amortissement. tension du fil au passage par la verticale : écrire la relation fondamentale de la dynamique du point dans la base de Frenet :
T=mg+mv²/L = 0,5*10+0,5*3,14² / 1 =10 N entretien des oscillations : l'énergie fournie au pendule compense à chaque période l'énergie perdue lors des frottements. énergie fournie au pendule à chaque passage par la verticale : mg DL= 0,5*10*0,2 = 1J soit 2 J par période.
|
|
|
retour - menu au point de départ |
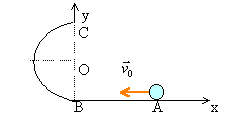 Une balle de mini golf assimilable à un point matériel est lancée à la vitesse V0 d'un point A vers un point B. AB est horizontal. En B la balle aborde l'intérieur d'un demi cylindre de rayon r, et ressort en C à la verticale de B. On néglige les frottements et on prend g=10 ms-2.
corrigé |
|
détermination de la vitesse minimale de passage en C ( l'action du support tend vers zéro pour cette vitesse minimale) l'expression ci dessus donne en faisant R=0 : v'² =g r = 10*0,9 = 9 donc v' = 3 ms-1. instant initial t=0 lorsque la balle passe en C. vecteur vitesse initiale (v' ; 0) vecteur position initiale ( 0 ; 2r) vecteur accélération (0 ;-g) vecteur vitesse, primitive du vecteur accélération (v' ; -gt ) vecteur position, primitive du vecteur vitesse ( x=v't ; y= -0,5 gt²+2r) éliminer le temps : t = x / v' et repport dans y y = -0,5 gx² / v'² +2r ( trajectoire ) or v'² =gr d'où y = -0,5 x² /r + 2r au point d'impact en A, y=0 0 = -0,5 x²A/ r +2r soit xA =2r. |