Métis un satellite en sursis. Bac G Nouvelle Calédonie 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.
.		 . .


.. ..
......


...
Plus imposante planète du système solaire, Jupiter est entourée de 95 satellites connus, ainsi que d’anneaux, beaucoup plus fins et sombres que ceux de Saturne. L’anneau principal pourrait être constitué de poussières issues de la désagrégation d’anciens satellites ou de particules de surface arrachées par des forces de marées à des satellites encore existants. L’un des satellites naturels, Métis, est le plus proche de la planète et évolue en orbite circulaire autour d’elle. On le soupçonne d’alimenter l’anneau principal en particules qui seraient arrachées petit à petit de sa surface. Cet exercice vise à déterminer si des particules de surface peuvent être arrachées à Métis par les forces de marées de Jupiter pour alimenter l’anneau principal et si l’existence de Métis est menacée.
Données : – Rayon moyen de Jupiter : R = 69 911 km.
– Masse de Jupiter : M = 1,899 × 1027 kg.
– Masse volumique de Métis : rM = 860 kg·m–3 .
– Période de révolution de Métis : TM = 7 h 4 min 30 s.
– Constante de gravitation universelle : G = 6,67 × 10–11 m3 ·kg–1 ·s– 2 .
Partie A – Détermination du rayon r de l’orbite de Métis.
 L’étude du mouvement du satellite Métis, assimilé à un point matériel de masse m, est réalisée dans le référentiel lié au centre de Jupiter, appelé référentiel jovien, supposé galiléen. On note r le rayon de l’orbite circulaire de Métis autour de Jupiter. On étudie le mouvement de Métis dans le repère de Frenet.
1. Représenter sur un schéma Jupiter, Métis sur son orbite supposée circulaire et les vecteurs unitaires de ce repère.
2. Donner l’expression vectorielle de la force de gravitation F exercée par Jupiter sur Métis en fonction de G, M, m, r et du ou des vecteurs unitaires adaptés du repère de Frenet.
3. Représenter, sans souci d’échelle, cette force F sur le schéma de la question 1.

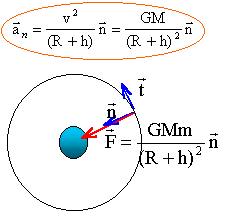
4. En appliquant la deuxième loi de Newton au satellite Métis en mouvement circulaire autour de Jupiter, montrer que ce mouvement circulaire de Métis est uniforme.
Selon l'axe de vecteur directeur n, la seconde loi de Newton conduit à :
GMm /(R+h)2 = mv2 / (R+h).
v2 = GM / (R+h) = constante.
Le mouvement est circulaire uniforme.
 5. Montrer que l’expression de la valeur de la vitesse du satellite Métis vaut v = ( G × M / r )½.
On pose r = R+h ; v2 = GM / (r)  : v = ( G × M / r )½.
 6. En déduire l’expression de la période de révolution T de Métis autour de Jupiter.
Métis décrit la circonférence 2pr à la vitesse v durant la période T.
2pr = vT = ( G × M / r )½ T.
T = 2pr / ( G × M / r )½ =2pr1,5 / ( G × M  )½

7. Retrouver la troisième loi de Kepler dans le cas d’un mouvement circulaire.
T = 2pr1,5 / ( G × M  )½.
T2=4p2 r3 / (GM)
T2 / r3 =4p2  / (GM).
 8. Montrer que le rayon r de l’orbite de Métis autour de Jupiter vaut 1,28 × 108 m.
T = 7 h 4 min 30 s=7*3600+4*60+30=2,547 104 s.
r3 =T2 GM / (4p2 ) =(2,547 104)2 x6,67 10-11 x1,899 1027 / (4x3,142)=2,08 1024 m3.
r =1,28 108 m.

... =  =
....
Partie B – Métis et les limites de Roche
Calculée pour la première fois par le mathématicien et astronome français Édouard Albert Roche en 1848, la limite de Roche est la distance assimilée au rayon de l’orbite en dessous de laquelle un petit corps céleste commencerait à se disloquer sous l'action des forces de marées causées par le corps céleste autour duquel il orbite. On distingue aujourd’hui deux limites de Roche :
– une limite de Roche « fluide » en-dessous de laquelle, en particulier, des satellites naturels peuvent encore orbiter. Cependant, ils perdent petit à petit de l’altitude en ralentissant, commencent à se déformer et à perdre de la matière en surface : leur fin de vie est programmée ;
 – une limite de Roche « rigide » en-dessous de laquelle aucun corps massif ne peut conserver sa structure sans être détruit, même un satellite. Dans le cas d’un satellite orbitant autour d’une planète, les formules permettant de calculer ces deux limites dans le cas de Jupiter et Métis sont les suivantes :

RJ est le rayon moyen de Jupiter, rJ la masse volumique de Jupiter et rM la masse volumique de Métis.
 9. Vérifier que la masse volumique de Jupiter est rJ = 1 327 kg·m–3 .
Volume de Jupiter : 4 / 3 p R3 =4 /3 x3,14 x(69 911 103)3=1,43 1024 m3.
M = 1,43 1024 rJ  ; rJ =1,899 1027 / (1,43 1024)=1 327 kg·m–3 .
 10. Calculer la limite de Roche « fluide » et la limite de Roche « rigide » pour Métis.
Dfluide =2,42 x69 911 103x(1 327 / 860)1/3=1,96 108 m.
Drigide =1,26 x69 911 103x(1 327 / 860)1/3=1,02 108 m.
11. En vous référant aux calculs de la partie A, prévoir, en justifiant, le destin de Métis.
Le rayon r de l’orbite de Métis autour de Jupiter vaut 1,28 × 108 m, valeur comprise entre la limite de Roche fluide et la limite de Roche rigide. Métis perd petit à petit de l'altitude en ralentissant ; il commence à se déformer et à perdre de la matière en surface. Sa fin de vie est programmée.





  
menu