La physique au service de l'aérogommage. Un bon liquide de refroidissement. Bac G, SI, Nouvelle Calédonie 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . .. .. ...... ... L’aérogommage consiste à projeter, grâce à de l’air sous pression, une poudre abrasive pour éliminer la peinture ou les salissures présentes sur la surface d’un matériau. Une fois l’opération terminée, la poudre utilisée est recyclée en la faisant passer à travers un tamis qui retient les déchets. Un tamis est un réseau plus ou moins serré de fils caractérisé par l’espace intermaille noté h . Pour simplifier, on suppose que toutes les particules solides considérées dans cet exercice sont sphériques. Celles qui peuvent passer au travers de la maille ont donc un diamètre inférieur à h. L’objectif de cet exercice est de déterminer la valeur de l’espace intermaille h d’un tamis disponible au laboratoire pour savoir s’il peut être utilisé. On réalise pour cela le dispositif expérimental présenté. Données : - diode laser de longueur d’onde  l= 650 nm ; - diamètre des fils du tamis testé : d = 0,20 mm ;  - l’expression de l’interfrange i (distance entre deux points brillants voisins) est donnée par la relation :i = l D / b. 1. Nommer le phénomène mis en évidence sur l’écran et préciser à quoi correspondent les zones sombres et brillantes. Interférences lumineuses. Interférences constructives : zones brillantes. Interférences destructives : zones sombres. On réalise une première expérience avec le tamis du laboratoire en plaçant l’écran à une distance D = 35 cm du tamis. La figure obtenue est alors trop petite pour pouvoir mesurer l’interfrange i. 2. Proposer, en la justifiant, une modification du dispositif expérimental permettant d’obtenir une figure plus grande, sans changer le matériel utilisé. i étant proportionnel à D, il suffit d'augmenter la distance tamis écran D. On refait l’expérience pour une distance D = 2,10 m. Les résultats obtenus après analyse par un logiciel de traitement d’image sont donnés. 3. À l’aide de la figure , montrer que l’interfrange vaut environ i = 1,6 mm en détaillant la méthode employée. 5 i =0,81 cm ; i =0,16 cm = 1,6 mm. 4. Déduire la valeur de b, puis la valeur de h à l’aide des données. i = l D / b ; b = l D / i =650 10-9 x 2,10 / (1,6 10-3) =8,5 10-4 m. h = b-d = 8,5 10-4 -2 10-4=6,5 10-4 m= 650 µm = 0,65 mm...  Pour nettoyer une surface dure, on utilise une poudre formée de grains de diamètre 500 µm. On suppose que le diamètre des déchets est d'au moins 1 mm. 5. Indiquer si ce tamis peut être utilisé pour le recyclage de cette poudre. Le diamètre des grains est inférieur  à h et la dimension des déchets est supérieure à h : le tamis peut être utilisé. ... =  = .... 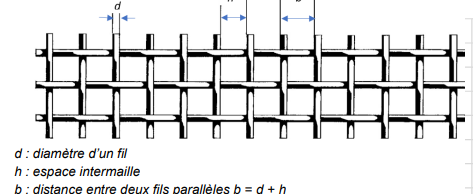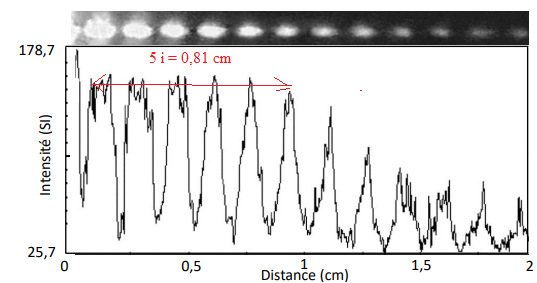Un bon liquide de refroidissement  Pour refroidir un moteur de voiture thermique, on utilise un liquide de refroidissement composé d’un mélange d’eau et d’éthylène glycol (éthane-1,2-diol), ce dernier jouant le rôle d’antigel. Dans cet exercice, on justifiera le choix d’un mélange commercial eau – éthylène glycol (respectivement 40 % - 60 % en volume) à l’aide de ses propriétés thermiques. Dans un premier temps, il est nécessaire de valider un protocole de mesure de la capacité thermique massique d’un liquide. 1 re partie : validation du protocole de mesure. On met en œuvre le protocole suivant avec de l’eau afin de valider la méthode de mesure de la capacité thermique massique d’un liquide.  - placer une masse m de liquide dans un calorimètre ;  - introduire la résistance chauffante dans le liquide ; - introduire un thermomètre dans le liquide et mesurer la température initiale Ti du système ; - alimenter la résistance chauffante en déclenchant le chronomètre à l’instant t = 0 s ; - relever la température T du liquide toutes les minutes tout en veillant à ce que l’intensité du courant I reste constante. Données : - L’énergie électrique Wélec(J) transférée par une résistance chauffante pendant la durée Dt(s) : Wélec = EIDt, avec E la tension en Volt entre les bornes du récepteur et I l’intensité du courant en Ampère qui le traverse ; - On rappelle l’expression de la variation de l’énergie interne U d’un système incompressible de masse m : DU = mcDT ; -  m = (550 ± 1) g de liquide ;  E = (5,73 ± 0,01) V ;  I = (0,97 ± 0,01) A ; - La valeur de référence pour la capacité thermique massique de l’eau est : cref = 4 181 J·°C-1 ·kg-1 . 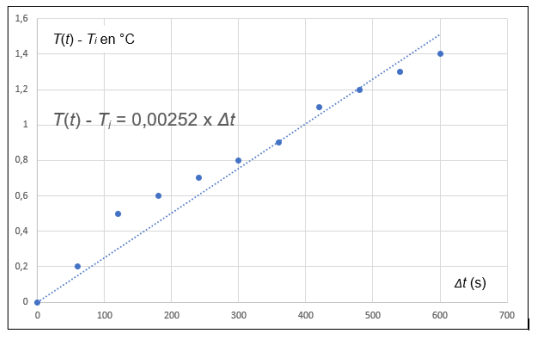Le graphique ci-dessous représente les résultats expérimentaux : Hypothèses : - La capacité thermique du calorimètre est négligée devant la capacité thermique des liquides introduits.  - On néglige tout phénomène de rayonnement. - Les échanges thermiques n’ont lieu qu’entre le liquide et la résistance chauffante. -  La résistance convertit intégralement l’énergie électrique Wélec qu’elle reçoit en transfert thermique Q, tel que Wélec = Q. - Le liquide est un fluide incompressible.  1. Nommer les deux modes de transfert thermiques intervenant dans le calorimètre. Convection et conduction. 2. Déduire du premier principe de la thermodynamique appliqué à ce liquide la relation : mceau(T(t) - Ti ) = EIDt Premier principe DU = W + Q avec W = 0 dans ce cas. Q = mceau(T(t) - Ti ) = Wélec = EIDt, 3. Montrer que la courbe ci-dessus est en accord approximatif avec l’expression : T(t) - Ti = keauDt 4. Exprimer keau en fonction de m, ceau, E et I à l’aide des questions précédentes. Les points expérimentaux sont à peu près alignés sur une droite passant par l'origine. keau =EI /(mceau) =5,73 x 0,97 /( 0,550 x4,18 103)~2,4 10-3 K s-1. La modélisation indiquée sur la courbe fournit la valeur de la constante keau. Son incertitude-type associée est : u(keau) = 1,8 x 10-4 SI. - L’incertitude sur la capacité thermique massique ceau se calcule avec :  u(ceau) = ceau [ ( u(keau)/keau ) 2 + ( u(E)/ E ) 2 + ( u(I) I ) 2]½. - Pour comparer le résultat d’une mesure mmes à une valeur de référence mref on utilise le quotient |mmes - mref| /u(m) , avec u(m) incertitude-type associée au résultat. Une mesure est validée quand ce quotient est inférieur à 2. 5. Calculer la valeur expérimentale de ceau et son incertitude-type associée. Conclure quant à la validité du protocole de mesure. ceau = EI / (m keau )=5,73 x0,97 / ( 0,550 x0,00252)=4,01 103 J kg-1 K-1. u(ceau) = 4,01 103 [ ( 1,8 10-4/0,00252 ) 2 + ( 0,01/ 5,73 ) 2 + ( 0,01 /0,97) 2]½~3 102 kg-1 K-1. |4,01 103-4181| / (3 102)=0,57  <2. Le protocole est valide. 2 e partie : justification du choix du liquide de refroidissement. Le liquide de refroidissement doit demeurer liquide aux températures extérieures d’utilisation. Il doit également absorber l’énergie thermique du moteur et la transférer au radiateur pour être évacuée vers l’extérieur. Il est ainsi d’autant plus efficace que sa capacité à stocker de l’énergie thermique lors d’une certaine variation de température est importante. En utilisant le protocole précédent, on a déterminé la capacité thermique massique du mélange. Le résultat est présenté dans le tableau ci-dessous ainsi que les données relatives à l’eau et à l’éthylène glycol. Ethylène glycol pur mélange eau 40 % éthylène glycol 60 % eau pure Capacité thermique massique 2400 3100 4180 Température de solidification -13 °C -37°C 0°C 6. Discuter l’intérêt d’utiliser le mélange eau-éthylène glycol par rapport aux deux liquides purs pour refroidir un moteur. La température de solidification  -37°C est très inférieure aux températures les plus froides de l'hiver. La capacité thermique massique reste très élevée.

menu