Exercice 3. 5 points.
On considère la fonction f définie pour tout réel x par :
f (x) = ln( exp(0,5 x) +2 )
On admet que la fonction f est dérivable sur R.
On considère la suite (u
n) définie par u
0 = ln(9) et, pour tout entier naturel n,
u
n+1 = f (u
n)
1. Montrer que la fonction f est strictement croissante sur R.
On pose u = exp(0,5x)+2 ; u' = 0,5 exp(0,5x)
f '(x) =u ' / u= 0,5 exp(0,5x) / ln(exp(0,5x)+2).
exp(0,5x ) >0 et ln(exp(0,5x)+2) >0 : f '(x) >0 ; f(x) est strictement croissante sur R.
2. Montrer que f (2ln(2)) = 2ln(2).
exp(0,5*2ln(2) =exp(ln(2)=2.
ln( exp(0,5 x) +2 )=ln(2+2) = ln(4) = ln(2
2) = 2 ln(2).
3. Montrer que u
1 = ln(5).
u
1 = ln(exp(0,5 u
0)+2)=ln(exp(0,5 ln(9))+2)=ln(exp(ln(9
0,5)+2)=ln(exp(ln(3))+2) =ln(3+2)=ln(5).
4. Montrer par récurrence que pour tout entier naturel n, on a :
2ln(2)
< u
n+1 < u
n.
Initialisation : 2 ln(2) = ln(4)
<ln(5)
<ln(9), la propriété est vraie au rang zéro.
Hérédité : la propriété est supposée vraie au rang n
2ln(2)
< u
n+1 < u
n.
f(x) étant strictement crpoissante sur R :
f(2ln(2))
< f(u
n+1 )
< f( u
n).
2 ln(2)
< u
n+2 < u
n+1.
La propriété est vraie au rang n+1
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n.
5. En déduire que la suite (u
n) converge.
La suite est strictement décroisante et minorée : donc d'après le théorème de convergence monotone, elle converge.
6. a. Résoudre dans R l’équation X
2 − X −2 = 0.
Discriminant : (-1)
2 -4x(-2) =9 = 3
2.
X
1 = (1-3) / 2 =
-1 ; X
2=(1+3) / 2 =
2.
b. En déduire l’ensemble des solutions sur R de l’équation :
e
x −e
0,5x −2 = 0
X = e
0,5 x >0 ; 2 = e
0,5x ;ln(2) = 0,5x ;
x = 2 ln(2).
c. En déduire l’ensemble des solutions sur R de l’équation f (x) = x.
ln( exp(0,5 x) +2 ) = x.
exp(0,5x)+2 = exp(x).
exp(x) -exp(0,5x) -2 =0.
Solution de cette équation x = 2 ln(2).
d. Déterminer la limite
l de la suite (u
n).
l vérifie f(
l) =
l.
l = 2 ln(2) d'après la question précédente.
Exercice 4. 5 points.
On considère la fonction f définie sur l’intervalle ]0 ; +∞[ par :
f (x) =
ln(x) /
x
2
+1.
On note C
f
la courbe représentative de la fonction f dans un repère orthonormé. On admet
que la fonction f est dérivable sur l’intervalle ]0 ; +∞[ et on note f
′
sa fonction dérivée.
1. Déterminer les limites de la fonction f en 0 et en +∞.
En déduire les éventuelles asymptotes à la courbe C
f
.
En 0
+ : ln(x) tend vers -oo ; ln(x) / x
2 tend vers -oo ; f(x) tend vers -oo.
La droite d'équation x =0 est asymptote.
En +oo :ln(x) et x
2 tendent vers +oo.
Par croissance comparée ln(x) / x
2 tend vers 0.
f(x) tend vers 1.
La droite d'équation y = 1 est asymptote.
2. Montrer que, pour tout réel x de l’intervalle ]0 ; +∞[, on a :
f
′
(x) =
(1−2ln(x)) /
x
3
.
On pose u = ln(x) et v = x
2.
u' = 1 /x ; v' = 2x.
(u'v-v'u) / v
2 =(x-2x ln(x)) / x
4 =(1-2ln(x) / x
3.
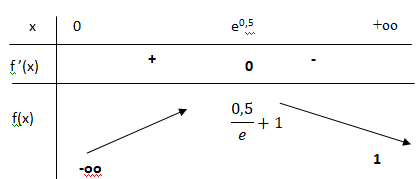
3. En déduire le tableau de variation de la fonction f sur l’intervalle ]0 ; +∞[.
f '(x) = 0 si ln(x) =0,5 ; x = e
0,5.
Si x < e
0,5, f '(x) >0 et f(x) est strictement croissante .
Si x > e
0,5, f '(x) <0 et f(x) est strictement décroissante .
 4. a.
4. a. Montrer que l’équation f (x) = 0 possède une unique solution, notée
a, sur l’intervalle ]0 ; +∞[.
Sur l'intervalle ]0 ; e
0,5], f est continue et strictement
croissante de -oo à 0,5 /e+1 > 1. D'après le corollaire du
théorème des valeurs intermédiaires, l'équation f(x) =0 admet une
solution unique
a.
Sur l'intervalle ] e
0,5, +oo[, f est continue et strictement décroissante de 0,5 /e+1 à 1. L'équation f(x) =0 n'admet aucune solution.
b. Donner un encadrement du réel
a d’amplitude 0,01.
La calculatrice donne : 0,65 <
a < 0,66.
c. En déduire le signe de la fonction f sur l’intervalle ]0 ; +∞[.
f(
a) =0.
f(x) <0 sur ]0 ;
a[ et f(x) >0 sur ]
a ; +oo[
5. On
considère la fonction g définie sur l’intervalle ]0 ; +∞[ par :
g(x) = ln(x).
On note Cg la courbe représentative de la fonction g dans un repère
orthonormé d’origine O. On considère un réel x strictement positif et
le point M de la courbe Cg d’abscisse x. On note OM la distance entre
les points O et M
.
a. Exprimer la quantité OM
2
en fonction du réel x.
On note H le projeté orthogonal de M sur l'axe des abscisses.
OM
2 =OH
2+HM
2= x
2 +(ln(x))
2.
b. Montrer que, lorsque le réel x parcourt l’intervalle ]0 ; +∞[, la quantité OM
2
admet un minimum en
a.
Soit la fonction h(x) = x
2 +(ln(x))
2.
h(x) est dérivable car somme de fonctions dérivables :
h '(x) = 2x +2 ln(x) / x= 2x(1+ ln(x) / x
2) = 2x f(x).
Sur ]0 ; +∞[ h'(x) possède le signe de f(x).
h'(x) <0 sur ]0 ;
a[ et positive sur [
a ; +oo[.
h admet un minimum en x =
a.
OM
2 admet un minimum en x=
a.
c. La valeur minimale de la distance OM, lorsque le réel x parcourt l’intervalle ]0 ; +∞[,
est appelée distance du point O à la courbe Cg . On note d cette distance.
Exprimer d à l’aide de
a.
Pour x =
a : OM
2 =
a2 +(ln(
a))
2.
f(
a) = 0 ;
ln(
a) /
a
2
+1=0.
ln(
a) = -
a2 ; (ln(
a) )
2=
a4 ;
OM
2 =
a2 +
a4=
a2 (1+
a2)
d étant la valeur minimale de POM : d =
a(1+
a2)
0,5.