Mathématiques, physique chimie. Bac STI2D 09 / 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . . .

.
.
.. ..
......


...
Une coulée comme Léon Marchand 4 points
  On appelle coulée la phase sous-marine qui suit le plongeon ou le virage d’un nageur.
Cet exercice présente une évaluation des forces de frottements auxquelles le nageur est soumis lors d’une coulée.
Partie 1
On suppose que le déplacement du nageur se produit à une profondeur constante lors de la coulée. Pendant cette phase, le sportif se laisse glisser dans l’eau, sans nager. Le mouvement du nageur est supposé rectiligne. Dans ces conditions, on peut
considérer que le nageur est uniquement soumis à la force résultante des forces de frottement de l’eau sur son corps, appelée traînée hydrodynamique et notée T. Cette force est de même direction que la vitesse du nageur, mais de sens opposé.
La figure  ci-après représente l’évolution de la vitesse du nageur en fonction du temps.

Q1. Indiquer en justifiant la réponse si le mouvement lors de la coulée du nageur est accéléré, décéléré, ou uniforme.
La vitesse diminue au cours du temps, le mouvement est décéléré.
Q2. Indiquer en justifiant la réponse si au cours de ce mouvement le travail de la force de traînée hydrodynamique T est positif, nul ou négatif.
L'énergie cinétique, donc l'énergie mécanique du nageur diminue du travail de la trainée. Le travail de cette force est donc négatif.
Donnée : masse du nageur m = 80 kg
Q3. Calculer la valeur de l’énergie cinétique du nageur aux instants t = 0 et t = 1,6 s.
v(t=0) = 3,6 m /s ; Ec(t=0) = ½mv2 =0,5 x80 x3,62=518,4 J.
v(t=1,6) = 1,4 m /s ; Ec(t=1,6) = ½mv2 =0,5 x80 x1,42=78,4 J.
On rappelle que la variation de l’énergie cinétique d’un système en mouvement entre deux instants est égale à la somme des travaux des forces extérieures qui lui sont appliquées lors de son déplacement.
Q4. En admettant que la seule force qui travaille est la force de traînée hydrodynamiqueT, calculer la valeur de son travail entre les instants t = 0 et t = 1,6 s.
78,4-518,4= -440 J.
Partie 2
On détermine un modèle numérique à partir de l’expérience de la partie 1. On suppose que la distance parcourue par le nageur durant la coulée, exprimée en mètre, en fonction du temps t, exprimée en seconde, est définie sur l’intervalle [0; 2] par :
f(t) = 3,64 ln (1 + t).
Q5. Calculer f(0).
f(0) = 3,64 ln(1) = 0.
Q6. On admet que la vitesse du nageur, en m/s, est donnée, en fonction du temps en s, par v(t)=3,64 / (1+t).
Montrer que l’accélération, correspondant à la dérivée de v est a(t) = -3,64 / (1+t)2.
a(t) = dv(t) / dt = -3,64 / (1+t)2.
Q7. Interpréter le signe de a dans le contexte de l’exercice et vérifier la cohérence avec l’observation de la courbe représentative de la fonction v.
L'accélération étant négative, le mouvement est donc décéléré.
Q8. Rappeler la relation entre le vecteur accélération  et la force de traînée hydrodynamique. Montrer que la modélisation effectuée est compatible avec une force de traînée de valeur proportionnelle au carré de la vitesse.

Sur un axe horizontal, orienté dans le sens du mouvement, cette relation conduit à :
T = -ma =80 x3,64 / (1+t)2=291,2 /(1+t)2= 291,2 /3,642 v2~22 v2.

Classe énergétique d’un logement. 5 points.
On souhaite étudier la possibilité d’améliorer la performance énergétique d’une habitation de classe énergétique B, en installant une pompe à chaleur géothermique.
Pour cette étude, on commence par calculer l’énergie électrique consommée annuellement pour le chauffage de l’habitation et pour la production d’eau chaude sanitaire.
Données :
- surface habitable de l’habitation : 80 m2 ;
- les murs de l’habitation sont composés de fibres de bois ;
- surface totale des murs : Smurs = 90 m2 ;
- conductivité thermique de la fibre de bois : l = 0,038 W·K−1·m−1 ;
- température à l’intérieur de la maison : Tint = 19°C ;
- température moyenne à l’extérieur de la maison en hiver : Text = 5°C ;
- durée annuelle d’utilisation du chauffage : 180 jours ;
- épaisseur des murs : e = 200 mm.
- La résistance thermique Rth d’une paroi d’épaisseur e, de surface S, constituée d’un matériau de conductivité thermique l est donnée par la relation :
Rth =e /(l S).
- Le flux thermique F à travers une paroi de résistance thermique Rth est proportionnel à la différence de température DT entre les deux côtés de la paroi selon la relation :
F =DT / Rth.
Énergie consommée pour chauffer l’habitation
Q1. Calculer la résistance thermique Rth,murs de la surface totale des murs de l’habitation.
Rth,murs =e /(l S).=0,200 / (0,038 x90)=0,0585 K W-1.
Q2. Calculer la valeur du flux thermique correspondant à la perte d’énergie au travers l’ensemble des murs.
F =DT / Rth= (Tint-Text) / Rth=14 / 0,0585~239 W.
Le flux thermique total perdu au travers de l’ensemble des limites de l’habitation, sols et plafonds inclus, a une valeur de 910 W. Ce flux thermique est égal au flux thermique que l’on doit fournir pour maintenir la température du logement à 19°C lorsque la température extérieure vaut 5°C.
Q3. Montrer que la résistance globale Rth,glob entre l’intérieur du logement et l’extérieur est voisine de 1,5 × 10−2 K·W−1.
Rth,glob =DT / F =14 / 910 =0,0154 ~1,5 × 10−2 K·W−1
Q4. Calculer, en wattheure (Wh), l’énergie thermique totale à fournir pour maintenir la température du logement à 19°C pendant la période de chauffage.
On rappelle que : 1 Wh = 3,6 × 103 J.
Flux(W) x durée (h)=910 x 24 x180 =3,9 106 Wh.

Énergie consommée pour chauffer l’eau chaude sanitaire
Le volume d’eau chaude consommé chaque jour dans le logement a une valeur V= 130 L.
Données :
- température de l’eau froide : q f = 15°C ;
- température de l’eau chaude : q c = 55°C ;
- masse volumique de l’eau : r = 1,00 kg·L−1 ;
- capacité thermique massique de l’eau : ceau = 4180 J·kg−1·K−1 ;
Q5. Montrer que l’énergie thermique Qeau nécessaire au chauffage de l’eau consommée sur une année, soit 365 jours, a pour valeur 2,2 × 106 Wh.
Qeau = V r Ceau( q c-q f)=130 x1,0 x4180 (55-15)=2,17 107 J ou 2,17 107 /3600=6,04 103 Wh
6,04 103 x365=2,2 × 106 Wh.
Q6. Montrer que l’énergie thermique totale consommée pour chauffer l’habitation et l’eau sanitaire pendant une année a une valeur voisine de 6,0 × 106 Wh.
 2,2 106 +3,9 106=6,1 × 106 Wh.

Apport de la pompe à chaleur
Une pompe à chaleur est un dispositif qui peut fournir à l’air intérieur de l’habitation une énergie thermique supérieure à l’énergie électrique consommée. Le coefficient de performance énergétique (COP) d’une pompe à chaleur correspond
au rapport entre l’énergie thermique restituée et l’énergie électrique consommée par celle-ci :
COP = Énergie thermique fournie par la pompe à chaleur / Énergie électrique consommée par la pompe à chaleur
Q7. Montrer que l’énergie électrique que consommerait une pompe à chaleur géothermique dont le COP vaut 4,0 pour chauffer annuellement l’habitation et l’eau sanitaire vaut environ 1,5 × 106 Wh.
6,1 × 106  / 4 =1,5 × 106 Wh.
Q8. En déduire la classe énergétique de l’habitation équipée de cette pompe à chaleur. Indiquer si la classe énergétique du logement est améliorée grâce à l’utilisation de cette pompe à chaleur.
 Sans pompe à chaleur : 6,1 106 / 80 =7,6 104 Wh m-2 = 76 kWh m-2. Classe B.
Avec pompe à chaleur :1,5 × 106  / surface habitable = 1,5 106 / 80 =.1,875 104 Wh m-2 ~19 kWh m-2. Clase A.
Q9. Proposer une autre solution permettant d’améliorer la classe énergétique du logement.
Isolation des murs ;  portes et fénètres équipées de double vitrage, isolation des combles.

... =  =
....
Exercice 3 4 points
Q1. On considère la fonction f définie sur R par f(x) =exp(-0,016x) -2 et on note f ' sa fonction dérivée.
f(0) = exp(0)-2 = 1-2 = -1.
 f '(x) = -0,016 exp(-0,016x).
f 'x) < 0 , f(x) est décroissante sur R. Réponse D.

Q2. Soit la fonction f définie sur [0 ; +∞[ par f(x) = 30 / (1+2x)
Est-il vrai que la valeur moyenne de f sur l’intervalle [5 ; 15] est supérieure à 3 ? Justifier la réponse.

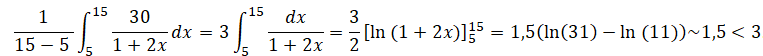Q3.
On note f(t) la température (en °C) d’un café en fonction du temps t (en minute) écoulé depuis sa sortie d’une machine à expresso. A l’instant t= 0, la température initiale du café est 83°C.
On admet que la fonction température est solution sur [0;+∞[ de l’équation différentielle : y ' = −0,08y + 1,84.
Déterminer l’expression de l’unique solution f qui vérifie les données précédentes.
Solution générale de y ' +0,08 y = 0.
f(t) = A exp(-0,08 t) avec A une constante réelle.
Solution particulière de l'équation différentielle : f(t) = 1,84 /0,08 =23.
Solution générale : f(t) = A exp(-0,08 t) +23.
f(0) =A+23 = 83 ; A = 60.
f(t) = 60 exp(-0,08 t) +23.

Q4.
On note f(t) la température (en °C) d’un café en fonction du temps t (en minute) écoulé depuis sa sortie d’une machine à expresso. On admet, pour tout t appartenant à  [0;+∞[, l’expression suivante : f(t) = 60exp(-0,08t) + 23.
Au bout de combien de temps la température du café sera-t-elle inférieure ou égale à 44°C ?
Donner la réponse à la minute près.
60exp(-0,08t) + 23 < 44.
60exp(-0,08t)  < 21.
exp(-0,08t) < 21 / 60.
-0,08t < ln(21 /60).
t > ln(60/ 21) / 0,08.
T >13,12 soit T > 14 min.


Exercice4. 7 points.
Puissance d’une installation
Les lave-linges constituent des postes de dépense énergétique et d’utilisation d’eau non négligeables. Cet exercice étudie la consommation électrique et la consommation d’eau liées à leur utilisation.
On rappelle que pour un courant alternatif sinusoïdal, les valeurs efficaces de la tension et de l’intensité du courant, Ueff et Ieff, sont reliées à leurs valeurs maximales, Umax et Imax, par les relations :
Ueff= Umax / 2½. Ieff= Imax / 2½..
Partie 1 – Moteur d’un lave-linge
On s’intéresse dans cette partie, à l’étude d’un moteur asynchrone qui équipe certains lave-linges. Pour simuler ce moteur, on utilise un moteur asynchrone de démonstration alimenté par un générateur de tension alternative.
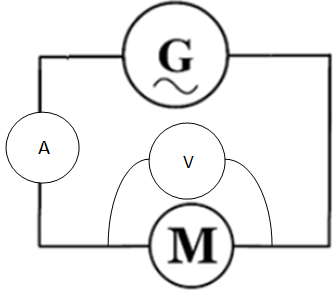
Q1. Recopier le schéma du circuit  et indiquer sur le schéma comment on doit connecter les appareils de mesure de l’intensité du courant électrique et de la tension aux bornes du moteur.

On a réalisé l’enregistrement de l’intensité du courant électrique et de la tension aux bornes du moteur en fonction du temps. Les courbes obtenues sont représentées sur la figure  ci-dessous.

Q2. Déterminer, en expliquant la méthode, la fréquence f de la tension u(t).
T = 0,02 s ; fréquence = 1 / T = 1 /0,02 = 50 Hz.
Q3. Déterminer les amplitudes Umax et Imax des signaux u(t) et i(t) et en déduire les valeurs efficaces correspondantes Ueff et Ieff.
Umax = 14 V ; Imax = 0,39 A.
Ueff = 14 / 1,414 ~9,9 V ; Ieff = 0,39 / 1,414 ~0,28 A.
Q4. Montrer la puissance apparente du moteur S a une valeur proche de 2,7 VA.
S = Ueff Ieff =9,9 x0,28~ 2,7 VA.
La puissance active P reçue par le moteur a pour valeur 1,93 W.
On rappelle que l’expression du facteur de puissance k en fonction de la puissance active et de la puissance apparente est : k = P / S
Q5. Calculer la valeur du facteur de puissance k pour le moteur.
k = 1,93 / 2,7 ~0,71.
Q6. Pour des raisons d’économie d’énergie dans les lignes de transport de l’énergie électrique, EDF impose à ses clients un facteur de puissance minimum de k = 0,93. Déterminer si le moteur étudié répond à cette obligation.
0,71 < 0,93, le moteur ne répond pas à cette obligation.

Partie 2 – Consommation d’eau d’un lave-linge
On mesure la puissance électrique consommée par un lave-linge, au cours d’un lavage à 30°C, à l’aide d’un wattmètre. La température initiale de l’eau admise dans le lave-linge est q1 = 20°C. Au cours du lavage les 3 phases suivantes sont répétées plusieurs
fois : pompage, chauffage et rotation du tambour.
Données :
- capacité thermique massique de l’eau : ceau = 4180 J·kg-1·K-1 ;
- masse volumique de l’eau : r = 1,0 kg·L−1 ;
- température initiale de l’eau : q1 = 20°C ;
- température finale de l’eau : q2 = 30°C.

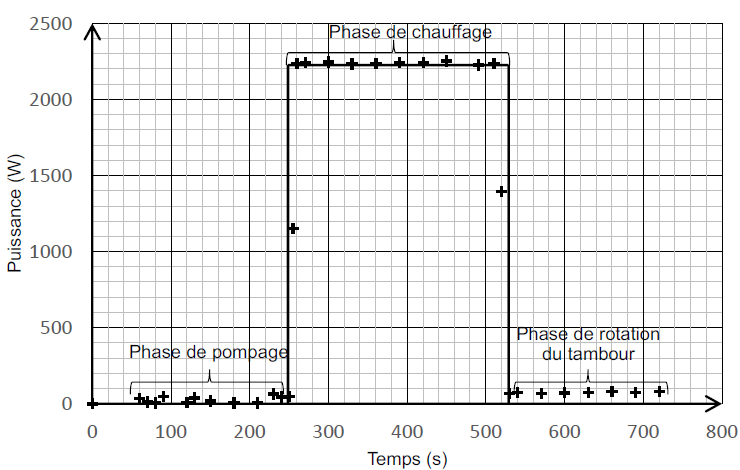
Q7. En utilisant la figure, déterminer l’énergie consommée lors de la phase de chauffage de l’eau. Vérifier que sa valeur est proche de E = 6,0 × 105 J.
P = 2200 W ; temps = 530-250=280 s.
E = 2200 x 280 ~6,0 105 J
Q8. En déduire la masse d’eau qui a été chauffée de 20°C à 30°C pendant cette phase, en admettant que toute l’énergie reçue pendant cette phase est utilisée pour chauffer l’eau.
E = m ceau (q2-q1) ; m = E / (ceau (q2-q1))=6 105 / (4180 x10)=14,35 ~ 14 kg.
Q9. Deux lavages et deux rinçages, qui consomment chacun la même masse d’eau, s’enchainent lors d’un cycle de lavage. En déduire le volume total d’eau consommé au cours d’un cycle de lavage et comparer cette valeur au volume de 52 L indiqué par le constructeur.
14 x4 = 56 L d'eau, valeur supérieure de 7 % par rapport à la valeur constructeur.

Partie 3 – Détartrage d’un lave-linge et économie d’énergie
Les dépôts de tartre sur les résistances des lave-linges augmentent leur consommation électrique, car le tartre est un mauvais conducteur thermique. Une résistance recouverte de tartre entraîne une surconsommation électrique estimée, selon les fabricants, entre 10 et 20 %. Le détartrage de la résistance permet donc de réduire la consommation énergétique et de prolonger la durée de vie de la machine.
Le tartre est formé de carbonate de calcium, de formule chimique CaCO3. On utilise une solution d’acide chlorhydrique (HCl) comme détartrant.
Données :
- équation chimique de la réaction entre le carbonate de calcium et l'acide chlorhydrique :
CaCO3(s) + 2 HCl(aq) → CaCl2(aq) + H2O(l) + CO2(g)
- masse molaire du carbonate de calcium : M(CaCO3) = 100,1 g/mol ;
- masse molaire de l'acide chlorhydrique : M(HCl) = 36,5 g/mol ;
- masse volumique d’une solution d'acide chlorhydrique commerciale :
r = 1,18 g·mL-1 ;
- concentration massique en HCl d’une solution d’acide chlorhydrique commerciale cm = 23,0 g·L-1.
Q10. La résistance d'un lave-linge est recouverte de 25,0 g de tartre. En supposant que tout le carbonate de calcium réagit avec l'acide chlorhydrique, calculer la masse d'acide chlorhydrique nécessaire pour éliminer tout le tartre. Comparer cette masse à
celle contenue dans 100 mL de solution commerciale d'acide chlorhydrique.
Quantité de matière de tatre n=25,0 / M(CaCO3) = 25,0 / 100,1 ~0,25 mol.
Quantité de matière d'acide chlorhydrique : 2 n = 0,50 mol.
masse d'acide : 0,50 xM(HCl) = 0,50 x36,5 =18,25 ~18 g.
Masse de 100 mL d'acide chmorhydrique : 100 x1,18 = 118 g.
18 / 118 ~0,15 ( 15 %).

En l’absence de tartre, la machine consomme 2,0 kWh par cycle de lavage. La couche de tartre augmente la consommation électrique de 20%.
Q11. Calculer l’énergie économisée par le détartrage d’une machine entartrée, pour 100 cycles de lavages.
2,0 x0,20=0,4 kWh par cycle.
0,4 x100 = 40 kWh.
Donnée : coût de l’électricité : 0,25 € / kWh.
40 x0,25 =10 €.
Q12. Discuter des avantages environnementaux et économiques du détartrage régulier des appareils électroménagers.
Economie d'énergie ; prévention des pannes due au tartre ;
L'acide chlorhydrique est dangereux et finit dans les eaux usées.





  
menu