Mathématiques, Physique Bac STI2D, Nouvelle Calédonie 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . .. .. ...... ... Condition d’utilisation d’un médicament. 4 points. Le 177Lu-PSMA est un médicament radiopharmaceutique indiqué dans le traitement de certaines tumeurs. Il est composé de lutécium 177 (177Lu) qui est un isotope radioactif du lutécium et qui se désintègre par émission ß − en hafnium 177 (177Hf ). Lors de la mise en œuvre de certains traitements, ce médicament se fixe sur des récepteurs présents à la surface de la tumeur et émet des rayonnements qui vont détruire les cellules malignes. 1. Nommer les différents types de rayonnement radioactif. Rayonnements alpha, béta+, béta- et gamma. 2. Préciser la nature de la particule produite lors de la désintégration du lutécium 177 en hafnium 177. 17771Lu -->  17772Hf +0-1e. (électron). 3. Définir l’activité d’une source radioactive. L'activité radioactive est le nombre de désintégrations par seconde.  Le document suivant décrit l’évolution au cours du temps de l’activité du lutécium présent dans le médicament injecté au patient. 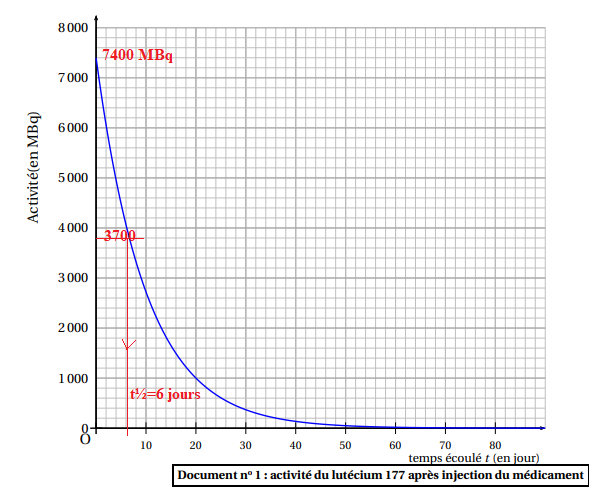4. Déterminer l’activité initiale de l’échantillon injecté au patient. 7400 MBq.  5. Rappeler la définition de la demi-vie d’une espèce radioactive. Durée au bout de laquelle l'activité initiale est divisée par 2. 6. Déterminer graphiquement la demi-vie du lutécium 177 en faisant apparaître les traits de construction.  t½ = 6 jours.  On admet que la fonction A qui modélise l’évolution de l’activité radioactive (en MBq) du lutécium 177 contenu dans une dose de ce médicament, en fonction du temps t, exprimé en jour écoulé depuis l’injection, vérifie l’équation différentielle : y ′ = −0,1y où y est une fonction définie et dérivable sur l’intervalle [0;+∞[ et y ′ sa dérivée. 7. Démontrer, en admettant que A(0) = 7400, que, pour tout réel t positif ou nul, on a : A(t) = 7400 e −0,1t . Solution générale de y'+0,1 y =0 : A(t) = B exp(-0,1t) avec B une constante réelle. A(0) =B = 7400. A(t) = 7400 exp(-0,1t). L’activité radioactive du lutécium 177 est considérée comme négligeable et sans risque pour l’environnement lorsqu’elle a perdu plus de 99,9 % de sa valeur initiale. 8. Montrer que l’activité du lutécium 177 contenu dans cette dose de médicament a diminué de plus de 99,9 % au bout de 70 jours. 7400 x(1-0,999) =7,4 MBq. A(70) = 7400 exp(-7)=6,75  < 7,4.. Le fabricant du médicament indique dans une notice : « Stocker dans un sac en plastique tous les objets non lavables contenant des traces d’urine et placer le sac dans une poubelle à l’écart. Le jeter aux ordures ménagères au bout de 70 jours ». 9. Commenter, en utilisant le résultat de la question précédente, la préconisation du fabricant. Au bout de 70 jours, l’activité radioactive du lutécium 177 est considérée comme négligeable et sans risque pour l’environnement ayant perdu plus de 99,9 % de sa valeur initiale. ... =  = .... EXERCICE 3 (4 points)  Partie I Dans un repère orthogonal d’origine O, on considère les points A(0; 12), B(1; 12) et C(1; 0). Dans la figure ci-dessous, deux courbes C1 et C2 délimitent un domaine grisé D1, un domaine hachuré D2, et un domaine D3 non coloré, à l’intérieur du rectangle OABC. La courbe C2 est la représentation graphique de la fonction f définie sur l’intervalle [0;1] par : f (x) = 6x 3 +6x 2 1. Calculer l’intégrale  Primitive de f(x) : F(x) = 6 x4 /4 +6 x3 /3=1,5 x4 +2x3. F(1) =1,5+2=3,5. F(0)+0 ; F(1)-F(0) = 3,5 On admet que la fonction f est positive sur l’intervalle [0; 1]. 2. Interpréter le résultat du calcul précédent dans le contexte de l’exercice. L'aire du domaine D1 est égale à 3,5 unités d'aire. L’aire du domaine D2 hachuré a été calculée (en unité d’aire) à l’aide d’un logiciel et vaut 135 / 32.  3. Estimer l’aire en unité d’aire du domaine D3. Aire du rectangle ABCO : 1 x12 = 12 unités d'aire. Aire du domaine D3 : 12 -135 /32 -3,5=8,5-135 /32=(272-135 ) /32 = 137 / 32 unités d'aire. Partie II On considère les nombres complexes z1 = 1 − i 3½ et z2 = 4 exp( i p /6) où i désigne le nombre complexe de module 1 et d’argument p/2 .  4. Écrire le nombre z1 sous forme exponentielle. Détailler les calculs. Module de z1 : (12+3)½ =2. z1 / 2 =0,5 -i 3½ /2 = cos (-p/3) +i sin(-p/3)= exp(-ip/3). z1 = 2 exp(-ip/3). 5. Démontrer que le nombre Z = z12 × z2, est un nombre imaginaire pur en détaillant les calculs. Z =22 exp(-2ip/3) x4 exp( i p /6) = 16 exp( i (p/6-2p/3))=.16 exp( i (p/6-4p/6))= 16 exp(-i p/2).

menu