Cargo dirigeable. Bac G Amérique du Sud 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . .. .. ...... ... Exercice 3 5 points Pour transporter des charges lourdes certaines startups travaillent sur des projets de ballons cargos dirigeables. Ces « grues volantes » permettraient d’embarquer ou de livrer des charges dans des zones peu accessibles. Grâce à un gaz porteur moins dense que l’air, un dirigeable peut voler de manière beaucoup plus économe en carburant qu’un hélicoptère ou un avion. L’objectif de cet exercice est de vérifier la charge maximale embarquable dans un dirigeable et d’étudier un système permettant d’effectuer un chargement en vol stationnaire. Caractéristiques du dirigeable étudié : - volume du dirigeable : 𝑉 = 180 000 m3 ; - masse du dirigeable avant remplissage en gaz porteur : md = 65 tonnes. Partie 1. Étude de la charge maximale embarquée Données : − masse molaire de l’hélium : MHe = 4,0 g⋅mol -1 ; − constante des gaz parfaits :R = 8,314 J·K -1 ·mol -1 ; − conversion entre les échelles de température : T(K) = q(°C) + 273 ; − 1,0 bar = 1,0 × 105 Pa ;  − intensité de la pesanteur : 𝑔 = 9,8 m∙s -2 . On fait l’hypothèse que le dirigeable a été entièrement rempli d’hélium, se comportant comme un gaz parfait, sous une pression de 𝑃 = 1,1 bar et à la température q = 25 °C. Q1. Montrer que la valeur de la masse d’hélium embarqué dans le dirigeable est proche de mHe = 32 tonnes. Quantité de matièe d'héliumn = V / 22,4 = 1,8 108/22,4=8,0 106 mol. Masse d'hélium : n MHe = 8,0 106 x4 =3,2 107 g = 32 tonnes. Q2. Parmi les relations suivantes, choisir, en justifiant, celle donnant l’expression vectorielle de la poussée d’Archimède  exercée par l’air sur le dirigeable. Poussée verticale dirigée vers le haut. Q3. Calculer la valeur de la poussée d’Archimède exercée par l’air sur le dirigeable à une altitude de 3000 m. Pa =0,88 x 180 000 x9,8=1,55 106 N ~1,6 106 N. Q4. Préciser comment l’intensité de cette force évolue en fonction de l’altitude. La masse volumique de l'air diminue avec l'altitude ; la poussée d'Archimède diminue avec l'altitude. On étudie le système {dirigeable} dans le référentiel terrestre supposé Galiléen. Q5. À l’aide d’une des lois de Newton que l’on citera, déterminer la relation entre le poids  du système et la poussée d’Archimède  qu’il subit lorsqu’il vole en ligne droite, à altitude et vitesse constante. Selon un axe vertical orienté vers le haut, la seconde loi de Newton conduit à : -mg + rair Vg = 0 Q6. Vérifier que la charge maximale transportable par ce dirigeable à 3000 m d’altitude est proche de 60 tonnes. Masse totale = 65+32 + mcharge = 97+mcharge en tonnes Poussée = 1,6 106 N. Masse totale = 1,6 106 /9,8=1,6 105 kg ou 160 tonnes.  mcharge  = 160-97 ~60 tonnes. ... =  = .... Chargement d'un tronc d'arbre  Un des défis à résoudre pour le transport de charge lourde est de pouvoir charger ou décharger le dirigeable en vol stationnaire, en quelques minutes. Une des solutions technologiques envisagée est un transfert d’eau. À son départ, le dirigeable possède un réservoir rempli d’eau. Pour embarquer la charge en vol stationnaire, le dirigeable vide son réservoir d’une masse d’eau équivalente à la masse de la charge afin de rester fixe par rapport au sol. 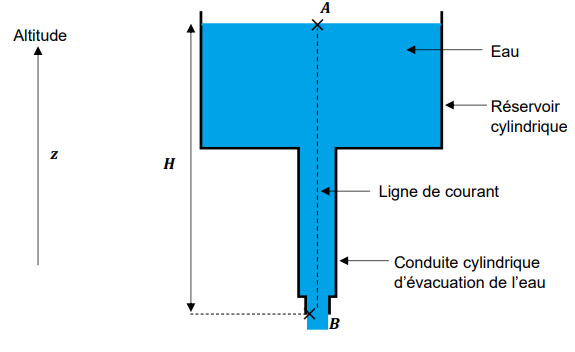Données :  − diamètre du réservoir en 𝐴 : dA = 3,0 m ; − diamètre du conduit au niveau de la sortie d’eau en 𝐵 : dB = 15 cm ; − masse volumique de l’eau : r = 1000 kg∙m-3 ; − hauteur 𝐻 entre les points A et B : 𝐻 = 30 m ; − l’écoulement d’un fluide incompressible en régime permanent peut être modélisé par la relation de Bernoulli. Sur une ligne de courant : P+½r v2 +r g z = constante , avec P la pression du fluide (en Pa), r la masse volumique du fluide (en kg∙m-3 ), v la vitesse d’écoulement du fluide (en m∙s -1 ) et z l’altitude (en m) ; − dans une conduite, la relation entre le débit volumique DV (en m3 ∙s -1 ), la vitesse d’écoulement v (en m∙s -1 ) d’un fluide incompressible en régime permanent et S l’aire de la section du conduit (en m2) est donnée par : DV = v S. L’eau sera considérée comme un fluide incompressible, son écoulement s’effectue en régime permanent. Q7. En exploitant la conservation du débit volumique, montrer que la vitesse d’écoulement vA au point A est négligeable par rapport à la vitesse d’écoulement vB au point B. vA SA= vB SB. vA = vB SB /SA =vB (dB / dA)2=vB (0,15 / 3,0)2=2,5 10-3 vB. Q8. En appliquant la relation de Bernoulli sur la ligne de courant entre les points A et B et sachant que les pressions du fluide en A et B sont égales à la pression atmosphérique, montrer que la vitesse d’écoulement vB du fluide en B est donnée par l’expression : vB2 =2gH. ½r vA2 +r g zA = ½r vB2 +r g zB ; ½vA2 +g zA = ½ vB2 + g zB ; g zA ~ ½ vB2 + g zB ; vB2 ~2g(zA-zB) ~2gH.   On envisage la charge d’un morceau de bois de mbois = 8 tonnes. Q9. Déterminer la durée minimale nécessaire pour la vidange de l’eau nécessaire au chargement de ce morceau de bois dans le dirigeable. Commenter le résultat obtenu. Volume d'eau à vider : 8 m3. vB =(2x9,8 x30)½=24,2 m /s. Section en B : 3,14 x(0,15/2)2=1,77 10-2 m2. Débit en B : 24,2 x1,77 10-2~0,43 m3 /s. Durée de la vidange : 8 / 0,43 ~19 s, c'est assez rapide.

menu